16.5: Central projection

Last updated
Save as PDF

Page ID: 23686

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The central projection is analogous to the projective model of hyperbolic plane which is discussed in Chapter 17.

Let $\Sigma$ be the unit sphere centered at the origin which will be denoted by $O$. Suppose that $\Pi^+$ denotes the plane defined by the equation $z=1$. This plane is parallel to the $xy$-plane and it passes thru the north pole $N =(0,0,1)$ of $\Sigma$.

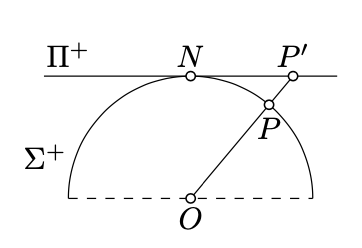
$截屏2021-03-01 上午10.34.45.png$

Recall that the northern hemisphere of $\Sigma$, is the subset of points $(x,y,z)\in \Sigma$ such that $z>0$. The northern hemisphere will be denoted by $\Sigma^+$.

Given a point $P\in \Sigma^+$, consider the half-line $[OP)$. Suppose that $P'$ denotes the intersection of $[OP)$ and $\Pi^+$. Note that if $P=(x,y,z)$, then $P'=(\dfrac{x}{z},\dfrac{y}{z},1)$. It follows that $P\leftrightarrow P'$ is a bijection between $\Sigma^+$ and $\Pi^+$.

The described bijection $\Sigma^+ \leftrightarrow \Pi^+$ is called the central projection of the hemisphere $\Sigma^+$.

Note that the central projection sends the intersections of the great circles with $\Sigma^+$ to the lines in $\Pi^+$. The latter follows since the great circles are intersections of $\Sigma$ with planes passing thru the origin as well as the lines in $\Pi^+$ are the intersection of $\Pi^+$ with these planes.

The following exercise is analogous to Exercise 17.2.1 in hyperbolic geometry.

Exercise $\PageIndex{1}$

Let $\triangle_sABC$ be a nondegenerate spherical triangle. Assume that the plane $\Pi^+$ is parallel to the plane passing thru $A$, $B$, and $C$. Let $A'$, $B'$, and $C'$ denote the central projections of $A$, $B$ and $C$.

Show that the midpoints of $[A'B']$, $[B'C']$, and $[C'A']$ are central projections of the midpoints of $[AB]_s$, $[BC]_s$, and $[CA]_s$ respectively.
Use part (a) to show that the medians of a spherical triangle intersect at one point.

Hint

(a). Observe and use that $OA' = OB' = OC'$.

(b). Note that the medians of spherical triangle ABC map to the medians of Euclidean a triangle $A'B'C'$. It remains to apply Theorem 8.3.1 for $\triangle A'B'C'$.