18.4: Euler's formula
- Page ID
- 23699
Let \(\alpha\) be a real number. The following identity is called Euler’s formula:
\[e^{i\cdot\alpha}=\cos\alpha+i\cdot\sin\alpha.\]
In particular, \(e^{i\cdot\pi}=-1\) and \(e^{i\cdot\frac\pi2}=i\).
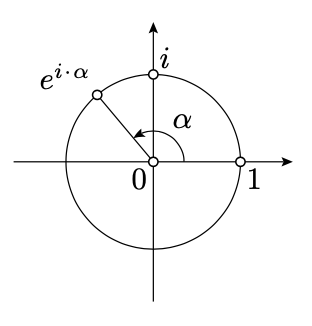
Geometrically, Euler’s formula means the following: Assume that \(O\) and \(E\) are the points with complex coordinates \(0\) and \(1\) respectively. Assume
\(OZ=1\quad \text{and}\quad \measuredangle EOZ \equiv \alpha,\)
then \(e^{i\cdot\alpha}\) is the complex coordinate of \(Z\). In particular, the complex coordinate of any point on the unit circle centered at \(O\) can be uniquely expressed as \(e^{i\cdot\alpha}\) for some \(\alpha\in(-\pi,\pi]\).
The proof of Euler’s identity depends on the way you define the exponential function. If you never had to apply the exponential function to an imaginary number, you may take the right hand side in 18.4.1 as the definition of the \(e^{i\cdot\alpha}\).
In this case, formally nothing has to be proved, but it is better to check that \(e^{i\cdot\alpha}\) satisfies familiar identities. Mainly,
\(e^{i\cdot \alpha}\cdot e^{i\cdot \beta}= e^{i\cdot(\alpha+\beta)}.\)
The latter can be proved using 18.1.2 and the following trigonometric formulas, which we assume to be known:
\(\begin{aligned} \cos(\alpha+\beta)&=\cos\alpha\cdot\cos\beta-\sin\alpha\cdot\sin\beta, \\ \sin(\alpha+\beta)&=\sin\alpha\cdot\cos\beta+\cos\alpha\cdot\sin\beta.\end{aligned}\)
If you know the power series for the sine, cosine, and exponential function, then the following might convince that the identity 18.4.1 holds:
\(\begin{aligned} e^{i\cdot \alpha } &{}= 1 + i\cdot \alpha + \frac{(i\cdot \alpha )^2}{2!} + \frac{(i\cdot \alpha )^3}{3!} + \frac{(i\cdot \alpha )^4}{4!} + \frac{(i\cdot \alpha )^5}{5!} + \cdots = \\ &= 1 + i\cdot \alpha - \frac{\alpha ^2}{2!} - i\cdot\frac{ \alpha ^3}{3!} + \frac{\alpha ^4}{4!} + i\cdot\frac{ \alpha ^5}{5!} - \cdots = \\ &= \left( 1 - \frac{\alpha ^2}{2!} + \frac{\alpha ^4}{4!} - \cdots \right) + i\cdot\left( \alpha - \frac{\alpha ^3}{3!} + \frac{\alpha ^5}{5!} - \cdots \right) = \\ &= \cos \alpha + i\cdot\sin \alpha.\end{aligned}\)


