18.6: Method of complex coordinates
- Page ID
- 23701
The following problem illustrates the method of complex coordinates.
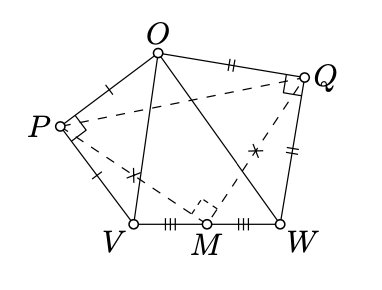
Let \(\triangle OPV\) and \(\triangle OQW\) be isosceles right triangles such that
\(\measuredangle VPO = \measuredangle OQW=\dfrac{\pi}{2}\)
and \(M\) be the midpoint of \([VW]\). Assume \(P\), \(Q\), and \(M\) are distinct points. Show that \(\triangle PMQ\) is an isosceles right triangle.
- Solution
-
Choose the complex coordinates so that \(O\) is the origin; denote by \(v, w, p, q, m\) the complex coordinates of the remaining points respectively.
Since \(\triangle OPV\) and \(\triangle OQW\) are isosceles and \(\measuredangle VPO=\measuredangle OQW=\dfrac{\pi}{2}\), 18.3.2 and 18.5.1 imply that
\(\begin{aligned} v-p&=i\cdot p, & q-w&=i\cdot q.\end{aligned}\)
Therefore
\(\begin{aligned} m&=\tfrac12\cdot(v+w)= \\ &=\tfrac{1+i}2\cdot p+\tfrac{1-i}2\cdot q.\end{aligned}\)
By a straightforward computations, we get that
\(p-m=i\cdot (q-m).\)
In particular, \(|p-m|=|q-m|\) and \(\arg\dfrac{p-m}{q-m}=\dfrac{\pi}{2}\); that is, \(PM=QM\) and \(\measuredangle QMP =\dfrac{\pi}{2}\).
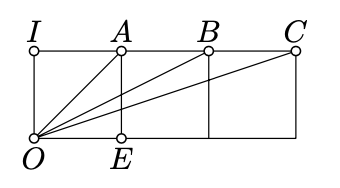
Consider three squares with common sides as on the diagram. Use the method of complex coordinates to show that
\(\measuredangle EOA+\measuredangle EOB+\measuredangle EOC=\pm\dfrac{\pi}{2}.\)
- Hint
-
We can choose the complex coordinates so that the points \(O, E, A, B\), and \(C\) have coordinates \(0, 1, 1 + i, 2 + i\), and \(3 + i\) respectively.
Set \(\measuredangle EOA = \alpha\), \(\measuredangle EOB = \beta\), and \(\measuredangle EOC = \gamma\). Note that
\(\begin{array} {rcl} {\alpha + \beta + \gamma} & \equiv & {\arg (1 + i) + \arg (2 + i) + \arg (3 + i) \equiv} \\ {} & \equiv & {\arg [(1 + i) \cdot (2 + i) \cdot (3 + i)] \equiv \arg [10 \cdot i] = \dfrac{\pi}{2}} \end{array}\)
Note that these three angles are acute and conclude that \(\alpha + \beta + \gamma = \dfrac{\pi}{2}\).
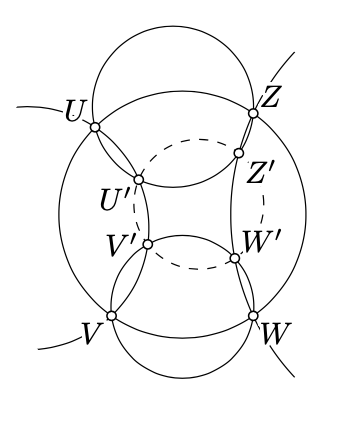
Check the following identity with six complex cross ratios:
\((u,w;v,z)\cdot(u',w';v',z')=\frac{(v,w';v',w)\cdot(z,u';z',u)}{(u,v';u',v)\cdot(w,z';w',z)}.\)
Use it together with Theorem 18.5.1 to prove that if \(\square UVWZ\), \(\square UVV'U'\), \(\square VWW'V'\), \(\square WZZ'W'\), and \(\square ZUU'Z'\) are inscribed, then \(\square U'V'W'Z'\) is inscribed as well.
- Hint
-
The identity can be checked by straightforward computations.
By Theorem 18.5.1, five from six cross ratios in the this identity are real. Therefore so is the sixth cross ratio; it remains to apply the theorem again.
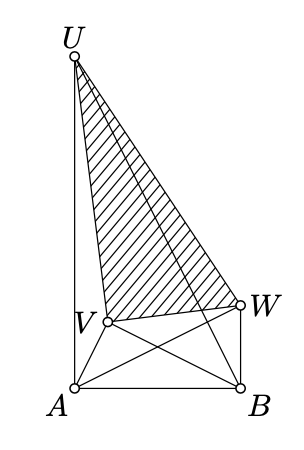
Suppose that points \(U\), \(V\) and \(W\) lie on one side of line \((AB)\) and \(\triangle UAB\sim \triangle BVA \sim \triangle ABW\). Denote by \(a\), \(b\), \(u\), \(v\), and \(w\) the complex coordinates of \(A\), \(B\), \(U\), \(V\), and \(W\) respectively.
- Show that \(\dfrac{u-a}{b-a}=\dfrac{b-v}{a-v}=\dfrac{a-b}{w-b}=\dfrac{u-v}{w-v}\).
- Conclude that \(\triangle UAB\sim \triangle BVA \sim \triangle ABW\sim \triangle UVW\).
- Hint
-
Use 3.7 and 3.10 to show that \(\angle UAB, \angle BVA\), and \(\angle ABW\) have the same sign. Note that by SAS we have that
\(\dfrac{AU}{AB} = \dfrac{VB}{VA} = \dfrac{BA}{BW}\) and \(\measuredangle UAB = \measuredangle BVA =\measuredangle ABW.\)
The later means that \(|\dfrac{u - a}{b - a}| = |\dfrac{b - v}{a - v}| = |\dfrac{a - b}{w - b}|\), and \(\arg \dfrac{b - a}{u - a} = \arg \dfrac{a - b}{w - b}\). It implies the first two equalities in
\[\dfrac{b - a}{u - a} = \dfrac{a - v}{b - v} = \dfrac{w - b}{a -b} = \dfrac{w - v}{u - v}.\]
the last equality holds since
\(\dfrac{(b - a) + (a -v) + (w - b)}{(u - a) + (b - v) + (a -b)} = \dfrac{w - v}{u - v}.\)
To prove (b), rewrite 18.6.1 using angles and distances between the points and apply SAS.


