19.1: Classical problems
- Page ID
- 23703
In this section we list a couple of classical construction problems; each known for more than a thousand years.
The solutions of the following two problems are quite nontrivial.
Construct an inscribed quadrangle with given sides.
Construct a circle that is tangent to three given circles.
Several solutions of this problem based on different ideas are presented in [9]. The following exercise is a simplified version of the problem of Apollonius, which is still nontrivial.
Construct a circle that passes thru a given point and is tangent to two intersecting lines.
- Hint
-
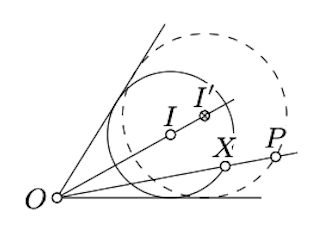
Let \(O\) be the point of intersection of the lines. Construct a circle \(\Gamma\), tangent to both lines, the crosses \([OP)\); denote its center by \(I\). Suppose that \(X\) denotes one of the points of intersections of \(\Gamma\) and \([OP)\).
Construct a point \(I' \in [OI)\) such that \(\dfrac{OI'}{OI} = \dfrac{OP}{OX}\). Observe that the circle passing thru \(P\) and centered at \(I'\) is a solution.
The following three problems cannot be solved in principle; that is, the needed compass-and-ruler construction does not exist.
Construct the side of a new cube that has the volum tice as big as the volume of a given cube.
In other words, given a segment of the length \(a\), one needs to construct a segment of length \(\sqrt[3]{2}\cdot a\).
Construct a square with the same area as a given circle.
If \(r\) is the radius of the given circle, we need to construct a segment of length \(\sqrt{\pi}\cdot r\).
In fact, there is no compass-and-ruler construction that trisects angle with measure \(\dfrac{\pi}{3}\). Existence of such a construction would imply constructability of a regular 9-gon which is prohibited by the following famous result:
A regular \(n\)-gon inscribed in a circle with center \(O\) is a sequence of points \(A_1\dots A_n\) on the circle such that
\(\measuredangle A_nOA_1=\measuredangle A_1OA_2=\dots=\measuredangle A_{n-1}OA_n=\pm\tfrac2n\cdot \pi.\)
The points \(A_1,\dots, A_n\) are vertexes, the segments \([A_1A_2], \dots, [A_nA_1]\) are sides and the remaining segments \([A_iA_j]\) are diagonals of the \(n\)-gon.
A construction of a regular \(n\)-gon, therefore, is reduced to the construction of an angle with size \(\tfrac2n\cdot \pi\).
A regular \(n\)-gon can be constructed with a ruler and a compass if and only if \(n\) is the product of a power of \(2\) and any number of distinct Fermat primes.
A Fermat prime is a prime number of the form \(2^k+1\) for some integer \(k\). Only five Fermat primes are known today:
3, 5, 17, 257, 65537.
For example,
- one can construct a regular 340-gon since \(340=2^2\cdot 5\cdot 17\) and \(5\) as well as \(17\) are Fermat primes;
- one cannot construct a regular 7-gon since \(7\) is not a Fermat prime;
- one cannot construct a regular 9-gon; altho \(9=3\cdot 3\) is a product of two Fermat primes, these primes are not distinct.
The impossibility of these constructions was proved only in the 19th century. The method used in the proofs is indicated in the next section.


