19.4: Verifications
- Page ID
- 23706
Suppose we need to verify that a given configuration is defined by a certain property. Is it possible to do this task by a geometric construction with given tools? We assume that we can verify that two constructed points coincide.
Evidently if a configuration is constructible, then it is verifiable — simply repeat the construction and check if the result is the same. Some nonconstuctable configuration can be verifiable. For example, it does not pose a problem to verify that the given angle is trisected while it is impossible to trisect a given angle with ruler and compass. A regular 7-gon provides another example of that type — it is easy to verify, while Gauss–Wantzel theorem states that it is impossible to construct with ruler and compass.
Since we did not prove the impossibility of angle trisection and Gauss–Wantzel theorem, the following example might be more satisfactory. It is based on Exercise 19.3.2 which states that it is impossible to construct an equilateral with set-square only.
Make a set-square construction verifying that a given triangle is equilateral.
- Hint
-
Observe that three perpendiculars on the diagram meet at one point if and only if the triangle is isosceles. Use this observation couple of times to verify that the given triangle is equilateral.
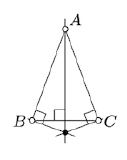
This observation leads to a source of impossible constructions in a stronger sense — those that are not even not verifiable.
The following example is closely related to Exercise 10.3.2. Recall that a circumtool produces a circle passing thru any given three points or a line if all three points lie on one line.
Show that with a circumtool only, it is impossible to verify that a given point is the center of a given circle \(\Gamma\). In particular it is impossible to construct the center with a circumtool only.
In geometric constructions, we allow to choose some free points, say any point on the plane, or a point on a constructed line, or a point that does not lie on a constructed line, or a point on a given line that does not lie on a given circle, and so on.
In principle, when you make such a free choice it is possible to make a right construction by accident. Nevertheless, we do not accept such a coincidence as true construction; we say that a construction produces the center if it produces it for any free choices.
- Solution
-
Arguing by contradiction, assume we have a verifying construction.
Apply an inversion in a circle perpendicular to \(\Gamma\) to the whole construction. According to Corollary 10.5.1, the circle \(\Gamma\) maps to itself. Since the inversion sends a circline to a circline, we get that the whole construction is mapped to an equivalent construction; that is, a constriction with a different choice of free points.
According to Exercise 10.3.1, the inversion sends the center of \(\Gamma\) to another point. However this construction claims that this another point is the center — a contradiction.
A similar example of impossible constructions for a ruler and a parallel tool is given in Exercise 14.2.4.
Let us discuss another example for a ruler-only construction. Note that ruler-only constructions are invariant with respect to the projective transformations. In particular, to solve the following exercise, it is sufficient to construct a projective transformation that fixes two points and moves their midpoint.
Show that there is no ruler-only construction verifying that a given point is a midpoint of a given segment. In particular it is impossible to construct the midpoint only with a ruler.
- Hint
-
Consider the perspective projection \((x,y) \mapsto (\tfrac{1}{x}, \tfrac{y}{x})\). Let \(A = (1, 1), B = (3, 1)\), and \(M = (2, 1)\). Note that \(M\) is the midpoint of \([AB]\).
Their images are \(A' = (1, 1)\), \(B' = (\tfrac{1}{3}, \tfrac{1}{3})\), and \(M' = (\tfrac{1}{2}, \tfrac{1}{2})\). Clearly, \(M'\) is note the midpoint of \([A'B']\).
The following theorem is a stronger version of the exercise above.
There is no ruler-only construction verifying that a given point is the center of a given circle. In particular it is impossible to construct the center only with a ruler.
The proof uses the construction in Theorem 16.3.2.
- Sketch of the proof
-
The same argument as in the problem above shows that it is sufficient to construct a projective transformation that sends the given circle \(\Gamma\) to a circle \(\Gamma'\) such that the center of \(\Gamma'\) is not the image of the center of \(\Gamma\).
Choose a circle \(\Gamma\) that lies in the plane \(\Pi\) in the Euclidean space. By Theorem 16.3.1, the inverse of a circle in a sphere is a circle or a line. Fix a sphere \(\Sigma\) with the center \(O\) so that the inversion \(\Gamma'\) of \(\Gamma\) is a circle and the plane \(\Pi'\) containing \(\Gamma'\) is not parallel to \(\Pi\); any sphere \(\Sigma\) in a general position will do.
Let \(Z\) and \(Z'\) denote the centers of \(\Gamma\) and \(\Gamma'\). Note that \(Z'\notin(OZ)\). It follows that the perspective projection \(\Pi\to \Pi'\) with center at \(O\) sends \(\Gamma\) to \(\Gamma'\), but \(Z'\) is not the image of \(Z\).


