2.7: The Hyp-Leg Theorem and Other Cases

Last updated
Save as PDF

Page ID: 34130

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

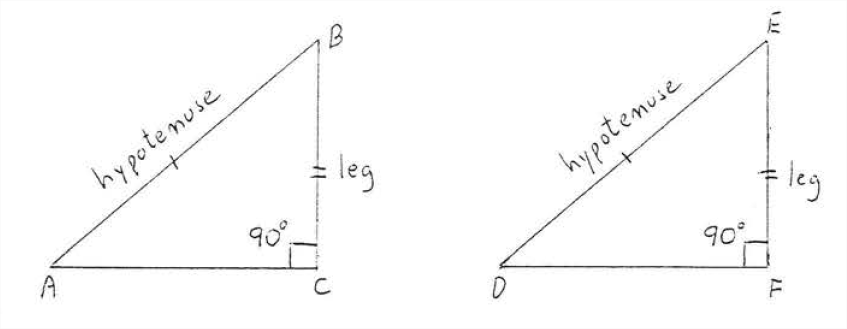
We give one more reason for two triangles to be congruent. Note that the following reason applies to right triangles only:

Theorem $\PageIndex{1}$: Hypotenuse-Leg Theorem

Two right triangles are congruent if the hypotenuse and a leg of one triangle are respectively equal to the hypotenuse and a leg of the other triangle (Hyp-Leg = Hyp-Leg)

In Figure $\PageIndex{1}$, if $AB = DE$ and $BC = BF$ then $\triangle ABC \cong \triangle DEF$.

Figure $\PageIndex{1}$: $\triangle ABC \cong \triangle DEF \text { because Hyp-Leg }=\text { Hyp-Leg.}$

Example $\PageIndex{1}$

Find $x$ and $y:$

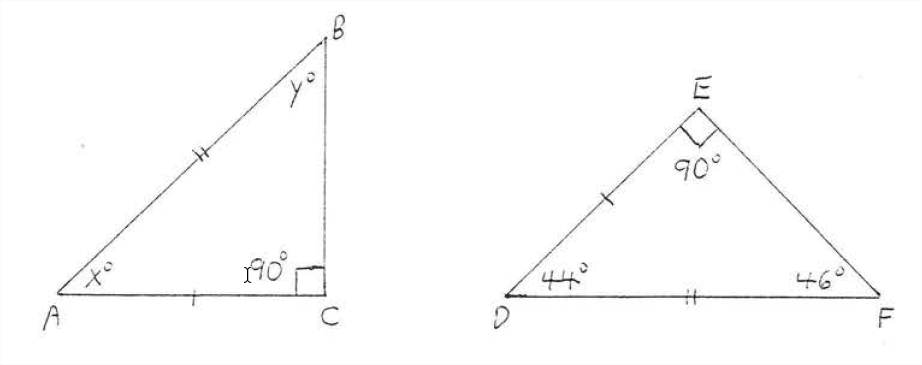
$clipboard_eb885ab57465b4ee7aa22d06c8f158bbd.png$

Solution

The hypotenuse of $\triangle ABC = AB =$ hypotenuse of $\triangle DBF = DF$ and a leg of $\triangle ABC = AC =$ a leg of $\triangle DEF = DE$. Therefore $\triangle ABC \cong \triangle DFE$ by Hyp-Leg = Hyp-Leg. So $x^{\circ} = \angle A = \angle D = 44^{\circ}$ and $y^{\circ} = \angle B = \angle F = 46^{\circ}$

Answer

$x=44, y=46$

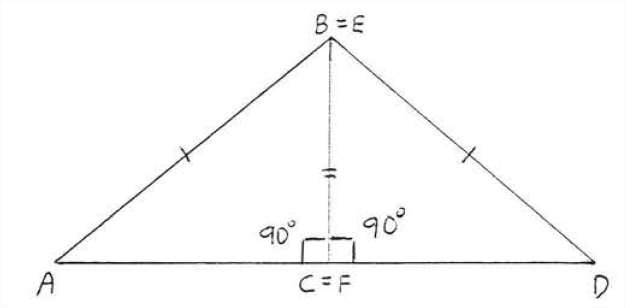
Proof of Theorem $\PageIndex{1}$: In Figure $\PageIndex{1}$, place $\triangle DEF$ so that $BC$ and $EF$ coincide (see Figure $\PageIndex{2}$). Then $\angle ACD = 180^{\circ}$ so $AD$ is a straight line segment. $\triangle ABD$ is isosceles with $AB = DE.$ Therefore $\angle A = \angle D$ because they are the base angles of isosceles triangle ABD (Theorem $\PageIndex{1}$, section 2.5). Then $\triangle ABC \cong \triangle DEF$ by $AAS = AAS$.

Figure $\PageIndex{2}$ Place $\triangle DEF$ so that $BC$ and $EF$ coincide.

Example $\PageIndex{2}$

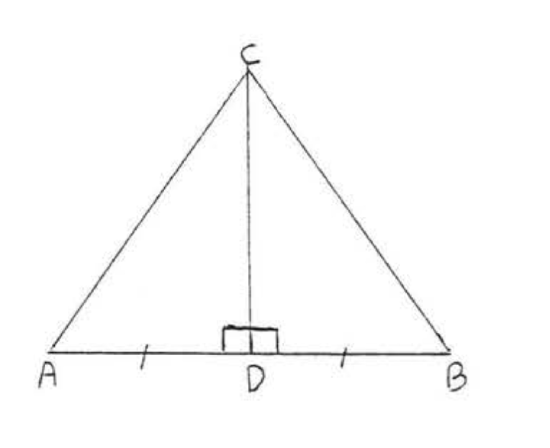
Given $AC = BC, CD \perp AB$. Prove $AD = BD$.

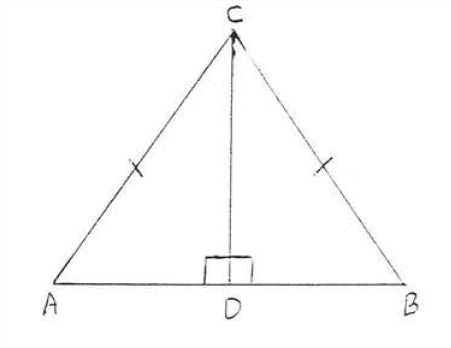
$clipboard_e42d08f1b63224e56ac14be804914699b.png$

Solution

Statements	Reasons
1. $AC = BC$.	1. Given.
2. $CD = CD$.	2. Identity.
3. $\angle ADC = \angle BDC = 90^{\circ}$.	3. Given $CD \perp AB$.
4. $\triangle ACD \cong \triangle BCD$.	4. Hyp-Leg = Hyp-Leg: Hyp $AC$, Leg $CD$ of $\triangle ACD =$ Hyp $BD$, Leg $CD$ of $\triangle BCD$.
5. $AD = BD$.	5. Corresponding sides of congruent triangles are equal.

At this point the student might be ready to conclude that two triangles are congruent whenever any three corresponding sides or angles are equal. However this is not true in the following two cases:

There may be two triangles that are not congruent but have two equal sides and an equal unincluded angle (SSA = SSA).

In Figure $\PageIndex{3}$, $AC = DF, BC = BF,$ and $\angle A = \angle D$ but none of the other angles or sides are equal.

Figure $\PageIndex{3}$: These two triangles satisfy $SSA = SSA$ but are not congruent.

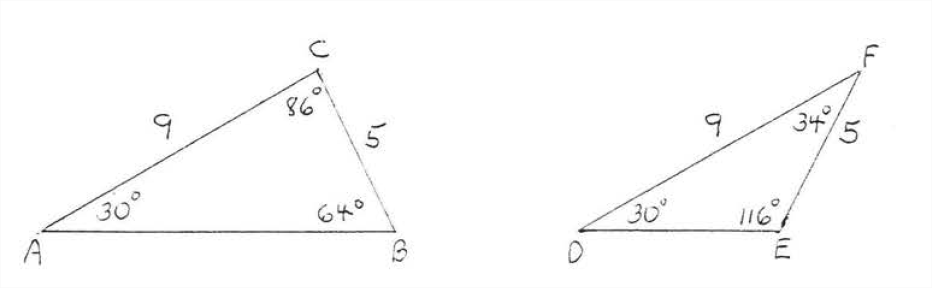
There are many triangles that are not congruent but have the same three angles $(AAA = AAA)$

In Figure $\PageIndex{4}$, the corresponding angles are equal but the corresponding sides are not.

Figure $\PageIndex{4}$. These triangles satisfy $AAA = AAA$ but are not congruent.

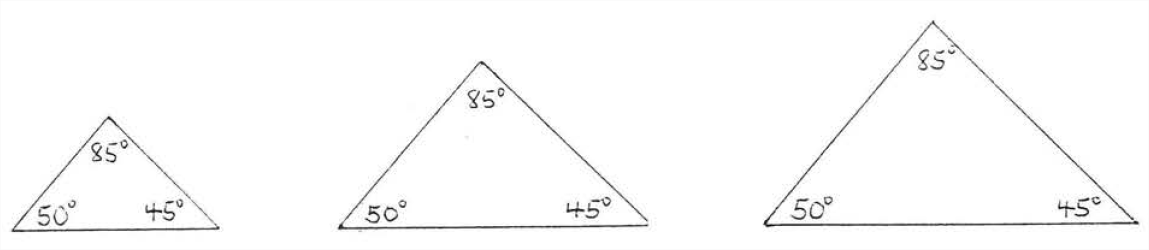
If $AAA = AAA$ the triangles are sald to be similar. Similar triangles are discussed in Chapter IV.

Example $\PageIndex{3}$

Determine if the triangles are congruent. If so write the congruence statement and find $x$.

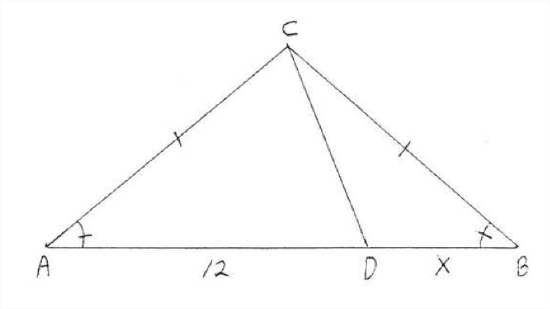
$clipboard_e9724b934e3714b755e209f6060a2b656.png$

Solution

Solution: From the diagram $AC = BC, CD = CD,$ and $\angle A = \angle B$ These are the only pairs of sides and angles which can be proven equal. $\angle A$ is not included between sides $AC$ and $CD$ and $\angle B$ is not included between sides $BC$ and $CD$. Therefore we have only $SSA = SSA$. We cannot conclude the triangles are congruent and we cannot find $x$.

Answer: The triangles cannot be proven congruent.

Summary

Valid Reasons for Congruence	Invalid Reasons for Congruence
$SAS = SAS$	$SSA = SSA$
$ASA = ASA$	$AAA = AAA$
$AAS = AAS$
$SSS = SSS$
Hyp-Leg = Hyp-Leg (right triangles only)

Problems

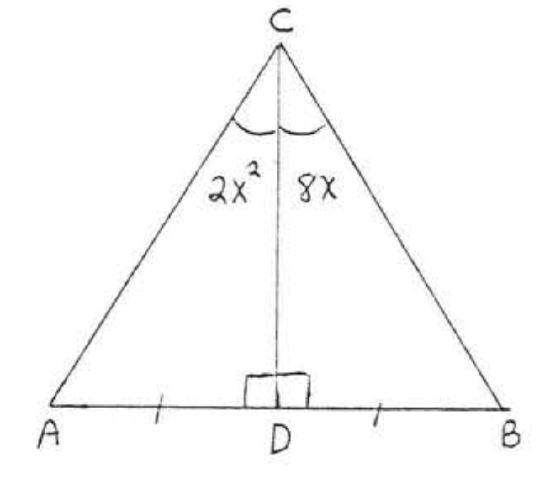
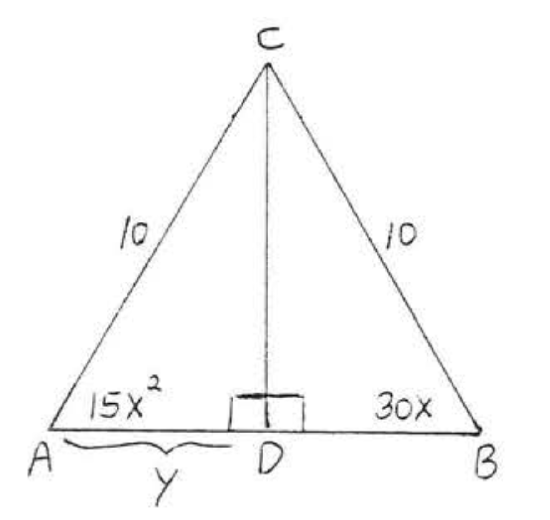
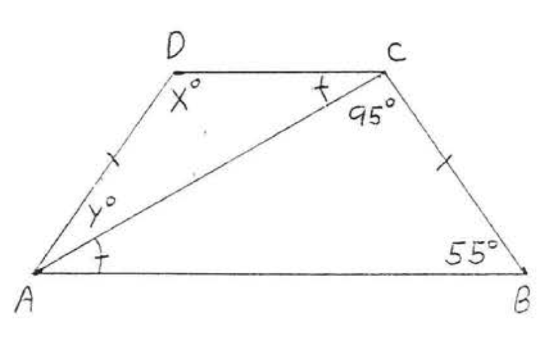
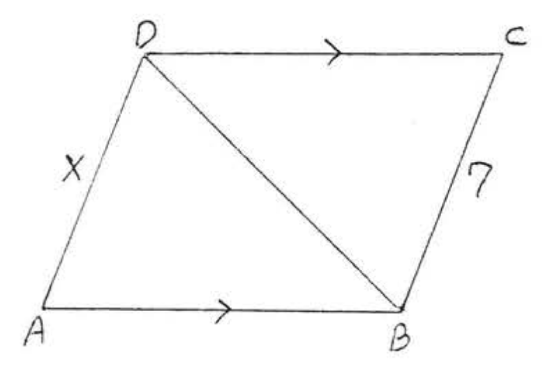
1 - 16. For each of the following determine if the triangles are congruent. If so

(1) write the congruence statement,

(2) give the reason for (1 ) ,

(3) find $x$, or $x$ and $y$, or $x$, $y$, and $z$,

Otherwise write "the triangles cannot be proven congruent."

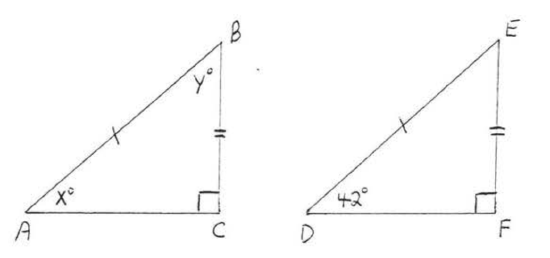
$Screen Shot 2020-11-02 at 6.04.19 PM.png$

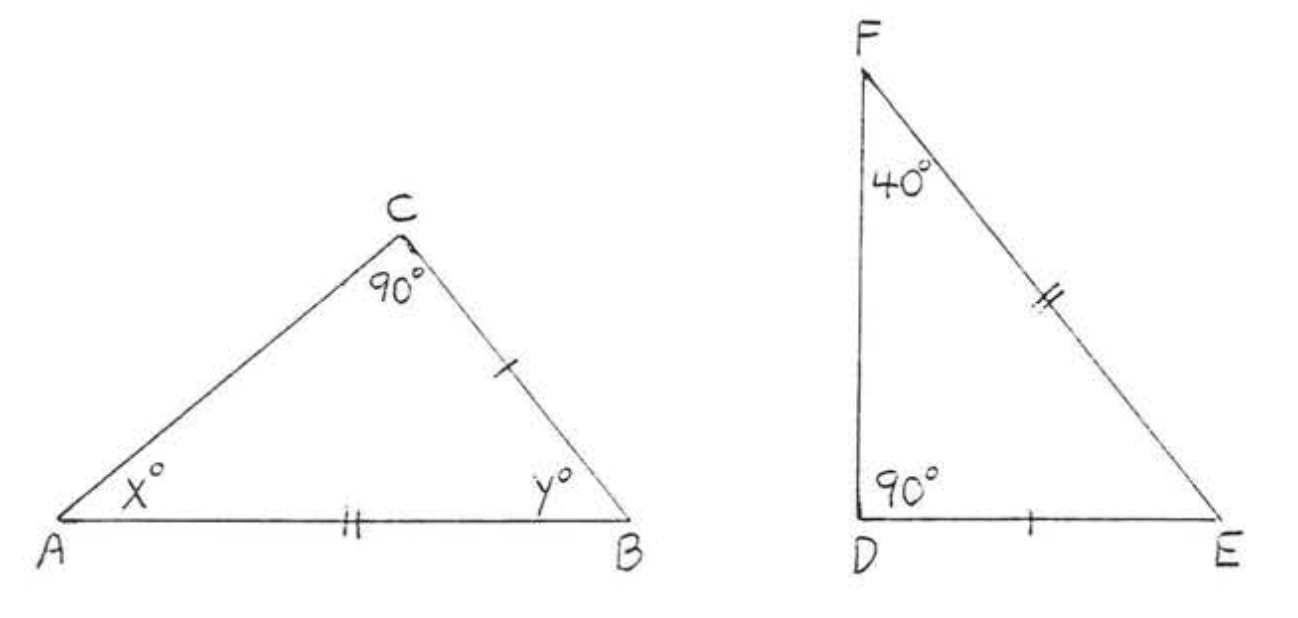
$Screen Shot 2020-11-02 at 6.04.37 PM.png$

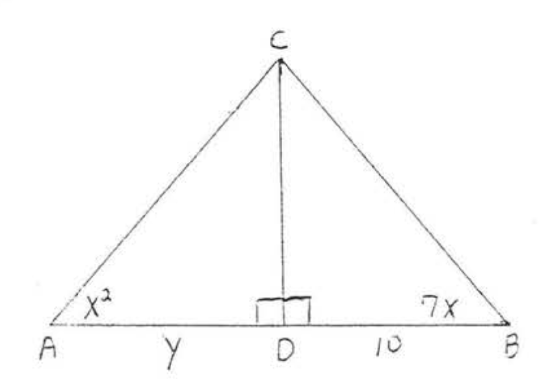
$Screen Shot 2020-11-02 at 6.04.55 PM.png$

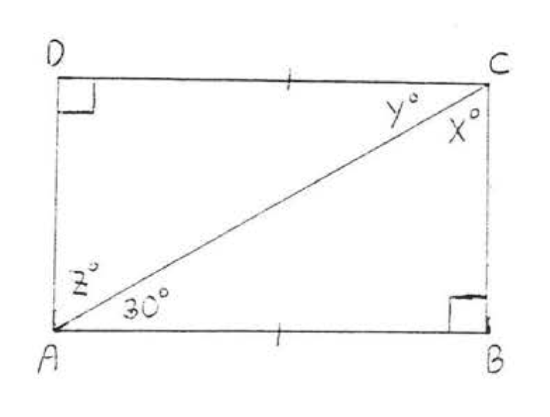
$Screen Shot 2020-11-02 at 6.05.13 PM.png$

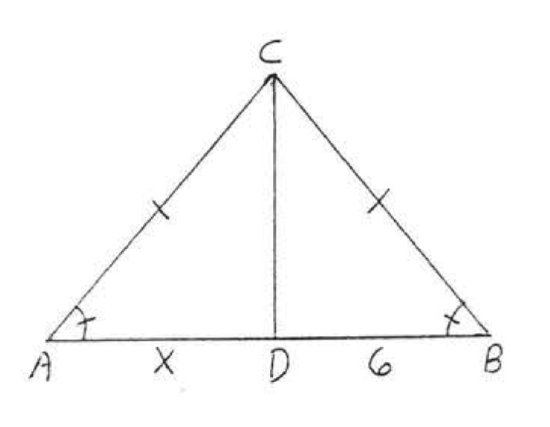
$Screen Shot 2020-11-02 at 6.05.34 PM.png$

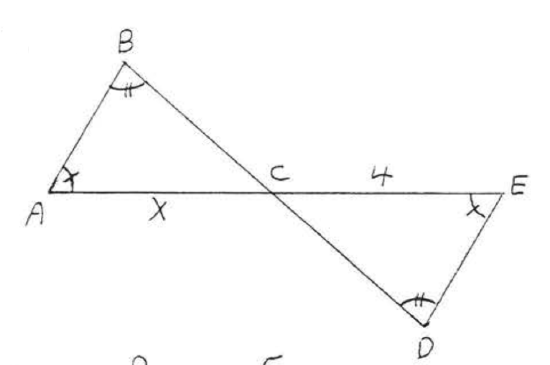
$Screen Shot 2020-11-02 at 6.06.34 PM.png$

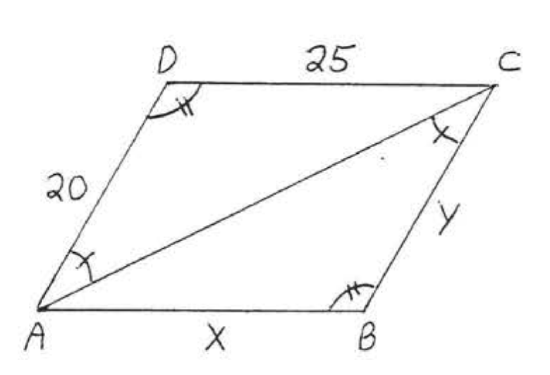
$Screen Shot 2020-11-02 at 6.06.50 PM.png$

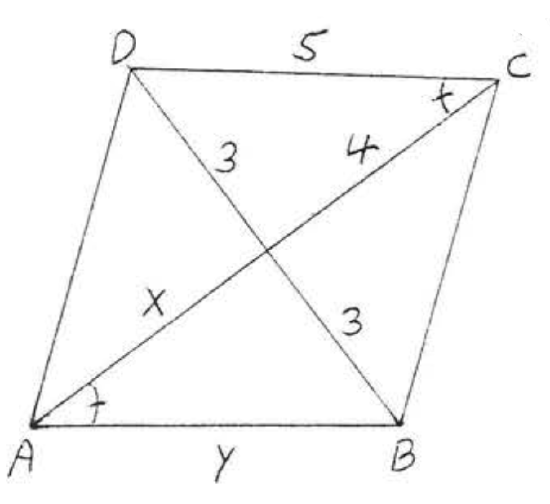
$Screen Shot 2020-11-02 at 6.12.09 PM.png$

$Screen Shot 2020-11-02 at 6.12.25 PM.png$

10.

$Screen Shot 2020-11-02 at 6.12.38 PM.png$

11.

$Screen Shot 2020-11-02 at 10.40.58 PM.png$

12.

$Screen Shot 2020-11-02 at 10.41.50 PM.png$

13.

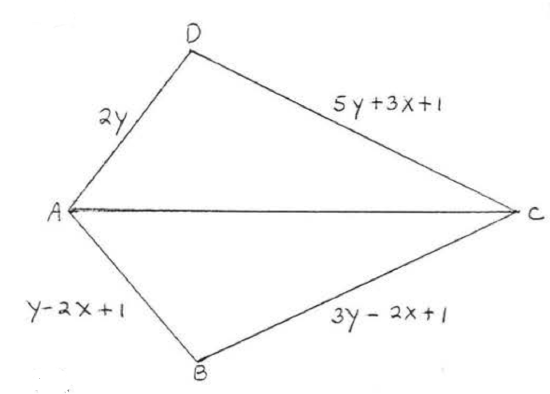
$Screen Shot 2020-11-02 at 10.42.27 PM.png$

14.

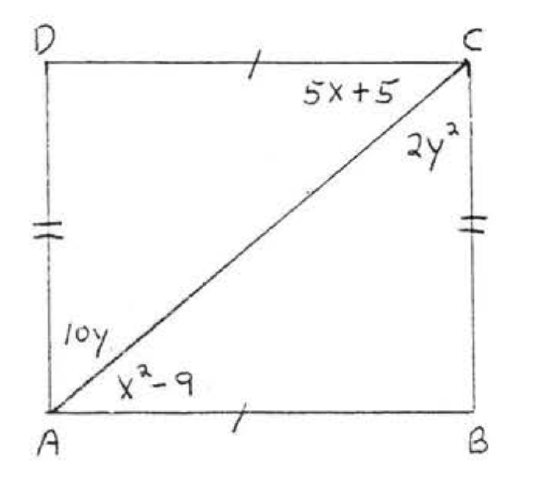
$Screen Shot 2020-11-02 at 10.42.42 PM.png$

15.

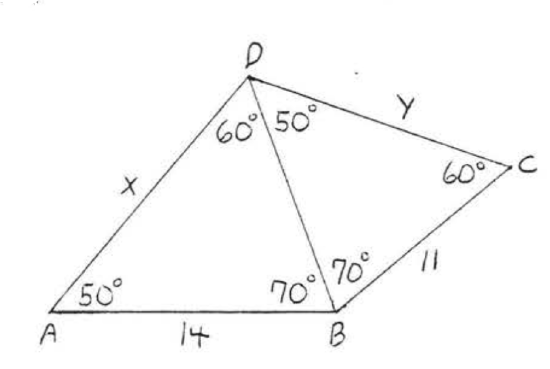
$Screen Shot 2020-11-02 at 10.43.02 PM.png$

16.

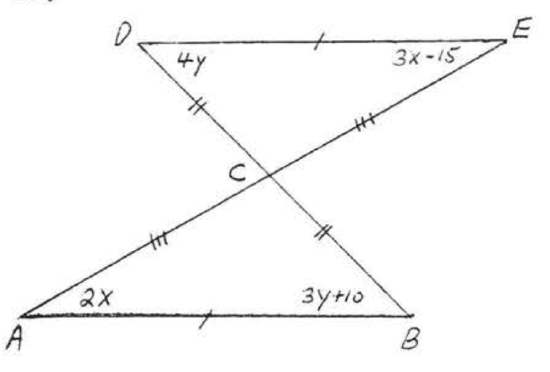
$Screen Shot 2020-11-02 at 10.43.36 PM.png$

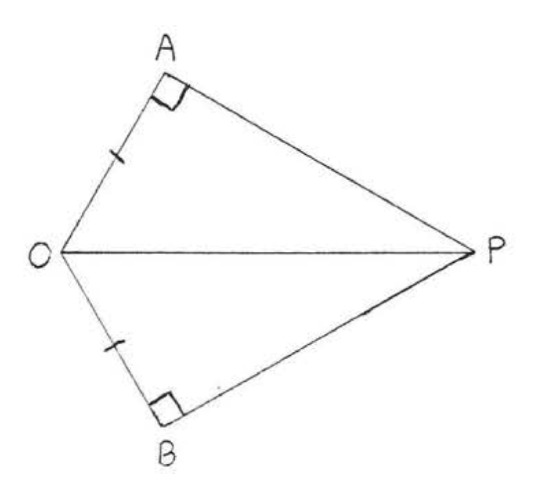
17. Given $CA = CB$ and $\angle A = \angle B = 90^{\circ}$. Prove $AP = BP$.

$Screen Shot 2020-11-02 at 10.44.00 PM.png$

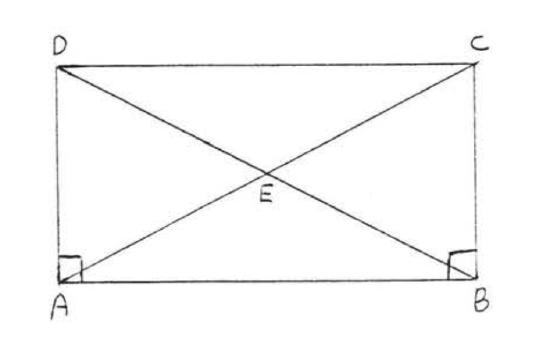
18. Given $AC = BD$ and $\angle A = \angle B = 90^{\circ}$. Prove $AD = BC$. (Hint: Show $\triangle ABC \cong \triangle BAD$)

$Screen Shot 2020-11-02 at 10.44.17 PM.png$

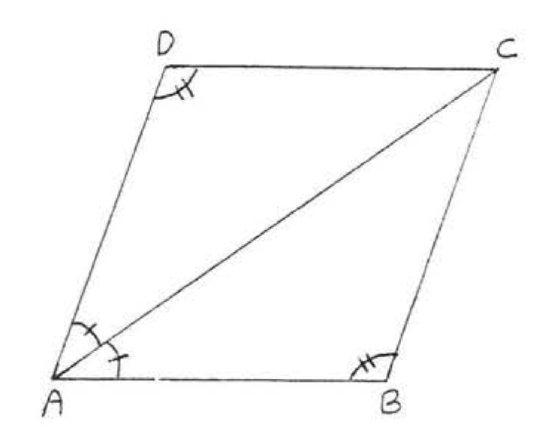
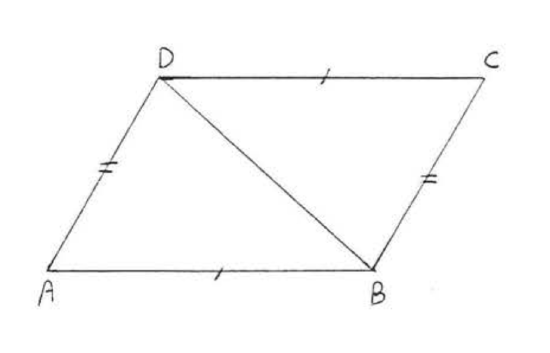
19. Given $AB = CD$ and $AD = CB$. Prove $\angle A = \angle C$.

$Screen Shot 2020-11-02 at 10.44.34 PM.png$

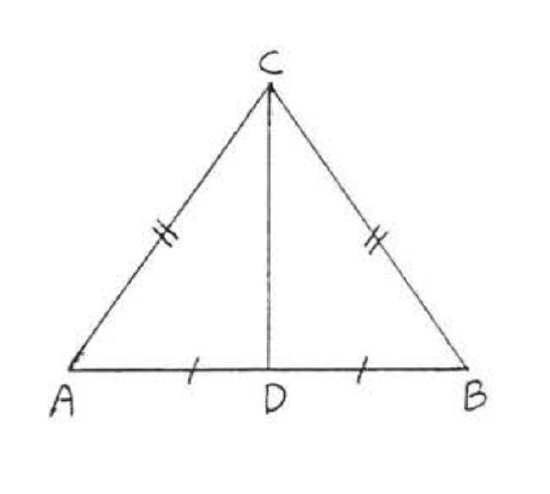
20. Given $AC = BC$ and $AD = BD$. Prove $\angle A = \angle B$.

$Screen Shot 2020-11-02 at 10.44.47 PM.png$

21. Given $AD = BD$ and $AB \perp CD$. Prove $\angle A = \angle B$.

$Screen Shot 2020-11-02 at 10.45.03 PM.png$

22. Given $\angle BAC = \angle DAC$ and $\angle B = \angle D$. Prove $AB = AD$.

$Screen Shot 2020-11-02 at 10.45.15 PM.png$

Statements	Reasons
1. \(AC = BC\).	1. Given.
2. \(CD = CD\).	2. Identity.
3. \(\angle ADC = \angle BDC = 90^{\circ}\).	3. Given \(CD \perp AB\).
4. \(\triangle ACD \cong \triangle BCD\).	4. Hyp-Leg = Hyp-Leg: Hyp \(AC\), Leg \(CD\) of \(\triangle ACD =\) Hyp \(BD\), Leg \(CD\) of \(\triangle BCD\).
5. \(AD = BD\).	5. Corresponding sides of congruent triangles are equal.

Valid Reasons for Congruence	Invalid Reasons for Congruence
\(SAS = SAS\)	\(SSA = SSA\)
\(ASA = ASA\)	\(AAA = AAA\)
\(AAS = AAS\)
\(SSS = SSS\)
Hyp-Leg = Hyp-Leg (right triangles only)

Theorem \(\PageIndex{1}\): Hypotenuse-Leg Theorem

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Summary