4.5: On side-side-angle and side-angle-angle
- Page ID
- 23602
In each of the conditions SAS, ASA, and SSS we specify three corresponding parts of the triangles. Let us discuss other triples of corresponding parts.
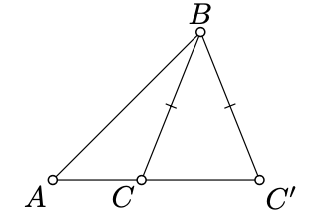
The fist triple is called side-side-angle, or briefly SSA; it specifies two sides and a non-included angle. This condition is not sufficient for congruence; that is, there are two nondegenerate triangles \(ABC\) and \(A'B'C'\) such that
\(AB = A'B',\) \(BC = B'C'\), \(\measuredangle BAC \equiv \pm \measuredangle B'A'C'\),
but \(\triangle ABC \not\cong \triangle A'B'C'\) and moreover \(AC \ne A'C'\).
We will not use this negative statement in the sequel and therefore there is no need to prove it formally. An example can be guessed from the diagram.
The second triple is side-angle-angle, or briefly SAA; it specifies one side and two angles one of which is opposite to the side. This provides a congruence condition; that is, if one of the triangles \(ABC\) or \(A'B'C'\) is nondegenerate and \(AB = A'B'\), \(\measuredangle ABC \equiv \pm \measuredangle A'B'C'\), \(\measuredangle BCA \equiv \pm \measuredangle B'C'A'\), then \(\triangle ABC \cong \triangle A'B'C'\).
The SAA condition will not be used directly in the sequel. One proof of this condition can be obtained from ASA and the theorem on the sum of angles of a triangle proved below (see Theorem 7.4.1). For a more direct proof, see Exercise 11.1.2.
Another triple is called angle-angle-angle, or briefly AAA; by Axiom V, it is not a congruence condition in the Euclidean plane, but in the hyper-bolic plane it is; see Theorem 13.3.2.


