8.3: Medians and centroid

Last updated
Save as PDF

Page ID: 23628

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A median of a triangle is the segment joining a vertex to the midpoint of the opposing side.

Theorem $\PageIndex{1}$

The three medians of any nondegenerate triangle intersect in a single point. Moreover, the point of intersection divides each median in the ratio 2:1.

The point of intersection of medians is called the centroid of the tri- angle; it is usually denoted by M. In the proof we will apply Exercise 3.4.3 and Exercise7.3.1; their complete solutions are given in the hits.

Proof

Consider a nondegenerate triangle $ABC$. Let $[AA']$ and $[BB']$ be its medians. According to Exercise 3.4.3, $[AA']$ and $[BB']$ have a point of intersection; denote it by $M$.

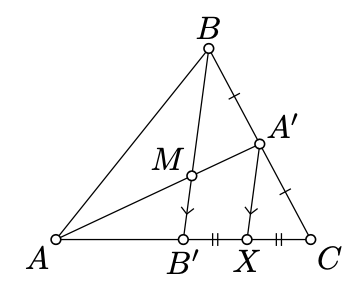
$截屏2021-02-15 下午3.30.48.png$

Draw a line $\ell$ thru $A'$ parallel to $(BB')$. Applying Exercise7.3.1 for $\triangle BB'C$ and $\ell$, we get that $\ell$ cross $[B'C]$ at some point $X$ and

$\dfrac{CX}{CB'} = \dfrac{CA'}{CB} = \dfrac{1}{2};$

that is, $X$ is the midpoint of $[CB']$.

Since $B'$ is the midpoint of $[AC]$ and $X$ is the midpoint of $[B'C]$, we get that

$\dfrac{AB'}{AX} = \dfrac{2}{3}.$

Applying Exercise 7.3.1 for $\triangle XA'A$ and the line $(BB')$, we get that

\[\dfrac{AM}{AA'} = \dfrac{AB'}{AX} = \dfrac{2}{3};\]

that is, $M$ divides $[AA']$ in the ratio 2:1.

Note that 8.3.1 uniquely defines $M$ on $[AA']$. Repeating the same argument for medians $[AA']$ and $[CC']$, we get that they intersect at $M$ as well, hence the result.

Exercise $\PageIndex{1}$

Let $\square ABCD$ be a nondegenerate quadrangle and $X, Y, V, W$ be the midpoints of its sides $[AB], [BC], [CD]$, and $[DA]$. Show that $\square XYVW$ is a parallelogram.

Hint: Use the idea from the proof of Theorem $\PageIndex{1}$ to show that $(XY) \parallel (AC) \parallel (VW)$ and $(XV) \parallel (BD) \parallel (YW)$.