5.3: The Inverse Laplace Transform

Last updated
Save as PDF

Page ID: 21828

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

To Come

In The transfer Function we shall establish that the inverse Laplace transform of a function \(h\) is

\[\mathscr{L}^{-1}(h)(t) = \frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{(c+yi)t} h((c+yi)t) dy \nonumber\]

where \(i \equiv \sqrt{2-1}\) and the real number \(c\) is chosen so that all of the singularities of \(h\) lie to the left of the line of integration.

Proceeding with the Inverse Laplace Transform

With the inverse Laplace transform one may express the solution of \(\textbf{x}' = B\textbf{x}+\textbf{g}\), as

\[x(t) = \mathscr{L}^{-1} ((sI-B)^{-1}) (\mathscr{L}(\textbf{g}+x(0)) \nonumber\]

As an example, let us take the first component of \(\mathscr{L}(x)\), namely

\[\mathscr{L}_{x_{1}} (s) = \frac{0.19(s^2+1.5s+0.27)}{(s+\frac{1}{6})^{4}(s^3+1.655s^2+0.4078s+0.0039)} \nonumber\]

We define:

Definition: Pole

Also called singularities, these are the points ss at which \(\mathscr{L}_{x_{1}}⁢(s)\) blows up.

These are clearly the roots of its denominator, namely

\[\begin{array}{cccc} {-1/100}&{-329/400 \pm \frac{\sqrt{273}}{16}}&{and}&{-1/6} \end{array} \nonumber\]

All four being negative, it suffices to take \(c = 0\) and so the integration in Equation proceeds up the imaginary axis. We don't suppose the reader to have already encountered integration in the complex plane but hope that this example might provide the motivation necessary for a brief overview of such. Before that however we note that MATLAB has digested the calculus we wish to develop. Referring again to fib3.m for details we note that the ilaplace command produces

\[x_{1}(t) = 211.35e^{\frac{-t}{100}}-(0.0554t^3+4.5464t^2+1.085t+474.19)e^{\frac{-t}{6}}+e^{\frac{-(329t)}{400}}(262.842 \cosh (\frac{\sqrt{273}t}{16})) +262.836 \sinh (\frac{\sqrt{273}t}{16})) \nonumber\]

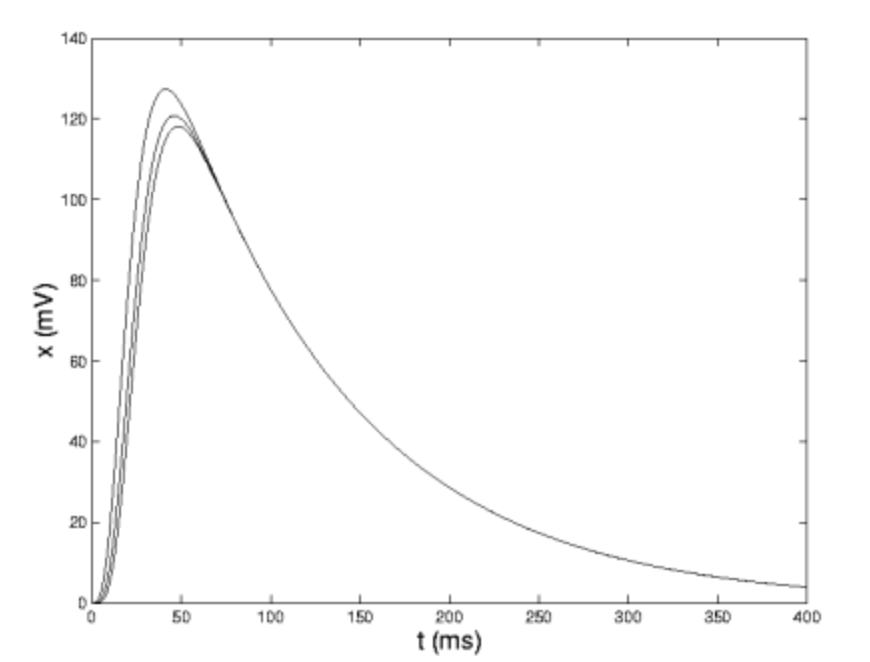
Screen Shot 2020-10-04 at 4.27.22 PM.png — Figure 1. The 3 potentials associated with the RC circuit model figure.

The other potentials, see the figure above, possess similar expressions. Please note that each of the poles of \(\mathscr{L}(⁢x_{1})\) appear as exponents in \(x_{1}\) and that the coefficients of the exponentials are polynomials whose degrees is determined by the order of the respective pole.