9.6: Orthogonal projections and minimization problems
- Page ID
- 261
Definition 9.6.1 Let \(V \) be a finite-dimensional inner product space and \(U\subset V \) be a subset (but not necessarily a subspace) of \(V\). Then the orthogonal complement of \(U \) is defined to be the set
\[ U^\bot = \{ v \in V \mid \inner{u}{v}=0 ~\rm{for~ all}~ u\in U \} .\]
Note that, in fact, \(U^\bot \) is always a subspace of \(V \) (as you should check!) and that
\[ \{0\}^\bot = V \quad \text{and} \quad V^\bot = \{0\}. \]
In addition, if \(U_{1} \) and \(U_{2} \) are subsets of \(V \) satisfying \(U_1\subset U_2\), then \(U_2^\bot \subset U_1^\bot\). Remarkably, if \(U\subset V \) is a subspace of \(V\), then we can say quite a bit more about \(U^{\bot}\).
Theorem 9.6.2. If \(U\subset V \) is a subspace of \(V\), then \(V=U\oplus U^\bot\).
Proof. We need to show two things:
- \(V=U+U^\bot\).
- \(U\cap U^\bot = \{0\}\).
To show Condition~1 holds, let \((e_1,\ldots,e_m) \) be an orthonormal basis of \(U\). Then, for all \(v\in V\), we can write
\begin{equation} \label{eq:U Ubot}
v=\underbrace{\inner{v}{e_1} e_1 + \cdots + \inner{v}{e_m} e_m}_u +
\underbrace{v-\inner{v}{e_1} e_1 - \cdots - \inner{v}{e_m} e_m}_w. \tag{9.6.1}
\end{equation}
The vector \(u\in U\), and
\begin{equation*}
\inner{w}{e_j} = \inner{v}{e_j} - \inner{v}{e_j} =0, ~\rm{for~ all}~ {j=1,2,\ldots,m , }
\end{equation*}
since \((e_1,\ldots,e_m) \) is an orthonormal list of vectors. Hence, \(w\in U^\bot\). This implies that \(V=U+U^\bot\).
To prove that Condition~2 also holds, let \(v\in U\cap U^\bot\). Then \(v \) has to be orthogonal to every vector in \(U\), including to itself, and so \(\inner{v}{v}=0\). However, this implies \(v=0 \) so that \(U\cap U^\bot=\{0\}\).
Example 9.6.3. \(\mathbb{R}^2 \) is the direct sum of any two orthogonal lines, and \(\mathbb{R}^3 \) is the direct sum of any plane and any line orthogonal to the plane as illustrated in Figure 9.6.1. For example,
\begin{equation*}
\begin{split}
\mathbb{R}^2 &= \{(x,0) \mid x\in \mathbb{R}\} \oplus \{ (0,y) \mid y\in\mathbb{R}\},\\
\mathbb{R}^3 &= \{(x,y,0) \mid x,y\in \mathbb{R}\} \oplus \{(0,0,z) \mid z\in \mathbb{R}\}.
\end{split}
\end{equation*}
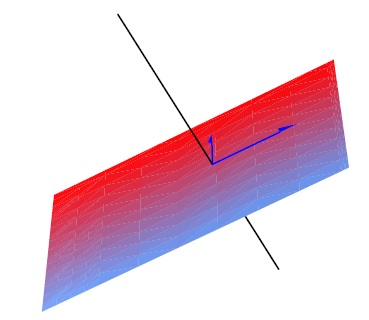
Figure 9.6.1: \( \mathbb{R^3} \) as a direct sum of a plane and a line.
Another fundamental fact about the orthogonal complement of a subspace is as follows.
Theorem 9.6.4. If \(U\subset V \) is a subspace of \(V\), then \(U=(U^\bot)^\bot\).
Proof. First we show that \(U\subset (U^\bot)^\bot\). Let \(u\in U\). Then, for all \(v\in U^\bot\), we have \(\inner{u}{v}=0\). Hence, \(u\in (U^\bot)^\bot \) by the definition of \((U^\bot)^\bot\).
Next we show that \((U^\bot)^\bot\subset U\). Suppose \(0\neq v\in (U^\bot)^\bot \) such that \(v\not\in U\), and decompose \(v \) according to Theorem 9.6.2, i.e., as
\begin{equation*}
v = u_1 + u_2 \in U \oplus U^\bot
\end{equation*}
with \(u_1\in U \) and \(u_2\in U^\bot\). Then \(u_2\neq 0 \) since \(v\not\in U\).
Furthermore, \(\inner{u_2}{v} = \inner{u_2}{u_2} \neq 0\). But then \(v \) is not in \((U^\bot)^\bot\), which contradicts our initial assumption. Hence, we must have that \((U^\bot)^\bot\subset U\).
By Theorem 9.6.2, we have the decomposition \(V=U\oplus U^\bot \) for every subspace \(U\subset V\). This allows us to define the orthogonal projection \(P_U \) of \(V \) onto \(U\).
Definition 9.6.5. Let \(U\subset V \) be a subspace of a finite-dimensional inner product space. Every \(v\in V \) can be uniquely written as \(v=u+w \) where \(u\in U \) and \(w\in U^\bot\). Define
\begin{equation*}
\begin{split}
P_U:V &\to V,\\
v &\mapsto u.
\end{split}
\end{equation*}
Note that \(P_U \) is called a projection operator since it satisfies \(P_U^2=P_U\). Further, since we also have
\begin{equation*}
\begin{split}
&\range(P_U)= U,\\
&\kernel(P_U) = U^\bot,
\end{split}
\end{equation*}
it follows that \(\range(P_U) \bot \kernel(P_U)\). Therefore, \(P_U \) is called an orthogonal projection.
The decomposition of a vector \(v\in V\) as given in Equation (9.6.1) yields the formula
\begin{equation} \label{eq:ortho decomp}
P_U v = \inner{v}{e_1} e_1 + \cdots + \inner{v}{e_m} e_m, \tag{9.6.2}
\end{equation}
where \((e_1,\ldots,e_m) \) is any orthonormal basis of \(U\). Equation (9.6.2) is a particularly useful tool for computing such things as the matrix of \(P_{U} \) with respect to the basis \((e_1,\ldots,e_m)\).
Let us now apply the inner product to the following minimization problem: Given a subspace \(U\subset V \) and a vector \(v\in V\), find the vector \(u\in U \) that is closest to the vector \(v\). In other words, we want to make \(\norm{v-u} \) as small as possible. The next proposition shows that \(P_Uv \) is the closest point in \(U \) to the vector \(v \) and that this minimum is, in fact, unique.
Proposition 9.6.6. Let \(U\subset V \) be a subspace of \(V \) and \(v\in V\). Then
\[ \norm{v-P_Uv} \le \norm{v-u} \qquad \text{for every \(u\in U\).}\]
Furthermore, equality holds if and only if \(u=P_Uv\).
Proof. Let \(u\in U \) and set \(P:=P_U \) for short. Then
\begin{equation*}
\begin{split}
\norm{v-P v}^2 &\le \norm{v-P v}^2 + \norm{Pv-u}^2\\
&= \norm{(v-P v)+(P v-u)}^2 = \norm{v-u}^2,
\end{split}
\end{equation*}
where the second line follows from the Pythagorean Theorem 9.3.2~\ref{thm:pythagoras} since \(v-Pv\in U^\bot \) and \(Pv-u\in U\). Furthermore, equality holds only if \(\norm{Pv-u}^2=0\), which is equivalent to \(Pv=u\).
Example 9.6.7. Consider the plane \(U\subset \mathbb{R}^3 \) through 0 and perpendicular to the vector \(u=(1,1,1)\). Using the standard norm on \(\mathbb{R}^3\), we can calculate the distance of the point \(v=(1,2,3) \) to \(U \) using Proposition 9.6.6. In particular, the distance \(d \) between \(v \) and \(U \) is given by \(d=\norm{v-P_Uv}\). Let \((\frac{1}{\sqrt{3}}u,u_1,u_2) \) be a basis for \(\mathbb{R}^3 \) such that \((u_1,u_2) \) is an orthonormal basis of \(U\). Then, by Equation (9.6.2), we have
\begin{align*}
v-P_Uv & = (\frac{1}{3}\inner{v}{u}u+\inner{v}{u_1}u_1+\inner{v}{u_2}u_2) - (\inner{v}{u_1}u_1 +\inner{v}{u_2}u_2)\\
& = \frac{1}{3}\inner{v}{u}u\\
& = \frac{1}{3}\inner{(1,2,3)}{(1,1,1)}(1,1,1)\\
& = (2,2,2).
\end{align*}
Hence, \(d=\norm{(2,2,2)}=2\sqrt{3}\).
Contributors
- Isaiah Lankham, Mathematics Department at UC Davis
- Bruno Nachtergaele, Mathematics Department at UC Davis
- Anne Schilling, Mathematics Department at UC Davis
Both hardbound and softbound versions of this textbook are available online at WorldScientific.com.


