7.2: Cauchy's Integral Formula
- Page ID
- 21841
The Residue Theorem
After Cauchy's Theorem perhaps the most useful consequence of Cauchy's Theorem is the The Curve Replacement Lemma
Suppose that \(C_{2}\) is a closed curve that lies inside the region encircled by the closed curve \(C_{1}\). If \(f\) is differentiable in the annular region outside \(C_{2}\) and inside \(C_{1}\) then
\[\int f(z) dz = \int f(z) dz \nonumber\]
With reference to Figure 1, we introduce two vertical segments and define the closed curves \(C_{3} = abcda\) (where the \(bc\) arc is clockwise and the \(da\) arc is counterclockwise) and \(C_{4} = adcba\) (where the \(ad\) arc is counter-clockwise and the \(cb\) arc is clockwise). By merely following the arrows we learn that
\[\int f(z)dz = \int f(z)dz+\int f(z)dz+\int f(z)dz \nonumber\]
As Cauchy's Theorem implies that the integrals over \(C_{3}\) and \(C_{4}\) each vanish, we have our result.
Curve Replacement Figure
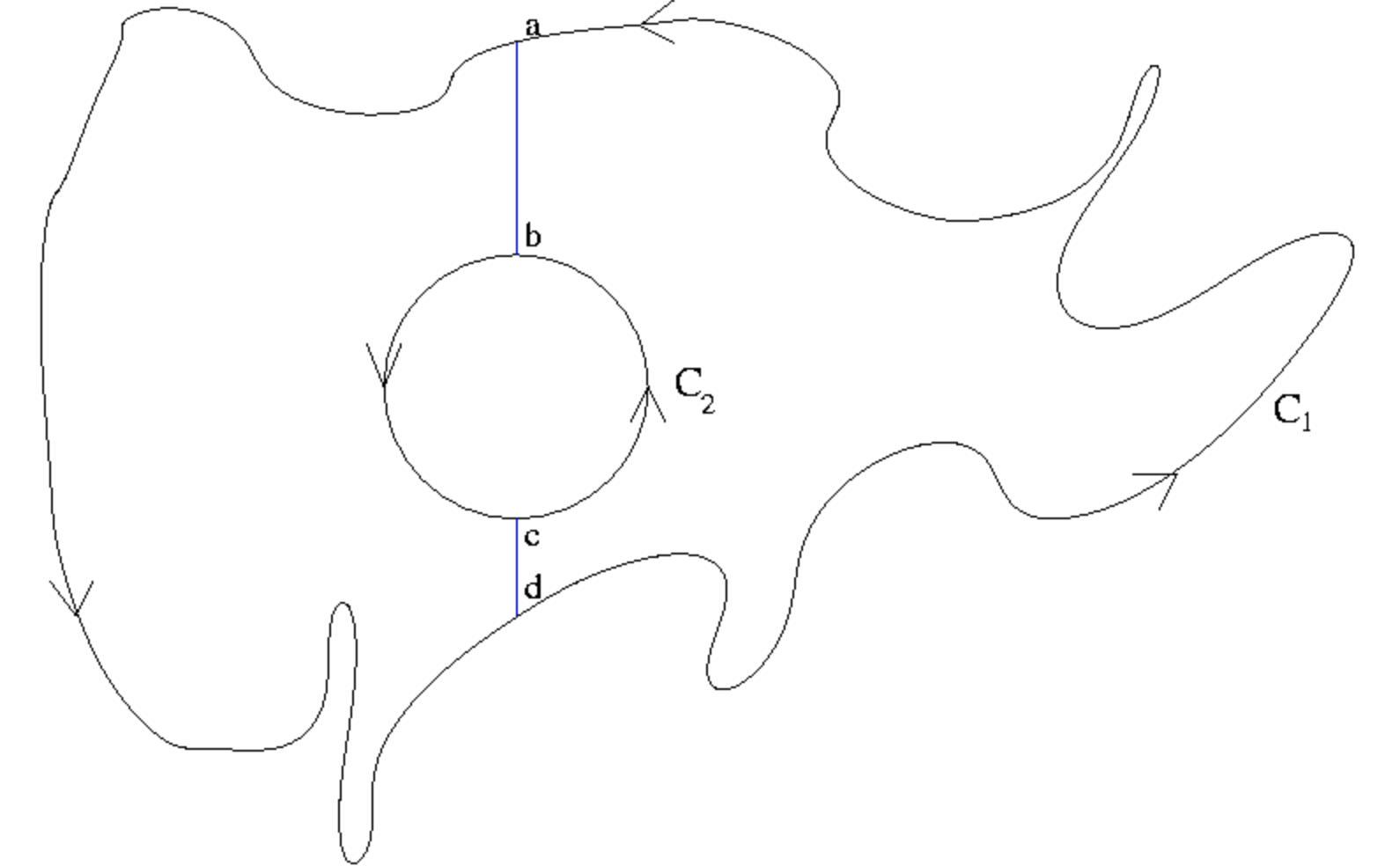
This Lemma says that in order to integrate a function it suffices to integrate it over regions where it is singular, i.e. nondifferentiable.
Let us apply this reasoning to the integral
\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz \nonumber\]
where \(C\) encircles both \(\lambda_{1}\) and \(\lambda_{2}\) as depicted in Figure. We find that
\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz = \int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz+\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz \nonumber\]
Developing the integrand in partial fractions we find
\[\begin{align*} \int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz &= \int \frac{\lambda_{1}}{\lambda_{1}-\lambda_{2}}\int \frac{1}{(z-\lambda_{1})} dz+\int \frac{\lambda_{2}}{\lambda_{2}-\lambda_{1}}\int \frac{1}{(z-\lambda_{2})} dz \\[4pt] &= \frac{2\pi i \lambda_{1}}{\lambda_{1}-\lambda_{2}} \end{align*}\]
Similarly,
\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz = \frac{2\pi i \lambda_{1}}{\lambda_{1}-\lambda_{2}} \nonumber\]
Putting things back together we find
\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz = 2\pi i \left(\frac{\lambda_{1}}{\lambda_{1}-\lambda_{2}}-\frac{\lambda_{2}}{\lambda_{2}-\lambda_{1}} \right) \nonumber\]
\[= 2 \pi i \nonumber\]
Figure 2. Concentrating on the poles.
We may view Equation as a special instance of integrating a rational function around a curve that encircles all of the zeros of its denominator. In particular, recalling that Cauchy's Theorem, we find
\[\int q(z) dz = \sum_{j = 1}^{h} \sum_{k = 1}^{m_{j}} \int \frac{q_{j,k}}{(z-\lambda_{j})^k} dz = 2\pi i \sum_{j = 1}^{h} q_{j,1} \nonumber\]
To take a slightly more complicated example let us integrate \(\frac{f(z)}{z-a}\) over some closed curve \(C\) inside of which \(f\) is differentiable and \(a\) resides. Our Curve Replacement Lemma now permits us to claim that
\[\int \frac{f(z)}{z-a} dz = \int \frac{f(z)}{z-a} dz \nonumber\]
It appears that one can go no further without specifying \(f\). The alert reader however recognizes that in the integral over \(C(a,r)\) is independent of rr and so proceeds to let \(r \rightarrow 0\), in which case \(z \rightarrow a\) and \(f(z) \rightarrow f(a)\). Computing the integral of \(\frac{1}{z-a}\) along the way we are led to the hope that
\[\int \frac{f(z)}{z-a} dz = f(a) 2 \pi i \nonumber\]
In support of this conclusion we note that
\[\int \frac{f(z)}{z-a} dz = \int \frac{f(z)}{z-a} dz+\int \frac{f(a)}{z-a} dz-\int \frac{f(a)}{z-a} dz f(a) = f(a) \int \frac{1}{z-a} dz+\int \frac{f(z)-f(a)}{z-a} dz \nonumber\]
Now the first term is \(f(a) 2\pi i\) regardless of \(r\) while, as \(r \rightarrow 0\) the integrand of the second term approaches \(\frac{d}{da}f(a)\) and the region of integration approaches the point \(a\). Regarding this second term, as the integrand remains bounded as the perimeter of \(C(a,r)\) approaches zero the value of the integral must itself be zero. This result if typically known as
If \(f\) is differentiable on and in the closed curve \(C\) then
\[f(a) = \frac{1}{2\pi i} \int \frac{f(z)}{z-a} dz \nonumber\]
for each a lying inside \(C\).
The consequences of such a formula run far and deep. We shall delve into only one or two. First, we note that, as a does not lie on \(C\), the right hand side is a perfectly smooth function of \(a\). Hence, differentiating each side, we find
\[\frac{d}{da} f(a) = \frac{1}{2\pi i} \int \frac{f(z)}{(z-a)^2} dz \nonumber\]
for each a lying inside \(C\). Applying this reasoning nn times we arrive at a formula for the n-th derivative of \(f\) at \(a\)
\[\frac{d^n}{da^n} f(a) = \frac{n!}{2\pi i} \int \frac{f(z)}{(z-a)^{1+n}} dz \nonumber\]
for each a lying inside \(C\). The upshot is that once \(f\) is shown to be differentiable it must in fact be infinitely differentiable. As a simple extension let us consider
\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz \nonumber\]
where \(f\) is still assumed differentiable on and in \(C\) and that \(C\) encircles both \(\lambda_{1}\) and \(\lambda_{2}\). By the curve replacement lemma this integral is the sum
\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz+\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} \nonumber\]
where \(\lambda_{j}\) now lies in only \(C_{j}\). As \(\frac{f(z)}{z-\lambda_{2}}\) is well behaved in \(C_{1}\) we may use Equation to conclude that
\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz = \frac{f(\lambda_{1})}{(\lambda_{1}-\lambda_{2})^2} \nonumber\]
Similarly, as \(\frac{f(z)}{z-\lambda_{1}}\) is well behaved in \(C_{2}\) we may use Equation to conclude that
\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz = \frac{d}{da} (\frac{f(a)}{a-\lambda_{1}}) |_{a=\lambda_{2}} \nonumber\]
These calculations can be read as a concrete instance of
If \(g\) is a polynomial with roots \(\{\lambda_{j} | j = \{1, \cdots, h\}\}\) of degree \(\{d_{j} | j = \{1, \cdots, h\}\}\) and \(C\) is a closed curve encircling each of the \(\lambda_{j}\) and \(f\) is differentiable on and in \(C\) then
\[\int \frac{f(z)}{g(z)} dz = 2 \pi i \sum_{j = 1}^{h} res(\lambda_{j}) \nonumber\]
where
\[res(\lambda_{j}) = lim_{z\rightarrow \lambda_{j}} \frac{1}{(d_{j}-1)!} \frac{d^{d_{j}-1} (z-\lambda_{j})^{d_{j}} \frac{f(z)}{g(z)}}{dz^{d_{j}-1}} \nonumber\]
is called the residue of \(\frac{f}{g}\) at \(\lambda_{j}\).
One of the most important instances of this theorem is the formula for the Inverse Laplace Transform.


