4.3: Determinants and Volumes

Last updated
Save as PDF

Page ID: 70204

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectives

Understand the relationship between the determinant of a matrix and the volume of a parallelepiped.
Learn to use determinants to compute volumes of parallelograms and triangles.
Learn to use determinants to compute the volume of some curvy shapes like ellipses.
Pictures: parallelepiped, the image of a curvy shape under a linear transformation.
Theorem: determinants and volumes.
Vocabulary word: parallelepiped.

In this section we give a geometric interpretation of determinants, in terms of volumes. This will shed light on the reason behind three of the four defining properties of the determinant, Definition 4.1.1 in Section 4.1. It is also a crucial ingredient in the change-of-variables formula in multivariable calculus.

Parallelograms and Paralellepipeds

The determinant computes the volume of the following kind of geometric object.

Definition $\PageIndex{1}$: Paralellepiped

The paralellepiped determined by $n$ vectors $v_1, v_2,\ldots,v_n$ in $\mathbb{R}^n $ is the subset

\[ P = \bigl\{a_1x_1 + a_2x_2 + \cdots + a_nx_n \bigm| 0 \leq a_1,a_2,\ldots,a_n\leq 1\bigr\}. \nonumber \]

In other words, a parallelepiped is the set of all linear combinations of $n$ vectors with coefficients in $[0,1]$. We can draw parallelepipeds using the parallelogram law for vector addition.

Example $\PageIndex{1}$: The Unit Cubte

The parallelepiped determined by the standard coordinate vectors $e_1,e_2,\ldots,e_n$ is the unit $n$-dimensional cube.

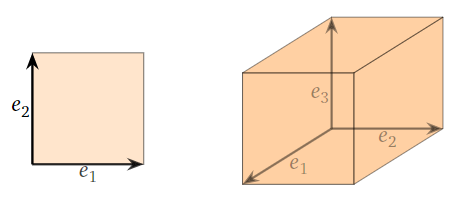
$clipboard_e85e037106e647557d69a7eef7f807287.png$

Figure $\PageIndex{1}$

Example $\PageIndex{2}$: Parallelograms

When $n = 2\text{,}$ a paralellepiped is just a paralellogram in $\mathbb{R}^2 $. Note that the edges come in parallel pairs.

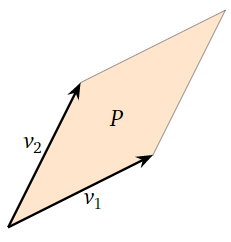
$clipboard_e795c3e4b79086124d7f8ece02f1ea5da.png$

Figure $\PageIndex{2}$

Example $\PageIndex{3}$

When $n=3\text{,}$ a parallelepiped is a kind of a skewed cube. Note that the faces come in parallel pairs.

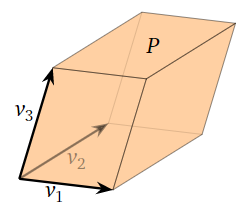
$clipboard_edcf74074ff27cd13d9f62da5ee1826b8.png$

Figure $\PageIndex{3}$

When does a parallelepiped have zero volume? This can happen only if the parallelepiped is flat, i.e., it is squashed into a lower dimension.

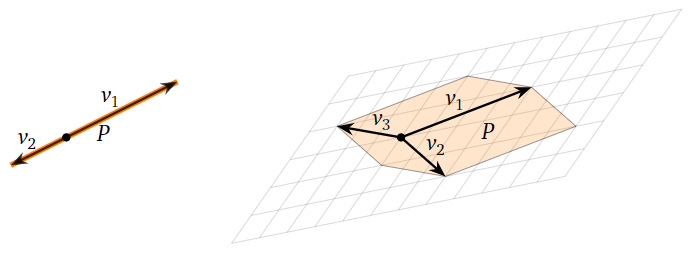
$clipboard_e3ae0654c311649ec99d986554e966479.png$

Figure $\PageIndex{4}$

This means exactly that $\{v_1,v_2,\ldots,v_n\}$ is linearly dependent, which by Corollary 4.1.1 in Section 4.1 means that the matrix with rows $v_1,v_2,\ldots,v_n$ has determinant zero. To summarize:

Key Observation $\PageIndex{1}$

The parallelepiped defined by $v_1,v_2,\ldots,v_n$ has zero volume if and only if the matrix with rows $v_1,v_2,\ldots,v_n$ has zero determinant.

Determinants and Volumes

The key observation above is only the beginning of the story: the volume of a parallelepiped is always a determinant.

Theorem $\PageIndex{1}$: Determinants and Volumes

Let $v_1,v_2,\ldots,v_n$ be vectors in $\mathbb{R}^n \text{,}$ let $P$ be the parallelepiped determined by these vectors, and let $A$ be the matrix with rows $v_1,v_2,\ldots,v_n$. Then the absolute value of the determinant of $A$ is the volume of $P\text{:}$

\[ |\det(A)| = \text{vol}(P). \nonumber \]

Proof

Since the four defining properties, Definition 4.1.1 in Section 4.1, characterize the determinant, they also characterize the absolute value of the determinant. Explicitly, $|\det|$ is a function on square matrices which satisfies these properties:

Doing a row replacement on $A$ does not change $|\det(A)|$.
Scaling a row of $A$ by a scalar $c$ multiplies $|\det(A)|$ by $|c|$.
Swapping two rows of a matrix does not change $|\det(A)|$.
The determinant of the identity matrix $I_n$ is equal to $1$.

The absolute value of the determinant is the only such function: indeed, by Recipe: Computing Determinants by Row Reducing in Section 4.1, if you do some number of row operations on $A$ to obtain a matrix $B$ in row echelon form, then

\[ |\det(A)| = \left|\frac{\text{(product of the diagonal entries of $B$)}} {\text{(product of scaling factors used)}}\right|. \nonumber \]

For a square matrix $A\text{,}$ we abuse notation and let $\text{vol}(A)$ denote the volume of the paralellepiped determined by the rows of $A$. Then we can regard $\text{vol}$ as a function from the set of square matrices to the real numbers. We will show that $\text{vol}$ also satisfies the above four properties.

For simplicity, we consider a row replacement of the form $R_n = R_n + cR_i$. The volume of a paralellepiped is the volume of its base, times its height: here the “base” is the paralellepiped determined by $v_1,v_2,\ldots,v_{n-1}\text{,}$ and the “height” is the perpendicular distance of $v_n$ from the base.

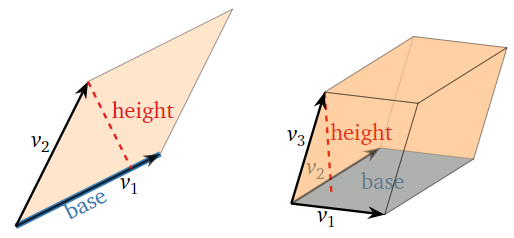
$clipboard_e71160e00c8e7b2eca7e59af5cf639fb4.png$

Figure $\PageIndex{5}$

Translating $v_n$ by a multiple of $v_i$ moves $v_n$ in a direction parallel to the base. This changes neither the base nor the height! Thus, $\text{vol}(A)$ is unchanged by row replacements.

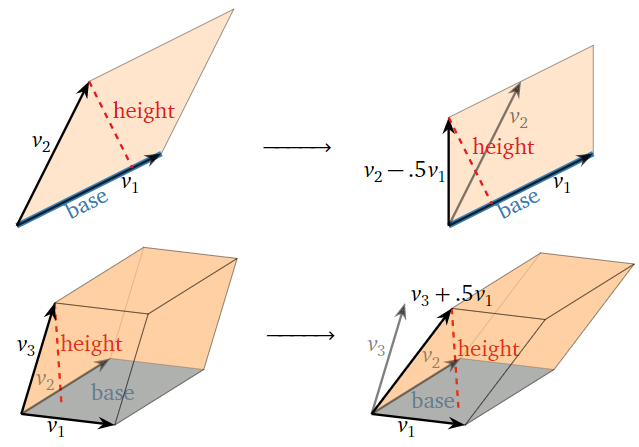
$clipboard_e29842a92b93a439261e05901e156426d.png$

Figure $\PageIndex{6}$

For simplicity, we consider a row scale of the form $R_n = cR_n.$ This scales the length of $v_n$ by a factor of $|c|\text{,}$ which also scales the perpendicular distance of $v_n$ from the base by a factor of $|c|$. Thus, $\text{vol}(A)$ is scaled by $|c|$.

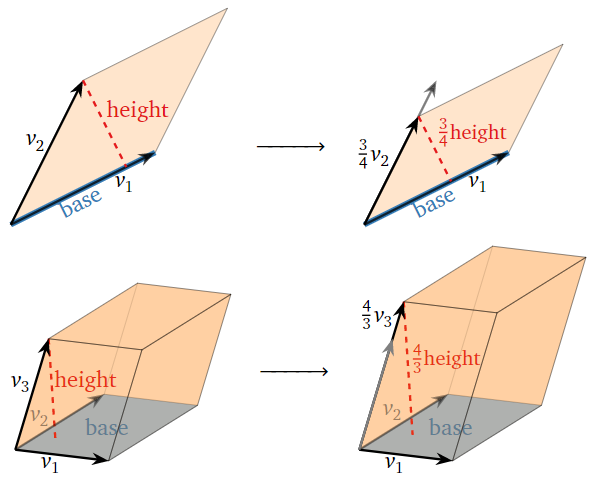
$clipboard_e2baf3c7acf633020b8fc3019ad6fae3a.png$

Figure $\PageIndex{7}$

Swapping two rows of $A$ just reorders the vectors $v_1,v_2,\ldots,v_n\text{,}$ hence has no effect on the parallelepiped determined by those vectors. Thus, $\text{vol}(A)$ is unchanged by row swaps.

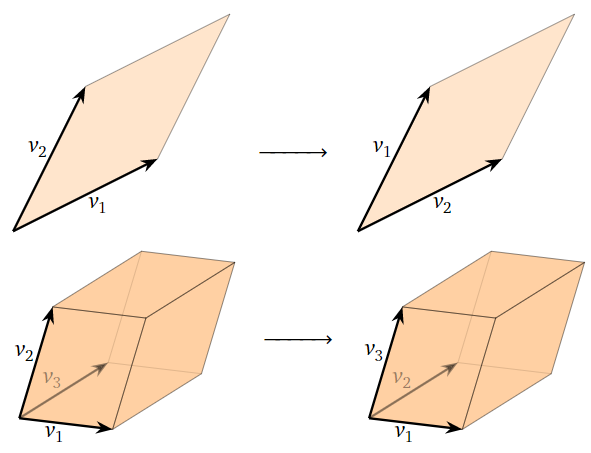
$clipboard_eef6982bf309872c979890292332ce380.png$

Figure $\PageIndex{8}$

The rows of the identity matrix $I_n$ are the standard coordinate vectors $e_1,e_2,\ldots,e_n$. The associated paralellepiped is the unit cube, which has volume $1$. Thus, $\text{vol}(I_n) = 1$.

Since $|\det|$ is the only function satisfying these properties, we have

\[ \text{vol}(P) = \text{vol}(A) = |\det(A)|. \nonumber \]

This completes the proof.

Since $\det(A) = \det(A^T)$ by the transpose property, Proposition 4.1.4 in Section 4.1, the absolute value of $\det(A)$ is also equal to the volume of the paralellepiped determined by the columns of $A$ as well.

Example $\PageIndex{4}$: Length

A $1\times 1$ matrix $A$ is just a number $\left(\begin{array}{c}a\end{array}\right)$. In this case, the parallelepiped $P$ determined by its one row is just the interval $[0,a]$ (or $[a,0]$ if $a\lt0$). The “volume” of a region in $\mathbb{R}^1 = \mathbb{R}$ is just its length, so it is clear in this case that $\text{vol}(P) = |a|$.

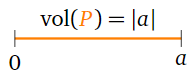
$clipboard_ec6b3c1a1c41e68276a917be470c327ce.png$

Figure $\PageIndex{9}$

Example $\PageIndex{5}$: Area

When $A$ is a $2\times 2$ matrix, its rows determine a parallelogram in $\mathbb{R}^2 $. The “volume” of a region in $\mathbb{R}^2 $ is its area, so we obtain a formula for the area of a parallelogram: it is the determinant of the matrix whose rows are the vectors forming two adjacent sides of the parallelogram.

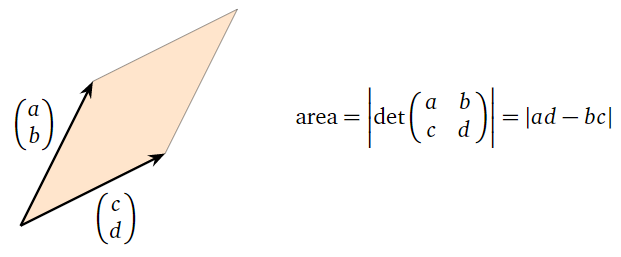
$clipboard_e2817e71743714ff0f02be6d1bc6ed6f3.png$

Figure $\PageIndex{10}$

It is perhaps surprising that it is possible to compute the area of a parallelogram without trigonometry. It is a fun geometry problem to prove this formula by hand. [Hint: first think about the case when the first row of $A$ lies on the $x$-axis.]

Example $\PageIndex{6}$

Find the area of the parallelogram with sides $(1,3)$ and $(2,-3)$.

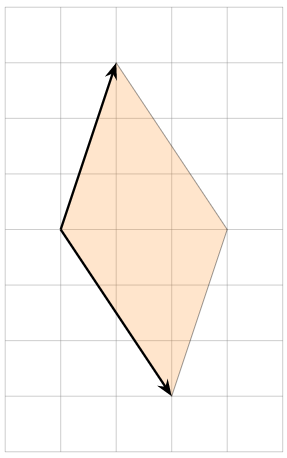
$clipboard_e9e9746c8dab7e8ba5bece83f8cad8ed3.png$

Figure $\PageIndex{11}$

Solution

The area is

\[ \left|\det\left(\begin{array}{cc}1&3\\2&-3\end{array}\right)\right| = |-3-6| = 9. \nonumber \]

Example $\PageIndex{7}$

Find the area of the parallelogram in the picture.

$clipboard_e90f92d08fdd343c40883a789a0b318f5.png$

Figure $\PageIndex{12}$

Solution

We choose two adjacent sides to be the rows of a matrix. We choose the top two:

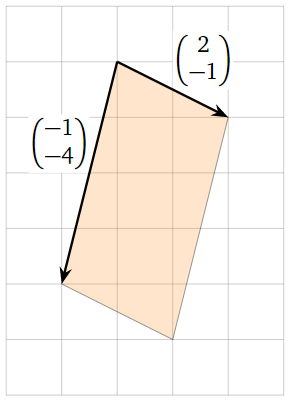
$clipboard_ec309659dca41ee107f84132467320202.png$

Figure $\PageIndex{13}$

Note that we do not need to know where the origin is in the picture: vectors are determined by their length and direction, not where they start. The area is

\[ \left|\det\left(\begin{array}{cc}-1&-4\\2&-1\end{array}\right)\right| = |1+8| = 9. \nonumber \]

Example $\PageIndex{8}$: Area of a triangle

Find the area of the triangle with vertices $(-1,-2), \,(2,-1),\,(1,3).$

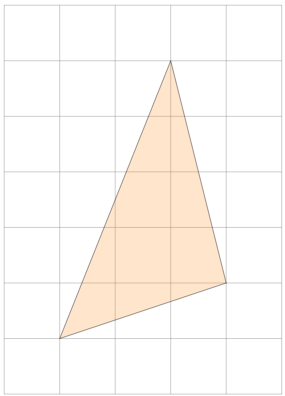
$clipboard_eb0dc0b2840b335994f22acb5dfae30ac.png$

Figure $\PageIndex{14}$

Solution

Doubling a triangle makes a paralellogram. We choose two of its sides to be the rows of a matrix.

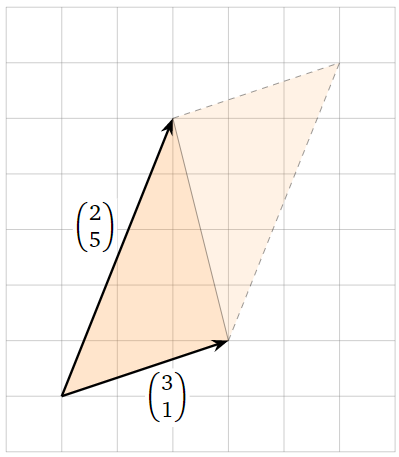
$clipboard_e2d12f4d7748e7b7df3c755e5d55163c5.png$

Figure $\PageIndex{15}$

The area of the parallelogram is

\[ \left|\det\left(\begin{array}{cc}2&5\\3&1\end{array}\right)\right| = |2-15| = 13, \nonumber \]

so the area of the triangle is $13/2$.

You might be wondering: if the absolute value of the determinant is a volume, what is the geometric meaning of the determinant without the absolute value? The next remark explains that we can think of the determinant as a signed volume. If you have taken an integral calculus course, you probably computed negative areas under curves; the idea here is similar.

Remark: Signed volumes

Theorem $\PageIndex{1}$ on determinants and volumes tells us that the absolute value of the determinant is the volume of a paralellepiped. This raises the question of whether the sign of the determinant has any geometric meaning.

A $1\times 1$ matrix $A$ is just a number $\left(\begin{array}{c}a\end{array}\right)$. In this case, the parallelepiped $P$ determined by its one row is just the interval $[0,a]$ if $a \geq 0\text{,}$ and it is $[a,0]$ if $a\lt0$. In this case, the sign of the determinant determines whether the interval is to the left or the right of the origin.

For a $2\times 2$ matrix with rows $v_1,v_2\text{,}$ the sign of the determinant determines whether $v_2$ is counterclockwise or clockwise from $v_1$. That is, if the counterclockwise angle from $v_1$ to $v_2$ is less than $180^\circ\text{,}$ then the determinant is positive; otherwise it is negative (or zero).

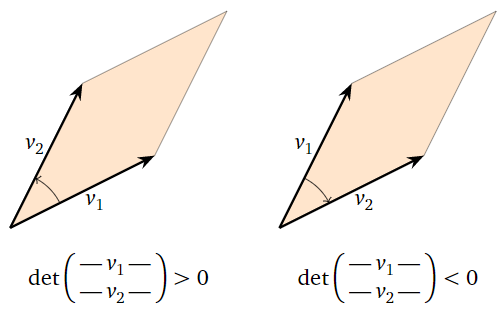
$clipboard_ea295b4d37be522353998e0e3862cb12b.png$

Figure $\PageIndex{16}$

For example, if $v_1 = {a\choose b}\text{,}$ then the counterclockwise rotation of $v_1$ by $90^\circ$ is $v_2 = {-b\choose a}$ by Example 3.3.8 in Section 3.3, and

\[ \det\left(\begin{array}{cc}a&b\\-b&a\end{array}\right) = a^2 + b^2 > 0. \nonumber \]

On the other hand, the clockwise rotation of $v_1$ by $90^\circ$ is $b\choose -a\text{,}$ and

\[ \det\left(\begin{array}{cc}a&b\\b&-a\end{array}\right) = -a^2 - b^2 \lt 0. \nonumber \]

For a $3\times 3$ matrix with rows $v_1,v_2,v_3\text{,}$ the right-hand rule determines the sign of the determinant. If you point the index finger of your right hand in the direction of $v_1$ and your middle finger in the direction of $v_2\text{,}$ then the determinant is positive if your thumb points roughly in the direction of $v_3\text{,}$ and it is negative otherwise.

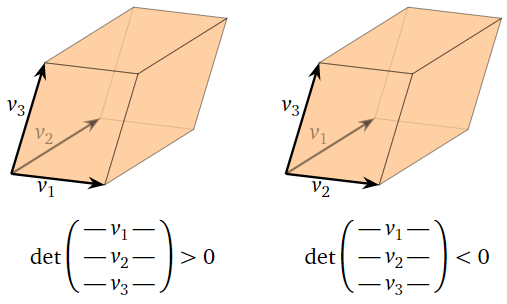
$clipboard_e15c233c79730c48ddde8f9d6dca57b58.png$

Figure $\PageIndex{17}$

In higher dimensions, the notion of signed volume is still important, but it is usually defined in terms of the sign of a determinant.

Volumes of Regions

Let $A$ be an $n\times n$ matrix with columns $v_1,v_2,\ldots,v_n\text{,}$ and let $T\colon\mathbb{R}^n \to\mathbb{R}^n $ be the associated matrix transformation, Definition 3.1.3 in Section 3.1, $T(x)=Ax$. Then $T(e_1)=v_1$ and $T(e_2)=v_2\text{,}$ so $T$ takes the unit cube $C$ to the parallelepiped $P$ determined by $v_1,v_2,\ldots,v_n\text{:}$

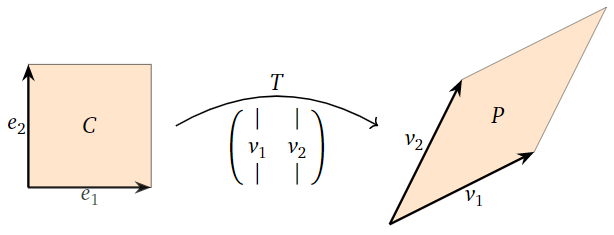
$clipboard_eedecb358654be10e0bfd9ded6b278c2c.png$

Figure $\PageIndex{18}$

Since the unit cube has volume $1$ and its image has volume $|\det(A)|\text{,}$ the transformation $T$ scaled the volume of the cube by a factor of $|\det(A)|$. To rephrase:

Note $\PageIndex{1}$

If $A$ is an $n\times n$ matrix with corresponding matrix transformation $T\colon\mathbb{R}^n \to\mathbb{R}^n \text{,}$ and if $C$ is the unit cube in $\mathbb{R}^n \text{,}$ then the volume of $T(C)$ is $|\det(A)|.$

The notation $T(S)$ means the image of the region $S$ under the transformation $T$. In set builder notation, Note 2.2.3 in Section 2.2, this is the subset

\[ T(S) = \bigl\{T(x)\mid x \text{ in } S\bigr\}. \nonumber \]

In fact, $T$ scales the volume of any region in $\mathbb{R}^n $ by the same factor, even for curvy regions.

Theorem $\PageIndex{2}$

Let $A$ be an $n\times n$ matrix, and let $T\colon\mathbb{R}^n \to\mathbb{R}^n $ be the associated matrix transformation $T(x)=Ax$. If $S$ is any region in $\mathbb{R}^n \text{,}$ then

\[ \text{vol}(T(S))=|\det(A)|\cdot\text{vol}(S). \nonumber \]

Proof

Let $C$ be the unit cube, let $v_1,v_2,\ldots,v_n$ be the columns of $A\text{,}$ and let $P$ be the paralellepiped determined by these vectors, so $T(C) = P$ and $\text{vol}(P) = |\det(A)|$. For $\epsilon > 0$ we let $\epsilon C$ be the cube with side lengths $\epsilon\text{,}$ i.e., the paralellepiped determined by the vectors $\epsilon e_1,\epsilon e_2,\ldots,\epsilon e_n\text{,}$ and we define $\epsilon P$ similarly. By the second defining property, $T$ takes $\epsilon C$ to $\epsilon P$. The volume of $\epsilon C$ is $\epsilon^n$ (we scaled each of the $n$ standard vectors by a factor of $\epsilon$) and the volume of $\epsilon P$ is $\epsilon^n|\det(A)|$ (for the same reason), so we have shown that $T$ scales the volume of $\epsilon C$ by $|\det(A)|$.

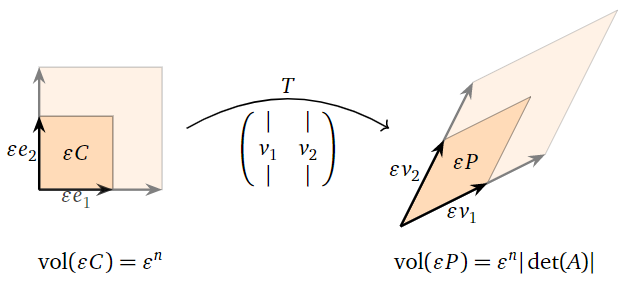
$clipboard_e5c48c9f5250c5dbbe9b2f31c21e4b457.png$

Figure $\PageIndex{19}$

By the first defining property, Definition 3.3.1 in Section 3.3, the image of a translate of $\epsilon C$ is a translate of $\epsilon P\text{:}$

\[ T(x + \epsilon C) = T(x) + \epsilon T(C) = T(x) + \epsilon P. \nonumber \]

Since a translation does not change volumes, this proves that $T$ scales the volume of a translate of $\epsilon C$ by $|\det(A)|$.

At this point, we need to use techniques from multivariable calculus, so we only give an idea of the rest of the proof. Any region $S$ can be approximated by a collection of very small cubes of the form $x + \epsilon C$. The image $T(S)$ is then approximated by the image of this collection of cubes, which is a collection of very small paralellepipeds of the form $T(x) + \epsilon P$.

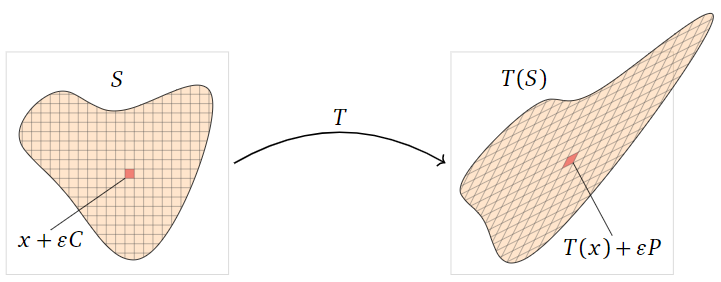
$clipboard_e11eba8c79aa78c611b71e5120509133b.png$

Figure $\PageIndex{20}$

The volume of $S$ is closely approximated by the sum of the volumes of the cubes; in fact, as $\epsilon$ goes to zero, the limit of this sum is precisely $\text{vol}(S)$. Likewise, the volume of $T(S)$ is equal to the sum of the volumes of the paralellepipeds, take in the limit as $\epsilon\to 0$. The key point is that the volume of each cube is scaled by $|\det(A)|$. Therefore, the sum of the volumes of the paralellepipeds is $|\det(A)|$ times the sum of the volumes of the cubes. This proves that $\text{vol}(T(S)) = |\det(A)|\text{vol}(S).$

Example $\PageIndex{9}$

Let $S$ be a half-circle of radius $1\text{,}$ let

\[ A = \left(\begin{array}{cc}1&2\\2&1\end{array}\right), \nonumber \]

and define $T\colon\mathbb{R}^2 \to\mathbb{R}^2 $ by $T(x)=Ax$. What is the area of $T(S)\text{?}$

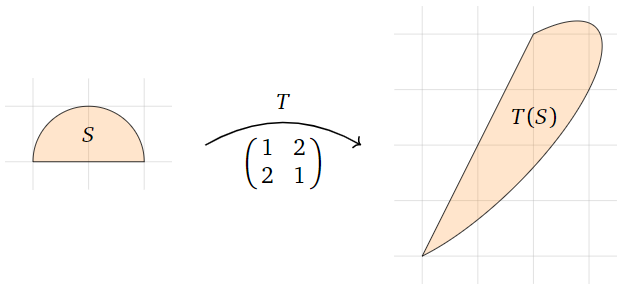
$clipboard_ec1847dde138b858fc1b133c6610ca44f.png$

Figure $\PageIndex{21}$

Solution

The area of the unit circle is $\pi\text{,}$ so the area of $S$ is $\pi/2$. The transformation $T$ scales areas by a factor of $|\det(A)| = |1 - 4| = 3\text{,}$ so

\[ \text{vol}(T(S)) = 3\text{vol}(S) = \frac{3\pi}2. \nonumber \]

Example $\PageIndex{10}$: Area of an ellipse

Find the area of the interior $E$ of the ellipse defined by the equation

\[ \left(\frac{2x-y}{2}\right)^2 + \left(\frac{y+3x}{3}\right)^2 = 1. \nonumber \]

Solution

This ellipse is obtained from the unit circle $X^2+Y^2=1$ by the linear change of coordinates

\[ \begin{split} X \amp= \frac{2x-y}2 \\ Y \amp= \frac{y+3x}3. \end{split} \nonumber \]

In other words, if we define a linear transformation $T\colon\mathbb{R}^2 \to\mathbb{R}^2 $ by

\[ T\left(\begin{array}{c}x\\y\end{array}\right) = \left(\begin{array}{c}(2x-y)/2 \\ (y+3x)/3\end{array}\right), \nonumber \]

then $T{x\choose y}$ lies on the unit circle $C$ whenever $x\choose y$ lies on $E$.

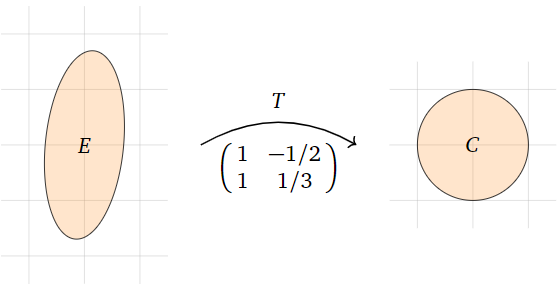
$clipboard_e842a398db5b34f989d7bc3b698a93289.png$

Figure $\PageIndex{22}$

We compute the standard matrix $A$ for $T$ by evaluating on the standard coordinate vectors:

\[ T\left(\begin{array}{c}1\\0\end{array}\right) = \left(\begin{array}{c}1\\1\end{array}\right) \qquad T\left(\begin{array}{c}0\\1\end{array}\right) = \left(\begin{array}{c}-1/2 \\ 1/3\end{array}\right) \quad\implies\quad A = \left(\begin{array}{cc}1&-1/2 \\ 1&1/3\end{array}\right). \nonumber \]

Therefore, $T$ scales areas by a factor of $|\det(A)| = |\frac13+\frac12| = \frac56.$ The area of the unit circle is $\pi\text{,}$ so

\[ \pi = \text{vol}(C) = \text{vol}(T(E)) = |\det(A)|\cdot\text{vol}(E) = \frac56\text{vol}(E), \nonumber \]

and thus the area of $E$ is $6\pi/5$.

Remark: Multiplicativity of $|\det|\,$

The above Theorem $\PageIndex{2}$ also gives a geometric reason for multiplicativity of the (absolute value of the) determinant. Indeed, let $A$ and $B$ be $n\times n$ matrices, and let $T,U\colon\mathbb{R}^n \to\mathbb{R}^n $ be the corresponding matrix transformations. If $C$ is the unit cube, then

\[ \begin{split} \text{vol}\bigl(T\circ U(C)\bigr) = \text{vol}\bigl(T(U(C))\bigr) \amp= |\det(A)|\text{vol}(U(C)) \\ \amp= |\det(A)|\cdot|\det(B)|\text{vol}(C) \\ \amp= |\det(A)|\cdot|\det(B)|. \end{split} \nonumber \]

On the other hand, the matrix for the composition $T\circ U$ is the product $AB\text{,}$ so

\[ \text{vol}\bigl(T\circ U(C)\bigr) = |\det(AB)|\text{vol}(C) = |\det(AB)|. \nonumber \]

Search

Definition \(\PageIndex{1}\): Paralellepiped

Example \(\PageIndex{1}\): The Unit Cubte

Example \(\PageIndex{2}\): Parallelograms

Example \(\PageIndex{3}\)

Key Observation \(\PageIndex{1}\)

Theorem \(\PageIndex{1}\): Determinants and Volumes

Example \(\PageIndex{4}\): Length

Example \(\PageIndex{5}\): Area

Example \(\PageIndex{6}\)

Solution

Example \(\PageIndex{7}\)

Solution

Example \(\PageIndex{8}\): Area of a triangle

Solution

Remark: Signed volumes

Note \(\PageIndex{1}\)

Theorem \(\PageIndex{2}\)

Example \(\PageIndex{9}\)

Solution

Example \(\PageIndex{10}\): Area of an ellipse

Solution

Remark: Multiplicativity of \(|\det|\,\)