4.2: Hyperplanes
- Page ID
- 1850
Vectors in \(\mathbb{R}^{n}\) can be hard to visualize. However, familiar objects like lines and planes still make sense: The line \(L\) along the direction defined by a vector \(v\) and through a point \(P\) labeled by a vector \(u\) can be written as $$L=\{ u + tv | t \in \mathbb{R} \}\, .$$
Sometimes, since we know that a point \(P\) corresponds to a vector, we will be lazy and just write \(L=\{P + tv | t \in \mathbb{R} \}\).
\(\left\{ \begin{pmatrix}1\\2\\3\\4\end{pmatrix} + t\begin{pmatrix}1\\0\\0\\0\end{pmatrix} \middle\arrowvert t \in \mathbb{R} \right\}\) describes a line in \(\mathbb{R}^{4}\) parallel to the \(x_1\)-axis.
Given two non-zero vectors \(u,v\), they will \(\textit{usually}\) determine a plane,
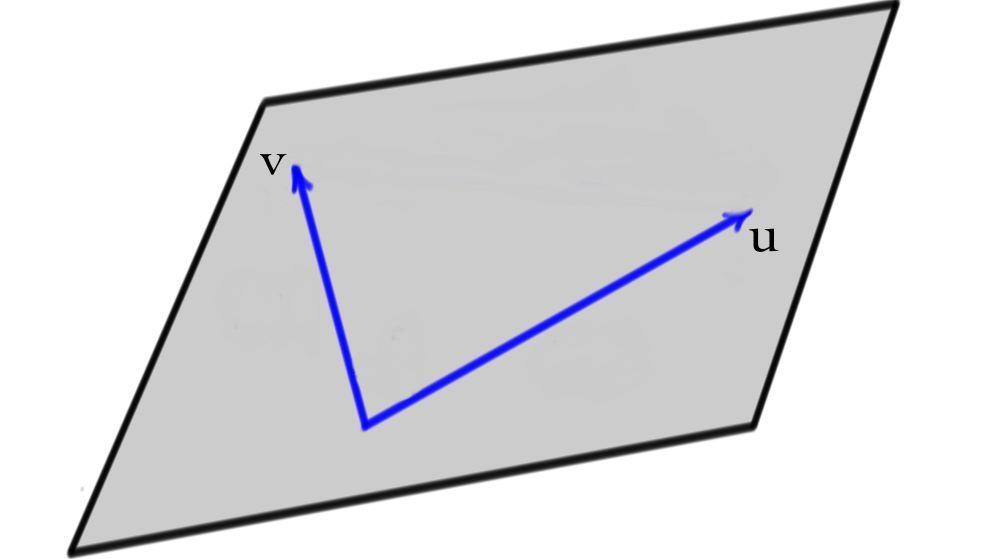
unless both vectors are in the same line, in which case, one of the vectors is a scalar multiple of the other. The sum of \(u\) and \(v\) corresponds to laying the two vectors head-to-tail and drawing the connecting vector. If \(u\) and \(v\) determine a plane, then their sum lies in the plane determined by \(u\) and \(v\).
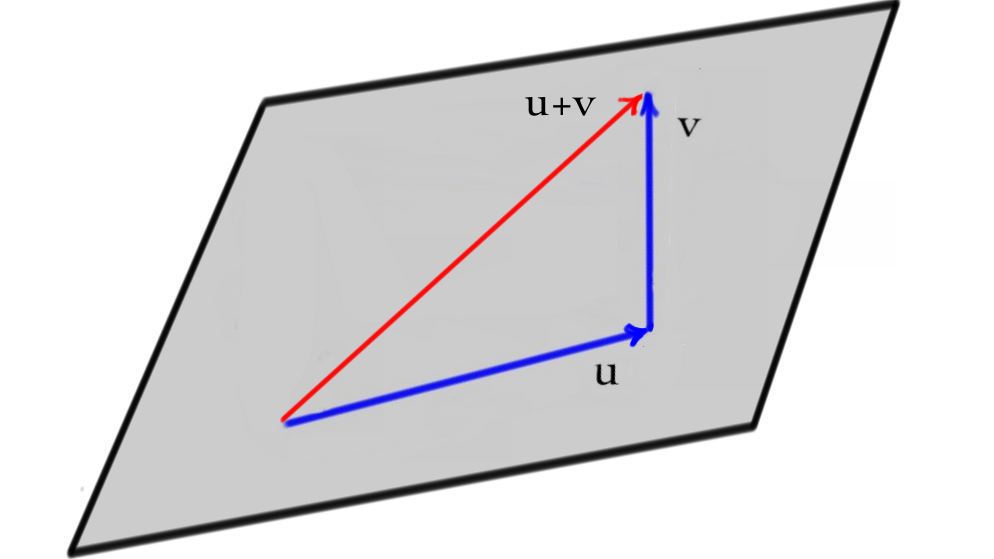
The plane determined by two vectors \(u\) and \(v\) can be written as $$\{ P + su + tv | s, t \in \mathbb{R} \}\, .$$
\[\left\{ \begin{pmatrix}3\\1\\4\\1\\5\\9\end{pmatrix} + s\begin{pmatrix}1\\0\\0\\0\\0\\0\end{pmatrix} + t\begin{pmatrix}0\\1\\0\\0\\0\\0\end{pmatrix} \middle\arrowvert s, t \in \mathbb{R} \right\}$$ describes a plane in 6-dimensional space parallel to the \(xy\)-plane.
We can generalize the notion of a plane with the following recursive definition. (That is, infinitely many things are defined in the following line.)
Definition
A set of \(k\) vectors \(v_{1}, \ldots, v_{k}\) in \(\mathbb{R}^{n}\) with \(k\leq n\) determines a \(k\)-dimensional \(\textit{hyperplane}\), unless any of the vectors \(v_{i}\) lives in the same hyperplane determined by the other vectors. If the vectors do determine a \(k\)-dimensional hyperplane, then any point in the hyperplane can be written as:
\[ \left\{ P + \sum_{i=1}^{k} \lambda_{i}v_{i}\, |\, \lambda_{i} \in \mathbb{R} \right\} \]
When the dimension \(k\) is not specified, one usually assumes that \(k=n-1\) for a hyperplane inside \(\mathbb{R}^{n}\).
Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


