1.4: Review Problems
- Page ID
- 1723
1. Problems A, B, and C of example 2 can all be written as \(Lv=w\) where $$L:V \longrightarrow W\, ,$$ (read this as \(L\) maps the set of vectors \(V\) to the set of vectors \(W\)). For each case write down the sets \(V\) and \(W\) where the vectors \(v\) and \(w\) come from.
2. Torque is a measure of "rotational force''. It is a vector whose direction is the (preferred) axis of rotation. Upon applying a force \(F\) on an object at point \(r\) the torque \(\tau\) is the cross product \(r\times F=\tau\).
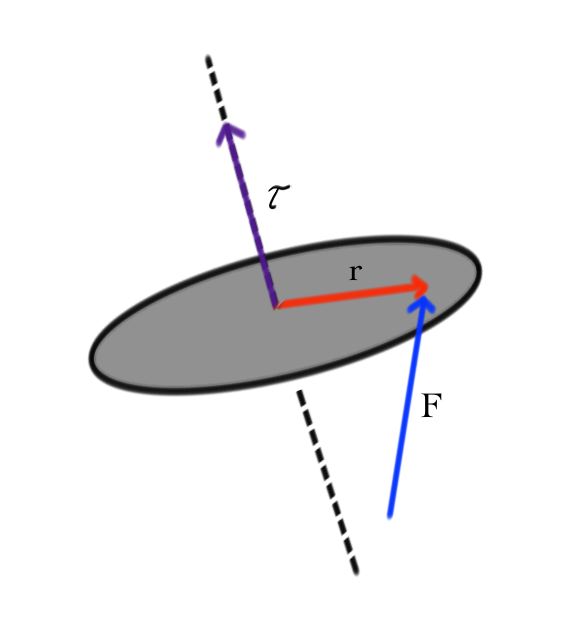
Lets find the force \(F\) (a vector) must one apply to a wrench lying along the vector
\(r=\begin{pmatrix}1 \\ 1\\ 0\end{pmatrix}\) ft,
to produce a torque \(\begin{pmatrix}0\\0 \\ 1\end{pmatrix}\) ft lb:
- Find a solution by writing out this equation with \(F=\begin{pmatrix} a \\ b \\ c\end{pmatrix}.\) (Hint: Guess and check that a solution with \(a=0\) exists).
- Add \(\begin{pmatrix}1 \\ 1 \\ 0\end{pmatrix}\) to your solution and check that the result is a solution.
- Give a physics explanation why there can be two solutions, and argue that there are, in fact, infinitely many solutions.
- Set up a system of three linear equations with the three components of \(F\) as the variables which describes this situation. What happens if you try to solve these equations by substitution?
3. The function \(P(t)\) gives gas prices (in units of dollars per gallon) as a function of \(t\) the year, and \(g(t)\) is the gas consumption rate measured in gallons per year by an average driver as a function of their age. Assuming a lifetime is 100 years, what function gives the total amount spent on gas during the lifetime of an individual born in an arbitrary year \(t\)? Is the operator that maps \(g\) to this function linear?
4. The differential equation (DE) $$\frac{d}{dt} f=2f$$ says that the rate of change of \(f\) is proportional to \(f\). It describes exponential growth because $$f(t)=f(0)e^{2t}$$ satisfies the DE for any number \(f(0)\). The number 2 in the DE is called the constant of proportionality.
A similar DE $$\frac{d}{dt}f=\frac{2}{t}f$$ has a time-dependent "constant of proportionality''.
- Do you think that the second DE describes exponential growth?
- Write both DEs in the form \(Df=0\) with \(D\) a linear operator.
5. Pablo is a nutritionist who knows that oranges always have twice as much sugar as apples. When considering the sugar intake of schoolchildren eating a barrel of fruit, he represents the barrel like so:

Find a linear operator relating Pablo's representation to the ``everyday'' representation in terms of the number of apples and number of oranges. Write your answer as a matrix. Hint: Let \(\lambda\) represent the amount of sugar in each apple.
6. \(\textit {Matrix Multiplication:}\) Let \(M\) and \(N\) be matrices
\[
M= \begin{pmatrix}
a &b \\
c &d
\end{pmatrix}\, \mbox{ and }
N= \begin{pmatrix}
e &f \\
g &h
\end{pmatrix}\, ,
\]
and \(v\) the vector
\[
v= \begin{pmatrix}
x \\
y \end{pmatrix}\, .
\]
If we first apply \(N\) and then \(M\) to \(v\) we obtain the vector \(MNv\).
- Show that the composition of matrices \(MN\) is also a linear operator.
- Write out the components of the matrix product \(MN\) in terms of the components of \(M$ and the components of \(N\). \(\textit {Hint}:\) use the \hyperlink{ch1vecmult}{general rule} for multiplying a 2-vector by a \(2\times2\) matrix.
- Try to answer the following common question, "Is there any sense in which these rules for matrix multiplication are unavoidable, or are they just a notation that could be replaced by some other notation?"
- Generalize your multiplication rule to \(3\times 3\) matrices.
7. \(\textit{Diagonal matrices:}\) A matrix \(M\) can be thought of as an array of numbers \(m^i_j\), known as matrix entries, or matrix components, where \(i\) and \(j\) index row and column numbers, respectively. Let
$$
M=\begin{pmatrix}1&2\\3&4\end{pmatrix}=\big(m^i_j\big)\, .
$$
Compute \(m^1_1\), \(m^1_2\), \(m^2_1\) and \(m^2_2\).
The matrix entries \(m^i_i\) whose row and column numbers are the same are called the \(\textit {diagonal}\)
of \(M\). Matrix entries \(m^i_j\) with \(i\neq j\) are called \(\textit {off-diagonal}\). How many diagonal entries does an \(n\times n\) matrix have? How many off-diagonal entries does an \(n\times n\) matrix have?
If all the off-diagonal entries of a matrix vanish, we say that the matrix is diagonal. Let
$$
D=\begin{pmatrix}\lambda&0\\0&\mu\end{pmatrix}\quad \mbox{and}\quad D'=\begin{pmatrix}\lambda'&0\\0&\mu'\end{pmatrix}\, .
\]
Are these matrices diagonal and why? Use the rule you found in problem 6 to compute
the matrix products \(DD'\) and \(D'D\). What do you observe? Do you think the same property holds for arbitrary matrices? What about products where only one of the matrices is diagonal?
8. Find the linear operator that takes in vectors from \(n\)-space and gives out vectors from \(n\)-space in such a way that whatever you put in, you get exactly the same thing out. Show that it is unique. Can you write this operator as a matrix? \(\textit {Hint:}\) To show something is unique, it is usually best to begin by pretending that it isn't, and then showing that this leads to a nonsensical conclusion. In mathspeak--\(\textit {proof by contradiction}\).
9. Consider the set \(S=\{*, \star, \# \}\).
It contains just 3 elements, and has no ordering;
\(\{*, \star, \# \}= \{ \# , \star, * \}\) \(\textit {etc}\).
(In fact the same is true for \(\{1,2,3\}=\{2,3,1\}\) \(\textit {etc}\), although we could make this an \(\textit {ordered set}\) using \(3>2>1\).)
- Invent a function with domain \(\{*, \star, \# \}\) and co\-domain \(\Re\). (Remember that the \(\textit {domain}\) of a function is the set of all its allowed inputs and the \(\textit {codomain}\) (or \(\textit {target space}\)) is the set where the outputs can live. A function is specified by assigning exactly one codomain element to each element of the domain.)
- Choose an ordering on \(\{*, \star, \# \}\), and then use it to write your function from part (i) as a triple of numbers.
- Choose a new ordering on \(\{*, \star, \# \}\) and then write your function from part(i) as a triple of numbers.
- Your answers for parts (ii) and (iii) are different yet represent the same function -- explain!
Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


