14.6: Orthogonal Complements

Let \(U\) and \(V\) be subspaces of a vector space \(W\). In review exercise 6 you are asked to show that \(U\cap V\) is a subspace of \(W\), and that \(U\cup V\) is not a subspace. However, \(span (U\cup V)\) is certainly a subspace, since the span of \(\textit{any}\) subset of a vector space is a subspace. Notice that all elements of \(span (U\cup V)\) take the form \(u+v\) with \(u\in U\) and \(v\in V\). We call the subspace \(U+V:=span (U\cup V) = \{u+v | u\in U, v\in V \}\) the \(\textit{sum}\) of \(U\) and \(V\). Here, we are not adding vectors, but vector spaces to produce a new vector space!

Definition: Direct sum

Given two subspaces \(U\) and \(V\) of a space \(W\) such that $$U\cap V=\{0_{W}\}\, ,$$ the \(\textit{direct sum}\) of \(U\) and \(V\) is defined as:

\[ U \oplus V = span (U\cup V)= \{u+v | u\in U, v\in V \}. \]

Remark: When \(U\cap V= \{0_{W}\}\), \(U+V=U\oplus V\).

The direct sum has a very nice property:

Theorem

If \(w\in U\oplus V\) then the expression \(w=u+v\) is unique. That is, there is only one way to write \(w\) as the sum of a vector in \(U\) and a vector in \(V\).

Proof

Suppose that \(u+v=u'+v'\), with \(u,u'\in U\), and \(v,v' \in V\). Then we could express \(0=(u-u')+(v-v')\). Then \((u-u')=-(v-v')\). Since \(U\) and \(V\) are subspaces, we have \((u-u')\in U\) and \(-(v-v')\in V\). But since these elements are equal, we also have \((u-u')\in V\). Since \(U\cap V=\{0\}\), then \((u-u')=0\). Similarly, \((v-v')=0\). Therefore \(u=u'\) and \(v=v'\), proving the theorem.

Given a subspace \(U\) in \(W\), how can we write \(W\) as the direct sum of \(U\) and \(\textit{something}\)? There is not a unique answer to this question as can be seen from this picture of subspaces in \(W=\mathbb{R}^{3}\):

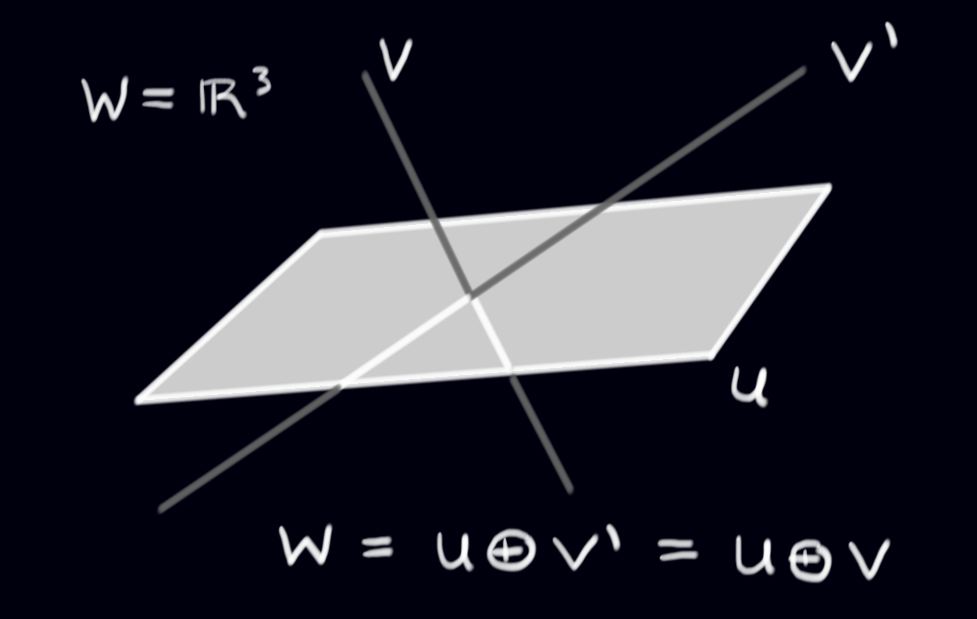
\(\square\)

The general definition is as follows:

Definition

Given a subspace \(U\) of a vector space \(W\), define \(U^{\perp} = \big\{w\in W | w\cdot u=0 \textit{ for all } u\in U\big\}\, .\)}

Remark: The set \(U^{\perp}\) (pronounced "\(U\)-perp'') is the set of all vectors in \(W\) orthogonal to \(\textit{every}\) vector in \(U\). This is also often called the orthogonal complement of \(U\).

Example \(\PageIndex{1}\):

Consider any plane \(P\) through the origin in \(\Re^{3}\). Then \(P\) is a subspace, and \(P^{\perp}\) is the line through the origin orthogonal to \(P\). For example, if \(P\) is the \(xy\)-plane, then

\[ \Re^{3}=P\oplus P^{\perp}=\{(x,y,0)| x,y\in \Re \} \oplus \{(0,0,z)| z\in \Re \}.\]

Theorem

Let \(U\) be a subspace of a finite-dimensional vector space \(W\). Then the set \(U^{\perp}\) is a subspace of \(W\), and \(W=U\oplus U^{\perp}\).

Proof

First, to see that \(U^{\perp}\) is a subspace, we only need to check closure, which requires a simple check: Suppose \(v,w\in U^{\perp}\), then we know

\[v\cdot u = 0 = w\cdot u \quad (\forall u\in U)\, .\]

Hence

\[\Rightarrow u\cdot(\alpha v+\beta w)= \alpha u\cdot v + \beta u\cdot w =0\quad (\forall u\in U)\, ,$$

and so \(\alpha v+\beta w\in U^{\perp}\).

Next, to form a direct sum between \(U\) and \(U\perp\) we need to show that \(U\cap U^{\perp}=\{0\}\). This holds because if \(u\in U\) and \(u\in U^{\perp}\) it follows that

\[u\cdot u = 0 \Leftrightarrow u=0.\]

Finally, we show that any vector \(w\in W\) is in \(U\oplus U^{\perp}\). (This is where we use the assumption that \(W\) is finite-dimensional.) Let \(e_{1}, \ldots, e_{n}\) be an orthonormal basis for \(W\). Set:

\begin{eqnarray*}
u\ &=&(w\cdot e_{1})e_{1} + \cdots + (w\cdot e_{n})e_{n} \in U\, ,\\
u^{\perp}&=& w-u\, .
\end{eqnarray*}

It is easy to check that \(u^{\perp} \in U^{\perp}\) (see the Gram-Schmidt procedure). Then \(w=u+u^{\perp}\), so \(w\in U\oplus U^{\perp}\), and we are done.

\(\square\)

Example \(\PageIndex{1}\):

Consider any line \(L\) through the origin in \(\Re^{4}\). Then \(L\) is a subspace, and \(L^{\perp}\) is a \(3\)-dimensional subspace orthogonal to \(L\). For example, let \(L=span \{ (1,1,1,1)\}\) be a line in \(\Re^{4}.\) Then \(L^{\perp}\) is given by

\begin{eqnarray*}
L^{\perp}&=&\{(x,y,z,w) \mid x,y,z,w \in \Re \textit{ and } (x,y,z,w) \cdot (1,1,1,1)=0\} \\
&=&\{(x,y,z,w) \mid x,y,z,w \in \Re \textit{ and } x,y,z,w=0\}.
\end{eqnarray*}

It is easy to check that

\[
\left\{
v_{1}=\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}, v_{2}=\begin{pmatrix}1\\0\\-1\\0\end{pmatrix}, v_{3}=\begin{pmatrix}1\\0\\0\\-1\end{pmatrix} \right \}\, ,
$$

forms a basis for \(L^{\perp}\). We use Gram-Schmidt to find an orthogonal basis for \(L^{\perp}\):

First, we set \(v_{1}^{\perp}=v_{1}\). Then

\begin{eqnarray*}
v_{2}^{\perp}&=&\begin{pmatrix}1\\0\\-1\\0\end{pmatrix}-\frac{1}{2}\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}
=\begin{pmatrix}\frac{1}{2}\\ \frac{1}{2} \\-1\\ 0 \end{pmatrix},\\
v_{3}^{\perp}&=&\begin{pmatrix} 1\\0\\0\\-1\end{pmatrix} -\frac{1}{2}\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}-\frac{1/2}{3/2}
\begin{pmatrix} \frac{1}{2}\\ \frac{1}{2}\\-1\\0\end{pmatrix} =\begin{pmatrix} \frac{1}{3}\\\frac{1}{3}\\\frac{1}{3}\\-1\end{pmatrix}.
\end{eqnarray*}

So the set \[\left\{ (1,-1,0,0), \left(\frac{1}{2},\frac{1}{2},-1,0\right), \left(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1\right) \right\} \] is an orthogonal basis for \(L^{\perp}\). We find an orthonormal basis for \(L^{\perp}\) by dividing each basis vector by its length:

\[
\left\{
\left( \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}},0,0 \right),
\left( \frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, -\frac{2}{\sqrt{6}},0 \right),
\left( \frac{\sqrt{3}}{6}, \frac{\sqrt{3}}{6}, \frac{\sqrt{3}}{6}, -\frac{\sqrt{3}}{2} \right)
\right\}.
\]

Moreover, we have

\[Re^{4}=L \oplus L^{\perp} = \{(c,c,c,c) \mid c \in \Re\} \oplus \{(x,y,z,w) \mid x,y,z,w \in \Re,\, x+y+z+w=0\}.\]

Notice that for any subspace \(U\), the subspace \((U^{\perp})^{\perp}\) is just \(U\) again. As such, \(\perp\) is an \(\textit{involution}\) on the set of subspaces of a vector space. (An involution is any mathematical operation which performed twice does nothing.)

Contributor

• David Cherney, Tom Denton, and Andrew Waldron (UC Davis)