9.1: Introduction to Cardinality

In this chapter, we will explore the notion of cardinality, which formalizes what it means for two sets to be the same “size”.

What does it mean for two sets to have the same “size"? If the sets are finite, this is easy: just count how many elements are in each set. Another approach would be to pair up the elements in each set and see if there are any left over. In other words, check to see if there is a one-to-one correspondence (i.e., bijection) between the two sets.

But what if the sets are infinite? For example, consider the set of natural numbers \(\mathbb{N}\) and the set of even natural numbers \(2\mathbb{N}:= \{2n\mid n\in \mathbb{N}\}\). Clearly, \(2\mathbb{N}\) is a proper subset of \(\mathbb{N}\). Moreover, both sets are infinite. In this case, you might be thinking that \(\mathbb{N}\) is “larger than" \(2\mathbb{N}\). However, it turns out that there is a one-to-one correspondence between these two sets. In particular, consider the function \(f:\mathbb{N}\to 2\mathbb{N}\) defined via \(f(n)=2n\). It is easily verified that \(f\) is both injective and surjective. In this case, mathematics has determined that the right viewpoint is that \(\mathbb{N}\) and \(2\mathbb{N}\) do have the same “size". However, it is clear that “size" is a bit too imprecise when it comes to infinite sets. We need something more rigorous.

Definition 9.1. Let \(A\) and \(B\) be sets. We say that \(A\) and \(B\) have the same cardinality if there exists a bijection between \(A\) and \(B\). In this case, we write \(card(A)=card(B)\).

Note that we have not defined \(card(A)\) by itself. Doing so would not be too difficult for finite sets, but making such a notation precise in general is tricky business. When we write \(card(A)=card(B)\) (and later \(card(A)\leq card(B)\) and \(card(A)<card(B)\)), we are asserting the existence of a certain type of function from \(A\) to \(B\).

If \(f\) is a bijection from \(A\) to \(B\), then by Theorem 8.77, \(f^{-1}\) is a bijection from \(B\) to \(A\). Either one of these functions can be utilized to prove that \(card(A)=card(B)\). This idea is worth keeping in mind as you tackle problems in this chapter. In particular, you might have an easier time creating a bijection between two sets in one direction over the other. This is often a limitation of the human mind as to opposed to some fundamental mathematical difficulty.

Example 9.2. Let \(A=\{1,2,3,4,5\}\) and \(B=\{\text{apple},\text{banana},\text{cherry},\text{dragon fruit},\text{elderberry}\}\). The function \(f:A\to B\) given by \[f=\{(1,\text{apple}),(2,\text{banana}),(3,\text{cherry}),(4,\text{dragon fruit}),(5,\text{elderberry})\}\] is a bijection from \(A\) to \(B\), and hence \(card(A)=card(B)\). Note that this is not the only bijection from \(A\) to \(B\). In fact, there are \(5!=120\) bijections from \(A\) to \(B\), one of which is the function \(f\) we defined above. The inverse of each bijection from \(A\) to \(B\) is a bijection from \(B\) to \(A\). We could also use any of of these bijections to verify that \(card(A)=card(B)\).

Example 9.3. Define \(f:\mathbb{Z}\to 6\mathbb{Z}\) via \(f(n)=6n\). It is easily verified that \(f\) is both injective and surjective, and hence \(card(\mathbb{Z})=card(6\mathbb{Z})\). We could also utilize the inverse function \(f^{-1}:6\mathbb{Z}\to \mathbb{Z}\) given by \(f^{-1}(n)=\frac{1}{6}n\) to show that \(\mathbb{Z}\) and \(6\mathbb{Z}\) have the same cardinality.

Example 9.4. Let \(\mathbb{R}^+\) denote the set of positive real numbers and define \(f:\mathbb{R}\to \mathbb{R}^+\) via \(f(x)=e^x\). As you are likely familiar with, this exponential function is a bijection, and so \(card(\mathbb{R})=card(\mathbb{R}^+)\). Similar to the previous example, we could also use the inverse function \(f^{-1}:\mathbb{R}^+\to \mathbb{R}\) given by \(f^{-1}(x)=\ln(x)\) to show that these two sets have the same cardinality.

The previous two examples illustrate an important distinction between finite sets and infinite sets, namely infinite sets can be in bijection with proper subsets of themselves! Theorems 9.23 and 9.31 will make this idea explicit.

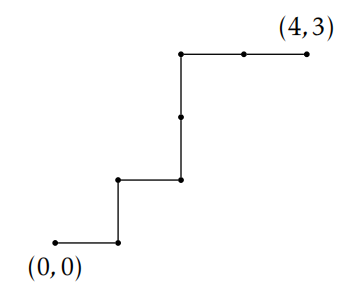
Example 9.5. Let \(m,n\in\mathbb{N}\cup\{0\}\). A North-East lattice path from \((0,0)\) to \((m,n)\) is path in the plane from \((0,0)\) to \((m,n)\) consisting only steps either one unit North or one unit East. Note that every lattice path from \((0,0)\) to \((m,n)\) consists of a total of \(m+n\) steps. Figure 9.1 shows a North-East lattice path from \((0,0)\) to \((4,3)\). Let \(\mathcal{L}_{m,n}\) denote the set of North-East paths from \((0,0)\) to \((m,n)\). For example, the North-East lattice path given in Figure 9.1 is an element of \(\mathcal{L}_{4,3}\). A binary string of length \(k\) is an ordered list of consisting of \(k\) entries where each entry is either 0 or 1. For example, \(0101100\) and \(0101001\) are two different binary strings of length 7. Let \(\mathcal{S}_k\) denote the set of binary strings of length \(k\). For example, \(\mathcal{S}_3=\{000, 100,010,001,110,101,011,111\}\). We claim that there is a bijection between \(\mathcal{L}_{m,n}\) and \(\mathcal{S}_{m+n}\). One such bijection is given by mapping a lattice path to the string that results by assigning each East step to 0 and each North step to 1 as we travel the path from \((0,0)\) to \((m,n)\). Using this construction, the lattice path in Figure 9.1 would get mapped to the binary string \(0101100\). Since no two lattice paths will map to the same string, our mapping is injective. Given a string in \(\mathcal{S}_{m+n}\), it is easy to find the lattice path in \(\mathcal{L}_{m,n}\) that maps to it, and so our function is also surjective. Thus, our mapping is a bijection between \(\mathcal{L}_{m,n}\) and \(\mathcal{S}_{m+n}\). We have shown that \(card(\mathcal{L}_{m,n})=card(\mathcal{S}_{m+n})\).

= [circle, draw, fill=black,inner sep=0pt, minimum size=.7mm]

When approaching Part (d) of the next problem, try creating a linear function \(f:(a,b)\to (c,d)\). Drawing a picture should help.

Problem 9.6. Prove each of the following. In each case, you should create a bijection between the two sets. Briefly justify that your functions are in fact bijections.

Figure 9.1: A North-East lattice path from (0,0) to (4,3).

1. \(card(\{a,b,c\})=card(\{x,y,z\})\)
2. \(card(\mathbb{N})=card(\{2n+1\mid n\in \mathbb{N}\})\)
3. \(card(\mathbb{N})=card(\mathbb{Z})\)
4. \(card((a,b))=card((c,d))\) (where \((a,b)\) and \((c,d)\) are intervals)
5. \(card(\mathbb{N})=card(\{\frac{1}{2^n}\mid n\in \mathbb{N}\})\)

Problem 9.7. If \(A\) is a set, do \(A\) and \(A\times \{x\}\) have the same cardinality? Justify your answer.

Problem 9.8. Let \(\mathcal{D}_n\) denote the collection of North-East lattice paths from \((0,0)\) to \((n,n)\) that never drop below the line \(y=x\). These types of lattice paths are often called Dyck paths after the German mathematician Walther Franz Anton von Dyck (1856–1934). A sequence of parentheses is balanced if it can be parsed syntactically. In other words, there should be the same number of open parentheses “(" and closed parentheses “)", and when reading from left to right there should never be more closed parentheses than open. For example, \(()()()\) and \(()(())\) are balanced parenthesizations consisting of three pairs of parentheses while \(())(()\) and \(()(()(\) are not balanced. Let \(\mathcal{B}_n\) denote the collection of balanced parenthesizations consisting of \(n\) pairs of parentheses. For example, \(\mathcal{B}_3=\{()()(), ()(()), (()()), (())(), ((()))\}\).

1. Find all Dyck paths in \(\mathcal{D}_3\).
2. Prove that \(card(\mathcal{D}_n)=card(\mathcal{B}_n)\).

For Part (b) of the next problem, start by defining \(\varphi:\mathcal{F}\to \mathcal{P}(\mathbb{N})\) so that \(\varphi(f)\) yields a subset of \(\mathbb{N}\) determined by when \(f\) outputs a 1.

Problem 9.9. Let \(\mathcal{F}\) denote the set of functions from \(\mathbb{N}\) to \(\{0,1\}\).

1. Describe at least three functions in \(\mathcal{F}\).
2. Prove that \(\mathcal{F}\) and \(\mathcal{P}(\mathbb{N})\) have the same cardinality.

Our first theorem concerning cardinality will likely not come as a surprise.

Theorem 9.10. Let \(A\), \(B\), and \(C\) be sets.

1. \(card(A)=card(A)\).
2. If \(card(A)=card(B)\), then \(card(B)=card(A)\).
3. If \(card(A)=card(B)\) and \(card(B)=card(C)\), then \(card(A)=card(C)\).

In light of the previous theorem, the next result should not be surprising.

Corollary 9.11. If \(X\) is a set, then “has the same cardinality as" is an equivalence relation on \(\mathcal{P}(X)\).

Theorem 9.12. Let \(A\), \(B\), \(C\), and \(D\) be sets such that \(card(A)=card(C)\) and \(card(B)=card(D)\).

1. If \(A\) and \(B\) are disjoint and \(C\) and \(D\) are disjoint, then \(card(A\cup B)=card(C\cup D)\).
2. \(card(A\times B)=card(C\times D)\).

Given two finite sets, it makes sense to say that one set is “larger than" another provided one set contains more elements than the other. We would like to generalize this idea to handle both finite and infinite sets.

Definition 9.13. Let \(A\) and \(B\) be sets. If there is an injective function from \(A\) to \(B\), then we say that the cardinality of \(A\) is less than or equal to the cardinality of \(B\). In this case, we write \(card(A)\leq card(B)\).

Theorem 9.14. Let \(A\), \(B\), and \(C\) be sets.

1. If \(A\subseteq B\), then \(card(A)\leq card(B)\).
2. If \(card(A)\leq card(B)\) and \(card(B)\leq card(C)\), then \(card(A)\leq card(C)\).
3. If \(C\subseteq A\) while \(card(B)=card(C)\), then \(card(B)\leq card(A)\).

It might be tempting to think that the existence of injective function from a set \(A\) to a set \(B\) that is not surjective would verify that \(card(A)\leq card(B)\) and \(card(A)\neq card(B)\). While this is true for finite sets, it is not true for infinite sets as the next problem asks you to verify.

Problem 9.15. Provide an example of sets \(A\) and \(B\) such that \(card(A)=card(B)\) despite the fact that there exists an injective function from \(A\) to \(B\) that is not surjective.

Definition 9.16. Let \(A\) and \(B\) be sets. We write \(card(A)< card(B)\) if \(card(A)\leq card(B)\) and \(card(A)\neq card(B)\).

As a reminder, the statements \(card(A)= card(B)\) and \(card(A)\leq card(B)\) are symbolic ways of asserting the existence of certain types of functions from \(A\) to \(B\). When we write \(card(A)<card(B)\), we are saying something much stronger than “There exists a function \(f:A\to B\) that is injective but not surjective." The statement \(card(A)<card(B)\) is asserting that every injective function from \(A\) to \(B\) is not surjective. In general, it is difficult to prove statements like \(card(A)\neq card(B)\) or \(card(A)<card(B)\).