Appendix D: List of Symbols
- Page ID
- 7094
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
| Symbol | Meaning |
| \(\to\) | Conditional statement |
| \(\mathbb{R}\) | set of real numbers |
| \(\mathbb{Q}\) | set of rational numbers |
| \(\mathbb{Z}\) | set of integers |
| \(\mathbb{N}\) | set of natural numbers |
| \(y \in A\) | \(y\) is an element of \(A\) |
| \(z \notin A\) | \(z\) is not an element of \(A\) |
| { | } | set builder notation |
| \(\forall\) | universal quantifier |
| \(\exists\) | existential quantifier |
| \(\emptyset\) | the empty set |
| \(\wedge\) | conjunction |
| \(vee\) | disjunction |
| \(\urcorner\) | negation |
| \(\leftrightarrow\) | biconditional statement |
| \(\equiv\) | logically equivalent |
| \(m\ |\ n\) | \(m\) divides \(n\) |
| \(a \equiv b\) (mod \(n\)) | \(a\) is congruent to \(b\) modulo \(n\) |
| \(|x|\) | the absolute value of \(x\) |
| \(A = B\) | \(A\) equals \(B\) (set equality) |
| \(A \subseteq B\) | \(A\) is a subset of \(B\) |
| \(A \not\subseteq B\) | \(A\) is not a subset of \(B\) |
| \(A \subset B\) | \(A\) is a proper subset of \(B\) |
| \(\mathcal{P}(A)\) | power set of \(A\) |
| \(|A|\) | cardinality of a finite set \(A\) |
| \(A \cap B\) | intersection of \(A\) and \(B\) |
| \(A^{c}\) | complement of \(A\) |
| \(A - B\) | set difference of \(A\) and \(B\) |
| \(A \times B\) | Cartesian product of \(A\) and \(B\) |
| \((a, b)\) | ordered pair |
| \(\mathbb{R} \times \mathbb{R}\) | Cartesian plane |
| \(\mathbb{R}^2\) | Cartesian plane |
| \(\bigcup_{X \in \mathcal{C} X\) | union of a family of sets |
| \(\bigcap_{X \in \mathcal{C} X\) | intersection of a finite family of sets |
| \(\bigcup_{j = 1}^{n} A_j\) | union of a finite family of sets |
| \(\bigcap_{j = 1}^{n} A_j\) | intersection of a finite family of sets |
| \(\bigcup_{j = 1}^{\infty} B_j\) | union of an infinite family of sets |
| \(\bigcap_{j = 1}^{\infty} B_j\) | intersection of a infinite family of sets |
| \(\{A_{\alpha}\ |\ \alpha \in \Lambda\}\) | indexed family of sets |
| \(\bigcup_{\alpha \in \Lambda} A_{\alpha}\) | union of an indexed family of sets |
| \(\bigcap_{\alpha \in \Lambda} A_{\alpha}\) | intersection of an indexed family of sets |
| \(n!\) | \(n\) factorial |
| \(f_1, f_2, f_3, ...\) | Fibonacci numbers |
| \(s(n)\) | sum of the divisors of \(n\) |
| \(f: A \to B\) | function from \(A\) to \(B\) |
| dom(\(f\)) | domain of the function \(f\) |
| codom(\(f\)) | codmain of the function \(f\) |
| \(f(x)\) | inage of \(x\) under \(f\) |
| range(\(f\)) | range of the function \(f\) |
| \(d(n)\) | number of divisors of \(n\) |
| \(I_{A}\) | identity function on the set \(A\) |
| \(p_1, p_2\) | projection functions |
| det\((A)\) | determinant of \(A\) |
| \(A^{T}\) | transpose of \(A\) |
| det: \(M_{2, 2} \to \mathbb{R}\) | determinant function |
| \(g \circ f: A \to C\) | composition of function \(f\) and \(g\) |
| \(f^{-1}\) | the inverse of the function \(f\) |
| Sin | the restricted sine function |
| Sin\(^{-1}\) | the inverse sine function |
| dom(\(R\)) | domain of the relation \(R\) |
| range(\(R\)) | range of the relation \(R\) |
| \(x\ R\ y\) | \(x\) is related to \(y\) |
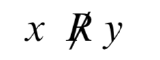 |
\(x\) is not related to \(y\) |
| \(x \sim y\) | \(x\) is related to \(y\) |
| \(x \nsim y\) | \(x\) is not related to \(y\) |
| \(R^{-1}\) | the inverse of the relation \(R\) |
| \([a]\) | equivalence class of \(a\) |
| \([a]\) | congruence class of \(a\) |
| \(\mathbb{Z}_{n}\) | the integers modulo \(n\) |
| \([a] \oplus [c]\) | addition in \(\mathbb{Z}_{n}\) |
| \([a] \odot [c]\) | multiplication in \(\mathbb{Z}_{n}\) |
| gcd(\(a\), \(b\)) | greatest common divisor of \(a\) and \(b\) |
| \(f(A)\) | image of \(A\) under the function \(f\) |
| \(f^{-1}(C)\) | pre-image of \(C\) under the funtion \(f\) |
| \(A \thickapprox B\) | \(A\) is equivalent to \(B\) \(A\) and \(B\) have the same cardinality |
| \(\mathbb{N}_{k}\) | \(\mathbb{N}_{k} = \{1, 2, ..., k\}\) |
| card\((A) = k\) | cardinality of \(A\) is \(k\) |
| \(aleph_{0}\) | cardinality of \(\mathbb{N}\) |
| \(c\) | cardinal number of the continuum |


