Appendix B: Answers for the Progress Checks
- Page ID
- 7092
Section 1.1
Progress Check 1.2
- This proposition is false. A counterexample is \(a = 2\) and \(b = 1\). For these values, \((a + b)^2 = 9\) and \(a^2 + b^2 = 5\).
- This proposition is true, as we can see by using \(x = 3\) and \(y = 7\). We could also use \(x = -2\) and \(y = 9\). There are many other possible choices for \(x\) and \(y\).
- This proposition appears to be true. Anytime we use an example where \(x\) is an even integer, the number \(x^2\) is an even integer. However, we cannot claim that this is true based on examples since we cannot list all of the examples where \(x\) is an even integer.
- This proposition appears to be true. Anytime we use an example where \(x\) and \(y\) are both integers, the number \(x \cdot y\) is an odd integer. However, we cannot claim that this is true based on examples since we cannot list all of the examples where both x and y are odd integers.
Progress Check 1.4
- (a) This does not mean the conditional statement is false since when \(x = -3\), the hypothesis is false, and the only time a conditional statement is false is when the hypothesis is true and the conclusion is false.
(b) This does not mean the conditional statement is true since we have not checked all positive real numbers, only the one where \(x = 4\).
(c) All examples should indicate that the conditional statement is true. - The number (\(n2 - n + 41\)) will be a prime number for all examples of \(n\) that are less than 41. However, when \(n = 41\), we get
\[\begin{array} {rcl} {n^2 - n + 41} &= & {41^2 - 41 + 41} \\ {n^2 - n + 41} &= & {41^2} \end{array}\]
So in the case where \(n = 41\), the hypothesis is true (41 is a positive integer) and the conclusion is false (\(41^2\) is not prime). Therefore, 41 is a counterexample that shows the conditional statement is false. There are other counterexamples (such as \(n = 42\), \(n = 45\), and \(n = 50\)), but only one counterexample is needed to prove that the statement is false.
Progress Check 1.5
- We can conclude that this function is continuous at 0.
- We can make no conclusion about this function from the theorem.
- We can make no conclusion about this function from the theorem.
- We can conclude that this function is not differentiable at 0.
Progress Check 1.7
- The set of rational numbers is closed under addition since \(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd}\).
- The set of integers is not closed under division. For example, \(\dfrac{2}{3}\) is not an integer.
- The set of rational numbers is closed under subtraction since \(\dfrac{a}{b} - \dfrac{c}{d} = \dfrac{ad - bc}{bd}\).
Section 1.2
Progress Check 1.10
All examples should indicate the proposition is true. Following is a proof.
Proof. We assume that \(m\) is an odd integer and will prove that (\(3m^2 + 4m + 6\)). Since \(m\) is an odd integer, there exists an integer \(k\) such that \(m D= 2k + 1\). Substituting this into the expression (\(3m^2 + 4m + 6\)) and using algebra, we obtain
\(\begin{array} {rcl} {3m^2 + 4m + 6} &= & {3(2k + 1)^2 + 4(2k + 1) + 6} \\ {} &= & {(12k^2 + 12k + 3) + (8k + 4) + 6} \\ {} &= & {12k^2 + 20k + 13} \\ {} &= & {12k^2 + 20k + 12 + 1} \\ {} &= & {2(6k^2 + 10k + 6) + 1} \end{array}\)
Progress Check 1.11
Proof. We let \(m\) be a real number and assume that \(m\), \(m + 1\), and \(m + 2\) are the lengths of the three sides of a right triangle. We will use the Pythagorean Theorem to prove that \(m = 3\). Since the hypotenuse is the longest of the three sides, the Pythagorean Theorem implies that \(m^2 + (m + 1)^2 = (m + 2)^2\). We will now use algebra to rewrite both sides of this equation as follows:
\(\begin{array} {rcl} {m^2 + (m^2 + 2m + 1)} &= & {m^2 + 4m + 4} \\ {2m^2 + 2m + 1} &= & {m^2 + 4m + 4} \end{array}\)
The last equation is a quadratic equation. To solve for \(m\), we rewrite the equation in standard form and then factor the left side. This gives
\(\begin{array} {rcl} {m^2 - 2m - 3} &= & {0} \\ {(m - 3) (m + 1)} &= & {0} \end{array}\)
The two solutions of this equation are \(m = 3\) and \(m = -1\). However, since \(m\) is the length of a side of a right triangle, \(m\) must be positive and we conclude that \(m = 3\). This proves that if \(m\), \(m + 1\), and \(m + 2\) are the lengths of the three sides of a right triangle, then \(m = 3\).
Section 2.1
Progress Check 2.1
- Whenever a quadrilateral is a square, it is a rectangle, or a quadrilateral is a rectangle whenever it is a square.
- A quadrilateral is a square only if it is a rectangle.
- Being a rectangle is necessary for a quadrilateral to be a square.
- Being a square is sufficient for a quadrilateral to be a rectangle.
Progress Check 2.2
| \(P\) | \(Q\) | \(P \wedge \urcorner Q\) | \(\urcorner (P \wedge Q)\) | \(\urcorner P \wedge \urcorner Q\) | \(\urcorner P \vee \urcorner Q\) |
| T | T | F | F | F | F |
| T | F | T | T | F | T |
| F | T | F | T | F | T |
| F | F | F | T | T | T |
Statements (2) and (4) have the same truth table.
Progress Check 2.4
| \(P\) | \(\urcorner P\) | \(P \vee \urcorner P\) | \(P \wedge \urcorner P\) |
| T | F | T | F |
| F | T | T | F |
| \(P\) | \(Q\) | \(P \vee Q\) | \(P \to (P \vee Q)\) |
| T | T | T | T |
| T | F | T | T |
| F | T | T | T |
| F | F | F | T |
Section 2.2
Progress Check 2.7
- Starting with the suggested equivalency, we obtain
\[\begin{array} {rcl} {(P \wedge \urcorner Q) \to R} &\equiv & {\urcorner (P \wedge \urcorner Q) \vee R} \\ {} &\equiv & {(\urcorner P \vee \urcorner (\urcorner Q)) \vee R} \\ {} &\equiv & {\urcorner P \vee (Q \vee R)} \\ {} &\equiv & {P \to (Q \vee R)} \end{array}\] - For this, let \(P\) be,“3 is a factor of \(a \cdot b\),” let \(Q\) be, “is a factor of \(a\),” and let \(R\) be, “3 is a factor of \(b\).” Then the stated proposition is written in the form \(P \to (Q \vee R)\). Since this is logically equivalent to \((P \wedge \urcorner Q) \to R\), if we prove that
if 3 is a factor of \(a \cdot b\) and 3 is not a factor of \(a\), then 3 is a factor of \(b\), then we have proven the original proposition.
Section 2.3
Progress Check 2.9
- \(10 \in A\), \(22 \in A\), \(13 \notin A\), \(0 \in A\), \(-12 \notin A\)
- \(A = B, A \subseteq B, B \subseteq A, A \subseteq C, A \subseteq D, B \subseteq C, B \subseteq D\)
Progress Check 2.11
- (a) Two values of \(x\) for which \(P(x)\) is false are \(x = 3\) and \(x = -4\).
(b) The set of all \(x\) for which \(P(x)\) is true is the set {-2, -1, 0, 1, 2}. - (a) Two examples for which \(R(x, y, z)\) is false are: \(x = 1, y = 1, z = 1\) and \(x = 3\), \(y = -1\), \(z = 5\).
(b) Two examples for which \(R(x, y, z)\) is true are: \(x = 3, y = 4, z = 5\) and \(x = 5, y = 12, z = 13\).
Progress Check 2.13
- The truth set is the set of all real numbers whose square is less than or equal to 9. The truth set is \(\{x \in \mathbb{R}\ |\ x^2 \le 9\} = \{x \in \mathbb{R}\ |\ -3 \le x \le 3\}\).
- The truth set is the set of all integers whose square is less than or equal to 9. The truth set is {-3, -2, -1, 0, 1, 2, 3}.
- The truth sets in Parts (1) and (2) equal are not equal. One purpose of this progress check is to show that the truth set of a predicate depends on the predicate and on the universal set.
Progress Check 2.15
\(A = \{4n - 3\ |\ n \in \mathbb{N}\} = \{x \in \mathbb{N}\ |\ x = 4n - 3 \text{ for some natural number \(n\)}\}.\)
\(B = \{-2n\ |\ \text{\(n\) is a nonnegative integer\}.\)
\(C = \{(\sqrt{2})^{2m - 1}\ |\ m \in \mathbb{N}\} = \{(\sqrt{2})^n\ |\ \text{\(n\) is an odd natural number}\}.\)
\(D = \{3^n\ |\ \text{\(n\) is a nonnegative integer}\}.\)
Section 2.4
Progress Check 2.18
- \(\bullet\) For each real number \(a\), \(a + 0 = a\).
\(\bullet\) \((\exists a \in \mathbb{R}) (a + 0 \ne a).\)
\(\bullet\) There exists a real number \(a\) such that \(a + 0 \ne a\). - \(\bullet\) For each real number \(x\), sin (2\(x\)) = 2(sin \(x\))(cos \(x\)).
\(\bullet\) \((\exists x \in \mathbb{R})\) (sin (2\(x\)) \(\ne\) 2 (sin \(x\)) (cos \(x\))).
\(\bullet\) There exists a real number \(x\) such that sin (2\(x\)) \(\ne\) 2 (sin \(x\)) (cos \(x\)). - \(\bullet\) For each real number \(x\), \(\text{tan}^2 x + 1 = \text{sec}^2 x\).
\(\bullet\) \((\exists x \in \mathbb{R}) (\text{tan}^2 x + 1 \ne \text{sec}^2 x)\).
\(\bullet\) There exists a real number \(x\) such that \(\text{tan}^2 x + 1 \ne \text{sec}^2 x\). - \(\bullet\) There exists a rational number \(x\) such that \(x^2 - 3x - 7 = 0\).
\(\bullet\) \((\forall x \in \mathbb{Q})(x^2 - 3x - 7 \ne 0).\)
\(\bullet\) For each rational number \(x\), \(x^2 - 3x - 7 \ne 0\). - \(\bullet\) There exists a real number \(x\) such that \(x^2 + 1 = 0\).
\(\bullet\) \((\forall x \in \mathbb{R})(x^2 + 1 \ne 0).\)
\(\bullet\) For each real number \(x\), \(x^2 + 1 \ne 0\).
Progress Check 2.19
- A counterexample is \(n = 4\) since \(4^2 + 4 + 1 = 21\), and 21 is not prime.
- A counterexample is \(x = \dfrac{1}{4}\) since \(\dfrac{1}{4}\) is positive and \(2(\dfrac{1}{4})^2 = \dfrac{1}{8}\) and \(\dfrac{1}{8} \le \dfrac{1}{4}\).
Progress Check 2.20
1. An integer \(n\) is a multiple of 3 provided that \(\exists k \in \mathbb{Z})(n = 3k)\).
4. An integer \(n\) is not a multiple of 3 provided that \(\forall k \in \mathbb{Z})(n \ne 3k)\).
5. An integer \(n\) is not a multiple of 3 provided that for every integer \(k\), \(n \ne 3k\).
Progress Check 2.21
- \((\exists x \in \mathbb{Z})(\exists y \in \mathbb{Z}) (x + y \ne 0)\).
- There exist integers \(x\) and \(y\) such that \(x + y \ne 0\).
Section 3.1
Progress Check 3.2
- For each example in Part (1), the integer \(a\) divides the sum \(b + c\).
- Conjecture: For all integers \(a\), \(b\), and \(c\) with \(a \ne 0\), if \(a\) divides \(b\) and \(a\) divides \(c\), then \(a\) divides \(b + c\).
- A Know-show table for a proof of the conjecture in Part (3).
| Step | Know | Reason |
| \(P\) | \(a\ |\ b\) and \(a\ |\ c\) | Hypothesis |
| \(P\)1 | \((\exists s \in \mathbb{Z})(b = a \cdot s)\) \((\exists t \in \mathbb{Z})(c = a \cdot t)\) |
Definition of "divides" |
| \(P\)2 | \(b + c = as + at\) | Substituting for \(b\) and \(c\) |
| \(P\)3 | \(b + c = a(s + t)\) | Distributive property |
| \(Q\)1 | \(s + t\) is an integer | \(\mathbb{Z}\) is closed under addition |
| \(Q\) | \(a\ |\ (b + c)\) | Definition of "divides" |
| Step | Show | Reason |
Progress Check 3.3
A counterexample for this statement will be values of a and b for which 5 divides \(a\) or 5 divides \(b\), and 5 does not divide \(5a + b\). One counterexample for the statement is \(a = 5\) and \(b = 1\). For these values, the hypothesis is true since 5 divides a and the conclusion is false since \(5a + b = 26\) and 5 does not divide 26.
Progress Check 3.4
- Some integers that are congruent to 5 modulo 8 are -11, -3, 5, 13, and 21.
- \(\{x \in \mathbb{Z}\ |\ x \equiv 5\text{ (mod 8)\} = \{..., -19, -11, -3, 5, 13, 21, 29, ...\}\).
- For example, -3 + 5 = 2, -11 + 29 = 18, 13 + 21 = 34.
- If we subtract 2 from any of the sums obtained in Part (3), the result will be a multiple of 8. This means that the sum is congruent to 2 modulo 8. For example, \(2 - 2 = 0\), \(18 - 2 = 16\), \(34 - 2 = 32\).
Progress Check 3.6
- To prove that 8 divides \((a + b - 2)\), we can prove that there exists an integer \(q\) such that (\(a + b - 2 = 8q\)).
- Since 8 divides (\(a - 5\)) and (\(b - 5\)), there exist integers \(k\) and \(m\) such that \(a - 5 - 8k\) and \(b - 5 = 8m\).
- \(a = 5 + 8k\) and \(b = 5 + 8m\).
- \(a + b - 2 = (5 + 8k) + 5 + 8m) - 2 = 8 + 8k + 8m = 8(1 + k + m)\).
- Proof. Let a and b be integers and assume that \(a \equiv 5\) (mod 8) and \(b \equiv 5\) (mod 8). We will prove that \((a + b) \equiv 2\) (mod 8\). Since 8 divides \((a - 5)\) and \((b - 5)\), there exist integers \(k\) and \(m\) such that \(a - 5 = 8k\) and \(b - 5 = 8m\). We then see that
\[\begin{array} {a + b - 2} &= & {(5 + 8k) + (5 + 8m) - 2] \\ {} &= & {8 + 8k + 8m} \\ {} &= & {8(1 + k + m)} \end{array}\]
By the closure properties of the integers, \((1 + k + m)\) is an integer and so the last equation proves that 8 divides (\(a + b - 2\)) and hence, \((a + b) \equiv 2\) (mod 8). This proves that if \(a \equiv 5\) (mod 8) and \(b \equiv 5\) (mod 8), then \((a + b) \equiv 2\) (mod 8).
Section 3.2
Progress Check 3.8
- For all real numbers \(a\) and \(b\), if \(ab = 0\), then \(a = 0\) or \(b = 0\).
- For all real numbers \(a\) and \(b\), if \(ab = 0\) and \(a \ne 0\), \(b = 0\)
- This gives
\[\dfrac{1}{a}(ab) = \dfrac{1}{a} \cdot 0.\]
We now use the associative property on the left side of this equation and simplify both sides of the equation to obtain
\[\begin{array} {rcl} {(\dfrac{1}{a} \cdot a) b} &= & {0} \\ {1 \cdot b} &= & {0} \\ {b} &= & {0} \end{array}\]
Therefore, \(b = 0\) and this completes the proof of a statement that is logically equivalent to the contrapositive. Hence, we have proved the proposition.
Section 3.3
Progress Check 3.15
- There exists a real number \(x\) such that \(x\) is irrational and \(\sqrt[3]{x}\) is rational.
- There exists a real number \(x\) such that \(x + \sqrt{2}\) is rational and \((-x + \sqrt{2})\) is rational.
- There exist integers \(a\) and \(b\) such that 5 divides \(ab\) and 5 does not divide \(a\) and 5 does not divide \(b\).
- There exist real numbers \(a\) and \(b\) such that \(a > 0\) and \(b > 0\) and \(\dfrac{2}{a} + \dfrac{2}{b} = \dfrac{4}{a + b}\).
Progress Check 3.16
- Some integers that are congruent to 2 modulo 4 are -6. -2, 2, 6, 10, and some integers that are congruent to 3 modulo 6 are: -9, -3, 3, 9, 15. There are no integers that are in both of the lists.
- For this proposition, it is reasonable to try a proof by contradiction since the conclusion is stated as a negation.
- Proof. We will use a proof by contradiction. Let \(n \in \mathbb{Z}\) and assume that \(n \equiv 2\) (mod 4) and that \(n \equiv 3\) (mod 6). Since \(n \equiv 2\) (mod 4), we know that 4 divides \(n - 2\). Hence, there exists an integer \(k\) such that
\[n - 2 = 4k.\]We can also use the assumption that \(n \equiv 3\) (mod 6) to conclude that 6 divides \(n - 3\) and that there exists an integer \(m\) such that
\[n - 3 = 6m.\]
If we now solve equations (B.5) and (B.6) for n and set the two expressions equal to each other, we obtain
\[4k + 2 = 6m + 3.\]
However, this equation can be rewritten as
\[2(2k + 1) = 2(3m + 1) + 1.\]
Since \(2k + 1\) is an integer and \(3m + 1\) is an integer, this last equation is a contradiction since the left side is an even integer and the right side is an odd integer. Hence, we have proven that if \(n \equiv 2\) (mod 4), then \(n \equiv 3\) (mod 6).
Progress Check 3.18
- \(x^2 + y^2 = (2m + 1)^2 + (2n + 1)^2 = 2(2m^2 + 2m + 2n^2 + 2n + 1).\)
- Using algebra to rewrite the last equation, we obtain
\[4m^2 + 4m + 4n^2 + 4n + 2 = 4k^2.\]
If we divide both sides of this equation by 2, we see that \(2m^2 + 2m + 2n^2 + 2n + 1 = 2k^2\) or
\[2(m^2 + m + n^2 + n) + 1 = 2k^2.\]
However, the left side of the last equation is an odd integer and the right side is an even integer. This is a contradiction, and so we have proved that for all integers \(x\) and \(y\), if \(x\) and \(y\) are odd integers, then there does not exist an integer \(z\) such that \(x^2 + y^2 = z^2\).
Section 3.4
Progress Check 3.21
Proposition. For each integer \(n\), \(n^2 - 5n + 7\) is an odd integer.
Proof. Let \(n\) be an integer. We will prove that \(n^2 - 5n + 7\) is an odd integer by examining the case where \(n\) is even and the case where \(n\) is odd.
In the case where \(n\) is even, there exists an integer m such that \(n = 2m\). So in this case,
\(\begin{array} {rcl} {n^2 - 5n + 7} &= & {(2m^2) - 5(2m) + 7} \\ {} &= & {4m^2 - 10m + 6 + 1} \\ {} &= & {2(2m^2 - 5m + 3) + 1.} \end{array}\)
Since (\(2m^2 - 5m + 3\)) is an integer, the last equation shows that if \(n\) is even, then \(n^2 - 5n + 7\) is odd.
In the case where \(n\) is odd, there exists an integer \(m\) such that \(n = 2m + 1\). So in this case,
\(\begin{array} {rcl} {n^2 - 5n + 7} &= & {(2m + 1)^2 - 5(2m + 1) + 7} \\ {} &= & {4m^2 - 14m + 3} \\ {} &= & {2(2m^2 - 7m + 1) + 1.} \end{array}\)
Since (\(2m^2 - 7m + 1\)) is an integer, the last equation shows that if \(n\) is odd, then \(n^2 - 5n + 7\) is odd. Hence, by using these two cases, we have shown that for each integer \(n\), \(n^2 - 5n + 7\) is an odd integer.
Progress Check 3.24
- |4.3| = 4.3 and |-\(\pi\)| = \(\pi\)
- (a) \(t = 12\) or \(t = -12\)
(b) \(t + 3 = 5\) or \(t + 3 = -5\). So \(t = 2\) or \(t = -8\).
(c) \(t - 4 = \dfrac{1}{5}\) or \(t - 4 = -\dfrac{1}{5}\). So \(t = \dfrac{21}{5}\) or \(t = \dfrac{19}{5}\).
(d) \(3t - 4 = 8\) or \(3t - 4 = -8\). So \(t = 4\) or \(t = -\dfrac{4}{3}\).
Section 3.5
Progress Check 3.26
- (a) The possible remainders are 0, 1, 2, and 3.
(b) The possible remainders are 0, 1, 2, 3, 4, 5, 6, 7, and 8.
(a) \(17 = 5 \cdot 3 + 2\)
(b) \(-17 = (-6) \cdot 3 + 1\)
(c) \(73 = 10 \cdot 7 + 3\)
(d) \(-73 = (-11) \cdot 7 + 4\)
(e) \(436 = 16 \cdot 27 + 4\)
(f) \(539 = 4 \cdot 110 + 99\)
Progress Check 3.29
Proof. Let \(n\) be a natural number and let \(a, b, c\) and \(d\) be integers.We assume that \(a \equiv b\) (mod \(n\)) and \(c \equiv d\) (mod \(n\)) and will prove that \((a + c) \equiv (b + d)\) (mod \(n\)). Since \(a \equiv b\) (mod \(n\)) and \(c \equiv d\) (mod \(n\)), \(n\) divides \(a - b\) and \(c - d\) and so there exist integers \(k\) and \(q\) such that \(a - b = nk\) and \(c - d = nq\). We can then write \(a = b + nk\) and \(c = d + nq\) and obtain
\(\begin{array} {rcl} {a + c} &= & {(b + nk) + (d + nq)} \\ {} &= & {(b + d) + n(k + q)} \end{array}.\)
By subtracting \((b + d)\) from both sides of the last equation, we see that
\((a + c) - (b + d) = n(k + q).\)
Since \((k + q)\) is an integer, this proves that \(n\) divides \((a + c) - (b + d)\), and hence, we can conclude that \((a + c) \equiv (b + d)\) (mod \(n\)).
Progress Check 3.34
Case 2. (\(a \equiv 2\) (mod 5)). In this case, we use Theorem 3.28 to conclude that
\(a^2 \equiv 2^2\) (mod 5) or \(a^2 \equiv 4\) (mod 5).
This proves that if \(a \equiv 2\) (mod 5), then \(a^2 \equiv 4\) (mod 5).
Case 3. (\(a \equiv 3\) (mod 5)). In this case, we use Theorem 3.28 to conclude that
\(a^2 \equiv 3^2\) (mod 5) or \(a^2 \equiv 9\) (mod 5).
We also know that \(9 \equiv 4\) (mod 5). So we have \(a^2 \equiv 9\) (mod 5) and \(9 \equiv 4\) (mod 5), and we can now use the transitive property of congruence (Theorem 3.30) to conclude that \(a^2 \equiv 4\) (mod 5). This proves that if \(a \equiv 3\) (mod 5), then \(a^2 \equiv 4\) (mod 5).
Section 4.1
Progress Check 4.1
- It is not possible to tell if \(1 \in T\) and \(5 \in T\).
- True.
- True. The contrapositive is, "If \(2 \in T\), then \(5 \in T\)," which is true.
- True.
- False. If \(k \in T\), then \(k + 1 \in T\).
- True, since "k \notin t\) OR \(k + 1 \in T\)" is logically equivalent to "If \(k \in T\), then \(k + 1 \in T\)."
- It is not possible to tell if this is true. It is the converse of the conditional statement, “For each integer \(k\), if \(k \in T\), then \(k + 1 \in T\)."
- True. This is the contrapositive of the conditional statement, “For each integer \(k\), if \(k \in T\), then \(k + 1 \in T\)."
Progress Check 4.3
Proof. Let \(P(n)\) be the predicate, "\(1 + 2 + 3 + \cdot\cdot\cdot + n = \dfrac{n(n + 1)}{2}\)." For basis step, notice that the equation \(1 = \dfrac{1(1 + 1)}{2}\) shows that \(P(1)\) is true. Now let \(k\) be a natural number an assume that \(P(k)\) is true. That is, assume that
\[1 + 2 + 3 + \cdot\cdot\cdot + k = \dfrac{k(k + 1)}{2}.\]
We now need to prove that \(P(k + 1)\) is true or that
\[1 + 2 + 3 + \cdot\cdot\cdot + k + (k + 1) = \dfrac{(k + 1)(k + 2)}{2}.\]
By adding \((k + 1)\) to both sides of equation (B.11), we see that
\(\begin{array} {rcl} {1 + 2 + 3 + \cdot\cdot\cdot + k + (k + 1)} &= & {\dfrac{k(k + 1)}{2} + (k + 1)} \\ {} &= & {\dfrac{k(k + 1) + 2(k + 1)}{2}} \\ {} &= & {\dfrac{k^2 + 3k + 2}{2}} \\ {} &= & {\dfrac{(k + 1)(k + 2)}{2}.} \end{array}\)
By comparing the last equation to equation (2), we see that we have proved that if \(P(k)\) is true, then \(P(k + 1)\) is true, and the inductive step has been established. Hence, by the Principle of Mathematical Induction, we have proved that for each integer \(n\), \(1 + 2 + 3 + \cdot\cdot\cdot + n = \dfrac{n(n + 1)}{2}\).
Progress Check 4.5
For the inductive step, let \(k\) be a natural number and assume that \(P(k)\) is true. That is, assume that \(5^k \equiv 1\) (mod 4).
- To prove that \(P(k + 1)\) is true, we must prove \(5^{k + 1} \equiv 1\) (mod 4).
- Since \(5^{k + 1} = 5 \cdot 5^{k}\), we multiply both sides of the congruence \(5^{k} \equiv 1\) (mod 4) by 5 and obtain
\[5 \cdot 5^k \equiv 5 \cdot 1 \text{ (mod 4) or}\ \ \ \ \ \ \ \ 5^{k + 1} \equiv 5 \text{ (mod 4).}\] - Since \(5^{k + 1} \equiv 5\) (mod 4) and we know that \(5 \equiv 1\) (mod 4), we can use the transitive property of congruence to obtain \(5^{k + 1} \equiv 1\) (mod 4). This proves that if \(P(k)\) is true, then \(P(k + 1)\) is true, and hence, by the Principle of Mathematical Induction, we have proved that for each natural number \(n\), \(5^n \equiv 1\) (mod 4).
Section 4.2
Progress Check 4.8
- For each natural number \(n\), if \(n \ge 3\), then \(3^n > 1 + 2^n\).
- For each natural number \(n\), if \(n \ge 6\), then \(2^n > (n + 1)^2\).
- For each natural number \(n\), if \(n \ge 6\), then \((1 + \dfrac{1}{n})^n > 2.5\).
Progress Check 4.10
Construct the following table and use it to answer the first two questions. The table shows that \(P(3)\), \(P(5)\), and \(P(6)\) are true. We can also see that \(P(2)\), \(P(4)\), and \(P(7)\) are false. It also appears that if \(n \in \mathbb{N}\) and \(n \ge 8\), then \(P(n)\) is true.
| \(x\) | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 0 | 1 | 1 |
| \(y\) | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 |
| \(3x+ 5y\) | 0 | 3 | 6 | 9 | 12 | 5 | 8 | 11 | 10 | 13 | 18 |
The following proposition provides answers for Problems (3) and (4).
Proposition 4.11. For all natural numbers \(n\) with \(n \ge 8\), there exist non-negative integers \(x\) and \(y\) such that \(n = 3x + 5y\).
Proof. (by mathematical induction) Let \(\mathbb{Z}^{\ast} = \{x \in \mathbb{Z}\ |\ x \ge 0\}\), and for each natural number \(n\), let \(P(n)\) be, "there exist \(x, y \in \mathbb{Z}^{\ast}\) such that \(n = 3x + 5y\)."
Basis Step: Using the table above, we see that \(P(8)\), \(P(9)\), and \(P(10)\) are true.
Inductive Step: Let \(k \in \mathbb{N}\) with \(k \ge 13\). assume that \(P(8)\), \(P(9)\), ..., \(P(k)\) are true. Now, notice that
\(k + 1 = 3 + (k - 2).\)
Since \(k \ge 10\), we can conclude that \(k - 2 \ge 8\) and hence \(P(k - 2)\) is true. Therefore, there exist non-negative integers \(u\) and \(v\) such that \(k - 2 = (3u + 5v)\). Using this equation, we see that
\(\begin{array} {k + 1} &= & {3 + (3u + 5v)} \\ {} &= & {3(1 + u) + 5v}. \end{array}\)
Hence, we can conclude that \(P(k + 1)\) is true. This proves that if \(P(8)\), \(P(9)\), ..., \(P(k)\) are true, then \(P(k + 1)\) is true. Hence, by the Second Principle of Mathematical Induction, for all natural numbers \(n\) with \(n \ge 8\), there exist nonnegative integers \(x\) and \(y\) such that \(n = 3x + 5y\).
Section 4.3
Progress Check 4.12
Proof. We will use a proof by induction. For each natural number \(n\), we let \(P(n)\) be,
\(f_{3n}\) is an even natural number.
Since \(f_3 = 2\), we see that \(P(1)\) is true and this proves the basis step.
For the inductive step, we let \(k\) be a natural number and assume that \(P(k)\) is true. That is, assume that \(f_{3k}\) is an even natural number. This means that there exists an integer m such that
\[f_{3k} = 2m.\]
We need to prove that \(P(k + 1)\) is true or that \(f_{3(k + 1)}\) is even. Notice that \(3(k + 1) = 3k + 3\) and, hence, \(f_{3(k + 1) = f_{3k + 3}\). We can now use the recursion formula for the Fibonacci numbers to conclude that
\(f_{3k + 3} = f_{3k + 2} + f_{3k + 1}\).
Using the recursion formula again, we get \(f_{3k + 2} = f_{3k + 1} + f_{3k}\). Putting this all together, we see that
\[\begin{array} {rcl} {f_{3(k + 1)}} &= & {f_{3k + 3}} \\ {} &= & {f_{3k + 2} +f_{3k + 1}} \\ {} &= & {(f_{3k + 1} + f_{3k}) + f_{3k + 1}} \\ {} &= & {2f_{3k + 1} + f_{3k}.} \end{array}\]
We now substitute the expression for \(f_{3k}\) in equation (B.14) into equation (B.15). This gives
\[\begin{array} {rcl} {f_{3(k + 1)}} &= & {2f_{3k + 1} + 2m} \\ {f_{3(k + 1)}} &= & {2(f_{3k + 1} + m)} \end{array}\]
This preceding equation shows that \(f_{3(k + 1)}\) is even. Hence it has been proved that if \(P(k)\) is true, then \(P(k + 1)\) is true and the inductive step has been established. By the Principle of Mathematical Induction, this proves that for each natural number \(n\), the Fibonacci number \(f_{3n}\) is an even natural number.
Section 5.1
Progress Check 5.3

Progress Check 5.4
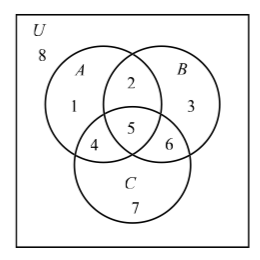
Using the standard Venn diagram for three sets shown above:
(a) For the set \((A \cap B) \cap C\), region 5 is shaded.
(b) For the set \((A \cap B) \cup C\), the regions 2, 4, 5, 6, 7 are shaded.
(c) For the set \((A^{c} \cup B)\), the regions 2, 3, 5, 6, 7, 8 are shaded.
(d) For the set \((A^{c} \cap (B \cup C))\), the regions 3, 6, 7 are shaded.
Section 5.2
Progress Check 5.8
\(A = \{x \in \mathbb{Z}\ |\ x \text{ is multiple of 9}\}\) and \(B = \{x \in \mathbb{Z}\ |\ x \text{ is a multiple of 3}\}.\)
- The set \(A\) is a subset of \(B\). To prove this, we let \(x \in A\). Then there exists an integer \(m\) such that \(x = 9m\), which can be written as
\[x = 3(3m).\]
Since \(3m \in \mathbb{Z}\), the last equation proves that \(x\) is a multiple of 3 and so \(x \in B\). Therefore, \(A \subseteq B\). - The set \(A\) is not equal to the set \(B\). We note that \(3 \in B\) but \(3 \notin A\). Therefore, \(B \not\subseteq A\) and, hence, \(A \ne B\).
Progress Check 5.9
| Step | Know | Reason |
| \(P\) | \(A \subseteq B\) | Hypothesis |
| \(P\)1 | Let \(x \in B^{c}\). | Choose an arbitrary element of \(B^{c}\). |
| \(P\)2 | If \(x \in A\), then \(x \in B\). | Definition of "subset" |
| \(P\)3 | If \(x \notin B\), then \(x \notin A\). | Contrapositive |
| \(P\)4 | If \(x \in B^{c}\), then \(x \in A^{c}\). | Step \(P\)3 and definition of “complement” |
| \(Q\)2 | The element \(x\) is in \(A^{c}\). | Step \(P\)1 and \(P\)4 |
| \(Q\)1 | Every element of \(B^{c}\) is an element of \(A^{c}\). | The choose-an-element method with Steps \(P\)1 and \(Q\)2. |
| \(Q\) | \(B^{c} \subseteq A^{c}\) | Definition of "subset" |
Progress Check 5.12
Proof. Let \(A\) and \(B\) be subsets of some universal set. We will prove that \(A - B = A \cap B^{c}\) by proving that each set is a subset of the other set. We will first prove that \(A - B \subseteq A \cap B^{c}\). Let \(x \in A - B\). We then know that \(x \in A\) and \(x \notin B\). However, \(x \notin B\) implies that \(x \in B^c\). Hence, \(x \in A\) and \(x \in B^{c}\), which means that \(x \in A \cap B^{c}\). This proves that \(A - B \subseteq A \cap B^{c}\).
To prove that \(A \cap B^{c} \subseteq A - B\), we let \(y \in A \cap B^{c}\). This means that \(y \in A\) and \(y \in B^{c}\), and hence, \(y \in A\) and \(y \notin B\). Therefore, \(y \in A - B\) and this proves that \(A \cap B^{c} \subseteq A - B\). Since we have proved that each set is a subset of the other set, we have proved that \(A - B = A \cap B^{c}\).
Progress Check 5.15
Proof. Let \(A = \{x \in \mathbb{Z}\ |\ x \equiv 3 \text{ (mod 12)}\}\) and \(B = \{y \in \mathbb{Z}\ |\ y \equiv 2 \text{ (mod 8)}\}\). We will use a proof by contradiction to prove that \(A \cap B = \emptyset\). So we assume that \(A \cap B \ne \emptyset\) and let \(x \in A \cap B\). We can then conclude that \(x \equiv 3 \text{ (mod 12)}\) and that \(x \equiv 2\) (mod 8). This means that there exist integers \(m\) and \(n\) such that
\(x = 3 + 12m\) and \(x = 2 + 8n\).
By equating these two expressions for \(x\), we obtain \(3 + 12m = 2 + 8n\), and this equation can be rewritten as \(1 = 8n - 12m\). This is a contradiction since 1 is an odd integer and \(8n - 12m\) is an even integer. We have therefore proved that \(A \cap B = \emptyset\).
Section 5.3
Progress Check 5.19
- In our standard configuration for a Venn diagram with three sets, regions 1, 2, 4, 5, and 6 are the shaded regions for both \(A \cup (B \cap C)\) and \((A \cup B) \cap (A \cup C)\).
- Based on the Venn diagrams in Part (1), it appears that \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\).
Progress Check 5.21
- Using our standard configuration for a Venn diagram with three sets, regions 1, 2, and 3 are the regions that are shaded for both \((A \cup B) - C\) and \((A - C) \cup (B- C)\).
- \(\begin{array} {rclcr} {(A \cup B) - C} &= & {(A \cup B) \cap C^{c}} & & {\text{(Theorem 5.20)}} \\ {} &= & {C^{c} \cap (A \cup B)} & & {\text{(Commutative Property)}} \\ {} &= & {(C^{c} \cap A) \cup (C^{c} \cap B)} & & {\text{(Distributive Property)}} \\ {} &= & {(A \cap C^{c}) \cup (B \cap C^{c})} & & {\text{(Commutative Property)}} \\ {} &= & {(A - C) \cup (B - C)} & & {\text{(Theorem 5.20)}} \end{array}\)
Section 5.4
Progress Check 5.23
- Let \(A = \{1, 2, 3\}\), \(T = \{1, 2\}\), \(B = \{a, b\}\), and \(C = \{a, c\}\).
(a) \(A \times B = \{(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)\}\)
(b) \(T \times B = \{(1, a), (1, b), (2, a), (2, b)\}\)
(c) \(A \times C = \{(1, a), (1, c), (2, a), (2, c), (3, a), (3, c)\}\)
(d) \(A \times (B \cap C) = \{(1, a), (2, a), (3, a)\}\)
(e) \((A \times B) \cap (A \times C) = \{(1, a), (2, a), (3, a)\}\)
(f) \(A \times (B \cup C) = \{(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)\}\)
(g) \((A \times B) \cup (A \times C) = \{(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)\}\)
(h) \(A \times (B - C) = \{(1, b), (2, b), (3, b)\}\)
(i) \((A \times B) - (A \times C) = \{(1, b), (2, b), (3, b)\}\)
(j) \(B \times A = \{(a, 1), (b, 1), (a, 2), (b, 2), (a, 3), (b, 3)\}\) - \(\begin{array} {lcl} {T \times B \subseteq A \times B} & & {A \times (B \cup C) = (A \times B) \cup (A \times C)} \\ {A \times (B \cap C) = (A \times B) \cap (A \times C)} & & {A \times (B - C) = (A \times B) - (A \times C)} \end{array}\)
Progress Check 5.24
- (a) \(A \times B = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y < 4\}\)
(b) \(T \times B = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 1 < x < 2 \text{ and } 2 \le y < 4\}\)
(c) \(A \times C = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 3 < y \le 6\}\)
(d) \(A \times (B \cap C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 3 < y < 4\}\)
(e) \((A \times B) \cap (A \times C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 3 < y < 4\}\)
(f) \(A \times (B \cup C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 5\}\)
(g) \((A \times B) \cup (A \times C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 5\}\)
(h) \(A \times (B - C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 3\}\)
(i) \((A \times B) - (A \times C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 3\}\)
(j) \(B \times A = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 2 \le x <4 \text{ and } 0 \le y \le 2\}\) - \(T \times B \subseteq A \times B\)
\(A \times (B \cap C) = (A \times C) \cap (A \times C)\)
\(A \times (B \cup C) = (A \times C) \cup (A \times C)\)
\(A \times (B - C) = (A \times C) - (A \times C)\)
Section 5.5
Progress Check 5.26
- \(\bigcup_{j = 1}^{6} A_j = \{1, 2, 3, 4, 5, 6, 9, 16, 25, 36\}\)
- \(\bigcap_{j = 1}^{6} A_j = \{1\}\)
- \(\bigcup_{j = 3}^{6} A_j = \{3, 4, 5, 6, 9, 16, 25, 36\}\)
- \(\bigcap_{j = 3}^{6} A_j = \{1\}\)
- \(\bigcup_{j = 1}^{\infty} A_j = \mathbb{N}\)
- \(\bigcap_{j = 1}^{\infty} A_j = \{1\}\)
Progress Check 5.27
- \(A_{1} = \{7, 14\}\), \(A_{2} = \{10, 12\}\), \(A_{3} = \{10, 12\}\), \(A_{4} = \{8, 14\}\).
- The statement is false. For example, \(2 \ne 3\) and \(A_2 = A_3\).
- The statement is false. For example, \(1 \ne -1\) and \(B_1 = B_{-1}\).
Progress Check 5.29
- Since \(\bigcup_{\alpha \in \mathbb{R}^{+}} A_{\alpha} = (-1, \infty)\), \((\bigcup_{\alpha \in \mathbb{R}^{+}} A_{\alpha})^{c} = (-\infty, 1]\).
- \(\bigcap_{\alpha \in \mathbb{R}^{+}} A_{\alpha}^{c} = (-\infty, -1]\).
- Since \(\bigcap_{\alpha \in \mathbb{R}^{+}} A_{\alpha} = (-1, 0]\), \((\bigcap_{\alpha \in \mathbb{R}^{+}} A_{\alpha})^{c} = (-\infty, 1] \cup (0, \infty)\).
- \(\bigcup_{\alpha \in \mathbb{R}^{+}} A_{\alpha}^{c} = (-\infty, -1] \cup (0, \infty)\).
Progress Check 5.32
All three families of sets (\(\mathcal{A}\), \(\mathcal{B}\), and \(\mathcal{C}\) are disjoint families of sets. One the family \(\mathcal{A}\) is a pairwise disjoint family of sets.
Section 6.1
Progress Check 6.1
- \(f(-3) = 24\)
\(f(\sqrt{8}) = 8 - 5\sqrt{8}\) - \(g(2) = -6, g(-2) = 14\)
- {-1, 6}
- {-1, 6}
- \(\{\dfrac{5 + \sqrt{33}}{2}, \dfrac{5 - \sqrt{33}}{2}\}\)
- \(\emptyset\)
Progress Check 6.2
- (a) The domain of the function \(f\) is the set of all people.
(b) A codomain for the function \(f\) is the set of all days in a leap year.
(c) This means that the range of the function \(f\) is equal to its codomain. - (a) The domain of the function \(s\) is the set of natural numbers.
(b) A codomain for the function \(s\) is the set of natural numbers.
(c) This means that the range of \(s\) is not equal to the set o natural numbers.
Progress Check 6.3
- \(f(-1) \thickapprox -3\) and \(f(2) \thickapprox -2.5\).
- Values of \(x\) for which \(f(x) = 2\) are approximately -2.8, -1.9, 0.3, 1.2, and 3.5.
- The range of \(f\) appears to be the closed interval [-3.2, 3.2] or \(\{y \in \mathbb{R}\ |\ -3.2 \le y \le 3.2\}\).
Progress Check 6.4
Only the arrow diagram in Figure (a) can be used to represent a function from \(A\) to \(B\). The range of this function is the set \(\{a, b\}\).
Section 6.2
Progress Check 6.5
- \(f(0) = 0\), \(f(1) = 1\), \(f(2) = 1\), \(f(3) = 1\), \(f(4) = 1\).
- \(g(0) = 0\), \(g(1) = 1\), \(g(2) = 2\), \(g(3) = 3\), \(g(4) = 4\).
Progress Check 6.6
\(I_{\mathbb{Z}_5} \ne f\) and \(I_{\mathbb{Z}_5} = g\)
Progress Check 6.7
- 3.5
- 4.02
- \(\dfrac{\pi + \sqrt{2}{4}\)
- The process of finding the average of a finite set of real numbers can be thought of as a function from \(\mathcal{F}(\mathbb{R})\) to \(\mathbb{R}\). So the domain is \(\mathcal{F}(\mathbb{R})\), the codomain is \(\mathbb{R}\), and we can define a function avg: \(\mathcal{F}(\mathbb{R}) \to \mathbb{R}\) as follows: If \(A \in \mathcal{F}(\mathbb{R})\) and \(A = \{a_1, a_2, ..., a_n\}\), then ave\((A) = \dfrac{a_1 + a_2 + \cdot\cdot\cdot a_n}{n}\).
Progress Check 6.8
- The sixth terms is \(\dfrac{1}{18}\) and the tenth term is \(\dfrac{1}{30}\).
- The sixth terms is \(\dfrac{1}{36}\) and the tenth term is \(\dfrac{1}{100}\).
- The sixth terms is 1 and the tenth term is 1.
Progress Check 6.9
- \(g(0, 3) = -3\); \(g(3, -2) = 11\); \(g(-3, -2) = 11\); \(g(7, -1) = 50\).
- \(\{(m, n) \in \mathbb{Z} \times \mathbb{Z}\ |\ n = m^2\}\)
- \(\{(m, n) \in \mathbb{Z} \times \mathbb{Z}\ |\ n = m^2 - 5\}\)
Section 6.3
Progress Check 6.10
The functions \(k\), \(F\), and \(s\) are injections. The functions \(f\) and \(h\) are not injections.
Progress Check 6.11
The functions \(f\) and \(s\) are surjections. The functions \(k\) and \(F\) are not surjections.
Progress Check 6.15
The function \(f\) is an injection but not a surjection. To see that it is an injection, let \(a, b \in \mathbb{R}\) and assume that \(f(a) = f(b)\). This implies that \(e^{-a} = e^{-b}\). Now use the natural logarithm function to prove that \(a = b\). Since \(e^{-x} > 0\) for each real number \(x\), there is no \(x \in \mathbb{R}\) such that \(f(x) = -1\). So \(f\) is not a surjection.
The function \(g\) is an injection and is a surjection. The proof that g is an injection is basically the same as the proof that \(f\) is an injection. To prove that g is a surjection, let \(b \in R_{+}\). To construct the real number a such that g.a/ D b, solve the equation \(e^{-a} = b\) for \(a\). The solution is \(a = -\text{ln}b\). It can then be verified that \(g(a) = b\).
Progress Check 6.16
- There are several ordered pairs \((a, b) \in \mathbb{R} \times \mathbb{R}\) such that \(g(a, b) = 2\). For example, \(g(0, 2) = 2\), \(g(-1, 4) = 2\), and \(g(2, -2) = 2\).
- For each \(z \in \mathbb{R}\), \(g(0, z) = z\).
- Part (1) implies that the function \(g\) is not an injection. Part (2) implies that the function \(g\) is a surjection since for each \(z \in \mathbb{R}\), (\(0, z\)) is in the domain of \(g\) and \(g(0, z) = z\).
Section 6.4
Progress Check 6.17
The arrow diagram for \(g \circ f: A \to B\) should show the following:
\(\begin{array} {rclcrcl} {(g \circ f)(a)} &= & {g(f(a))} & & {(g \circ f)(b)} &= & {g(f(b))} \\ {} &= & {g(2) = 1} & & {} &= & {g(3) = 2} \\ {(g \circ f)(c)} &= & {g(f(c))} & & {(g \circ f)(d)} &= & {g(f(d))} \\ {} &= & {g(1) = 3} & & {} &= & {g(2) = 1} \end{array}\)
The arrow diagram for \(g \circ g: B \to B\) should show the following:
\(\begin{array} {rclcrcl} {(g \circ f)(1)} &= & {g(g(1))} & & {(g \circ g)(2)} &= & {g(g(2))} \\ {} &= & {g(3) = 2} & & {} &= & {g(1) = 3} \\ {(g \circ g)(3)} &= & {g(g(3))} & & {} & & {g(f(d))} \\ {} &= & {g(2) = 1} & & {} & & {} \end{array}\)
Progress Check 6.18
- \(F = g \circ f\), where \(f: \mathbb{R} \to \mathbb{R}\) by \(f(x) = x^2 + 3\), and \(g: \mathbb{R} \to \mathbb{R}\) by \(g(x) = x^3\).
- \(G = h \circ f\), where \(f: \mathbb{R} \to \mathbb{R}^{+}\) by \(f(x) = x^2 + 3\), and \(h: \mathbb{R}^{+} \to \mathbb{R}\) by \(h(x) = \text{In}x\).
- \(f = g \circ k\), where \(k: \mathbb{R} \to \mathbb{R}\) by \(k(x) = x^2 - 3\), and \(g: \mathbb{R} \to \mathbb{R}\) by \(g(x) = |x|\).
- \(g = h \circ f\), where \(f: \mathbb{R} \to \mathbb{R}\) by \(f(x) = \dfrac{2x - 3}{x^2 + 1}\), and \(h: \mathbb{R} \to \mathbb{R}\) by \(h(x) = \text{cos} x\).
Progress Check 6.19
For the examples that are constructed:
- \(g \circ f\) should be an injection.
- \(g \circ f\) should be a surjection.
- \(g \circ f\) should be a bijection.
Section 6.5
Progress Check 6.23
Neither set can be used to define a function.
1. The set \(F\) does not satisfy the first condition of Theorem 6.22.
2. The set \(G\) does not satisfy the second condition of Theorem 6.22.
Progress Check 6.24
2. \(f^{-1} = \{(r, a), (p, b), (q, c)\}\)
\(h^{-1} = \{(p, a), (q, b), (r, c), (q, d)\}\)
\(g^{-1} = \{(p, a), (q, b), (p, c)\}\)
3. (a) \(f^{-1}\) is a function from \(C\) to \(A\).
(b) \(g^{-1}\) is not a function from \(C\) to \(A\) since \((p, a) \in g^{-1}\) and \((p, c) \in g^{-1}\).
(c) \(h^{-1}\) is not a function from \(C\) to \(B\) since \((q, b) \in h^{-1}\) and \((q, d) \in h^{-1}\).
5. In order for the inverse of a function \(F: S \to T\) to be a function from \(T\) to \(S\), the function \(F\) must be a bijection.
Section 6.6
Progress Check 6.30
- \(f(A) = \{s, t\}\)
- \(f(B) = \{f(x) \ |\ x \in b\} = \{x\}\)
- \(f^{-1}(C) = \{x \in S\ |\ f(x) \in C\} = \{a, b, c, d\}\)
- \(f^{-1}(D) = \{x \in S\ |\ f(x) \in D\} = \{a, d\}\)
Progress Check 6.32
- \(f(0) = 2\) \(f(2) = 6\) \(f(4) = 2\) \(f(6) = 6\)
\(f(1) = 3\) \(f(3) = 3\) \(f(5) = 3\) \(f(7) = 3\) - (a) \(f(A) = \{2, 3, 6\}\) \(f^{-1}(C) = \{0, 1, 3, 4, 5, 7\}\)
\(f(B) = \{2, 3, 6\}\) \(f^{-1}(D) = \{1, 3, 5, 7\}\) - (a) \(f(A) \cap f(B) = \{2\}\) \(f(A) \cap f(B) = \{2, 3, 6\}\)
So in this case, \(f(A \cap B) \subseteq f(A) \cap f(B)\).
(b) \(f(A) \cup f(B) = \{2, 3, 6\}\) \(f(A \cup B) = \{2, 3, 6\}\)
So in this case, \(f(A \cap B) \subseteq f(A \cup B)\).
(c) \(f^{-1}(C) \cap f^{-1}(D) = f^{-1}(C \cap D) = \{1, 3, 5, 7\}\). So in this case, \(f^{-1}(C \cap D) = f^{-1}(C) \cap f^{-1}(D)\).
(d) \(f^{-1}(C) \cup f^{-1}(D) = f^{-1}(C \cup D) = \{0, 1, 3, 4, 5, 7\}\). So in this case, \(f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)\). - \(f(A) = \{2, 3, 6\}\). Hence, \(f^{-1}(f(A)) = \{0, 1, 2, 3, 4, 5, 6, 7\}\). So in this case, \(A \subseteq f^{-1}(f(A))\).
Section 7.1
Progress Check 7.2
- (a) \(T\) is a relation on \(\mathbb{R}\) since \(S\) is a subset of \(\mathbb{R} \times \mathbb{R}\).
(b) Solve the equation \(x^2 + 4^2 = 64\). This gives \(x = \pm \sqrt 48\).
Solve the equation \(x^2 + 9^2 = 64\). There are no real number solutions. So there does not exist an \(x \in \mathbb{R}\) such that \((x, 9) \in S\).
(c) dom\((T) = \{x \in \mathbb{R}\ |\ -8 \le x \le 8\}\) range\((T) = \{y \in \mathbb{R}\ |\ -8 \le y \le 8\}\)
(d) The graph is a circle of radius 8 whose center is at the origin. - (a) \(R\) is a relation on \(A\) since \(R\) is a subset of \(A \times A\).
(b) If we assume that each state except Hawaii has a land border in common with itself, then the domain and range of \(R\) are the set of all states except Hawaii. If we do not make this assumption, then the domain and range are the set of all states except Hawaii and Alaska.
(c) The first statement is true. If x has a land border with y, then y has a land border with x. The second statement is false. Following is a counterexample: (Michigan, Indiana) \(\in R\), (Indiana, Illinois) \(\in R\), but (Michigan, Illinois) \(\notin R\).
Progress Check 7.3
- The domain of the divides relation is the set of all nonzero integers. The range of the divides relation is the set of all integers.
- (a) This statement is true since for each \(a \in \mathbb{Z}\), \(a = a\cdot 1\).
(b) This statement is false: For example, 2 divides 4 but 4 does not divide 2.
(c) This statement is true by Theorem 3.1 on page 88.
Progress Check 7.4
- Each element in the set \(F\) is an ordered pair of the form \((x, y)\) where \(y = x^2\).
- (a) \(A = \{-2, 2\}\)
(b) \(B = \{-\sqrt{10}, \sqrt{10}\}\)
(c) \(C = \{25\}\)
(d) \(D = \{9\}\) - The graph of \(y = x^2\) is a parabola with vertex at the origin that is concave up.
Progress Check 7.5
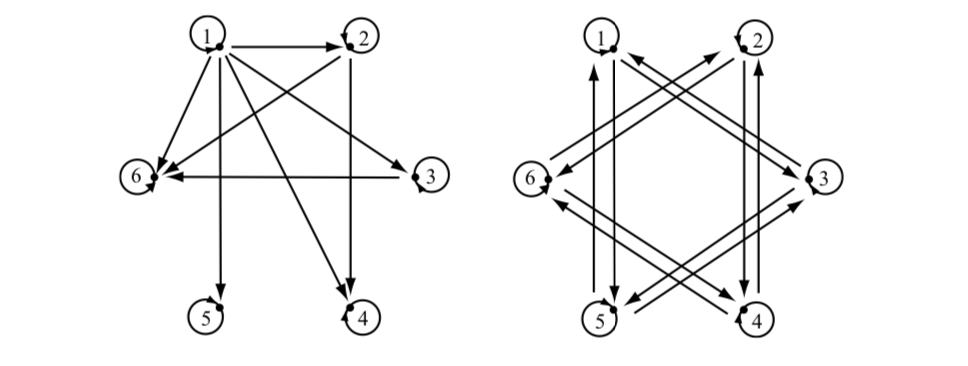
The directed graph for Part (a) is on the left and the directed graph for Part (b) is on the right.
Section 7.2
Progress Check 7.7
The relation \(R\):
- Is not reflexive since \((c, c) \notin R\) and \((d, d) \notin R\).
- Is symmetric.
- Is not transitive. For example, \((c, a) \in R\), \((a, c) \in R\), but \((c, c) \notin R\).
Progress Check 7.9
- Proof that the relation \(\sim\) is symmetric: Let \(a, b \in \mathbb{Q}\) and assume that \(a \sim b\). This means that \(a - b \in \mathbb{Z}\). Therefore, \(-(a - b) \in \mathbb{Z}\) and this means that \(b - a \in \mathbb{Z}\), and hence, \(b \sim a\).
- Proof that the relation \(\sim\) is transitive: Let \(a, b, c \in \mathbb{Q}\)and assume that \(a \sim b\) and \(b \sim c\). This means that \(a - b \in \mathbb{Z}\) and that \(b - c \in \mathbb{Z}\). Therefore, \(((a - b) + (b - c)) \in \mathbb{Z}\) and this means that \(a - c \in \mathbb{Z}\), and hence, \(a \sim c\).
Progress Check 7.11
The relation \(\thickapprox\) is reflexive on \(\mathcal{P}(U)\) since for all \(A \in \mathcal{P}(U)\), card(\(A\) )= card(\(A\)).
The relation \(\thickapprox\) is symmetric since for all \(A, B \in \mathcal{P}(U)\), if card(\(A\)) = card(\(B\)), then using the fact that equality on \(\mathbb{Z}\) is symmetric, we conclude that card(\(B\)) = card(\(A\)). That is, if \(A\) has the same number of elements as \(B\), then \(B\) has the same number of elements as \(A\).
The relation \(\thickapprox\) is transitive since for all \(A, B, C \in \mathcal{P}(U)\), if card(\(A\)) = card(\(B\)) and card(\(B\)) = card(\(C\)), then using the fact that equality on \(\mathbb{Z}\) is transitive, we conclude that card(\(A\)) = card(\(C\)). That is, if \(A\) and \(B\) have the same number of elements and \(B\) and \(C\) have the same number of elements, then \(A\) and \(C\) have the same number of elements.
Therefore, the relation \(\thickapprox\) is an equivalence relation on \(\mathcal{P}(U)\).
Section 7.3
Progress Check 7.12
The distinct equivalence classes for the relation \(R\) are: \(\{a, b, e\}\) and \(\{c, d\}\).
Progress Check 7.13
The distinct congruence classes for congruence modulo 4 are
[0] = {..., -12, -8, -4, 0, 4, 8, 12, ...} [1] = {..., -11, -7, -3, 1, 5, 9, 13, ...}
[2] = {..., -10, -6, -2, 2, 6, 10, 14, ...} [1] = {..., -9, -5, -1, 3, 7, 11, 15, ...}
Progress Check 7.15
- [5] = [-5] = {-5, 5} [\(\pi\)] = [-\(\pi\)] = {-\(\pi\), \(\pi\)}
[10] = [-10] = {-10, 10} - [0] = {0}
- [\(a\)] = {-\(a\), \(a\)}
Section 7.4
Progress Check 7.2
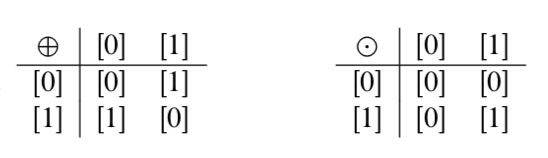
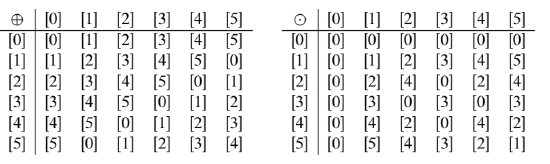
- For all \(a, b \in \mathbb{Z}\), if \(a \ne 0\) and \(b \ne 0\), then \(ab \ne 0\).
- The statement in (a) is true and the statement in (b) is false. For example, in \(\mathbb{Z}_{6}\), \([2] \odot [3] = [0]\).
Section 8.1
Progress Check 8.2
- The remainder is 8.
- gcd(12, 8) = 4
- \(12 = 8 \cdot 1 + 4\) and gcd(\(r\), \(r_2\)) = gcd(8, 4) = 4.
Progress Check 8.4
-
Original Pair Equation from Division Algorithm New Pair (180, 126) \(180 = 126 \cdot 1 + 54\) (126, 54) (126, 54) \(126 = 54 \cdot 2 + 18\) (54, 18) (54, 18) \(54 = 18 \cdot 3 + 0\) Consequently, gcd(180, 126) = 18.
-
Original Pair Equation from Division Algorithm New Pair (4208, 288) \(4208 = 288 \cdot 14 + 176\) (288, 176) (288, 176) \(288 = 126 \cdot 1+ 112\) (176, 112) (176, 112) \(176 = 112 \cdot 1+ 64\) (112, 64) (112, 64) \(112 = 64 \cdot 1+ 48\) (64, 48) (64, 48) \(64 = 48 \cdot 1+ 16\) (48, 16) (48, 16) \(48 = 16 \cdot 3+ 0\) Consequently, gcd(4208. 288) = 16.
Progress Check 8.7
- From Progress Check 8.4, gcd(180, 126) = 18.
\[\begin{array}{rcl} {18} &= & {126 - 54 \cdot 2} \\ {} &= & {126 - (180 - 126) \cdot 2} \\ {} &= & {126 \cdot 3 + 180 \cdot (-2)} \end{array}\]
So gcd(180, 126) = 18, and \(18 = 126 \cdot 3 + 180 \cdot (-2)\). - From Progress Check 8.4, gcd(4208. 288) = 16.
\[\begin{array}{rcl} {16} &= & {64 - 48} \\ {} &= & {64 - (112 - 64) = 64 \cdot 2 - 112} \\ {} &= & {(176 - 112) \cdot 2 - 112 = 176 \cdot 2 - 112 \cdot 3} {} &= & {176 \cdot 2 - (288 - 176) \cdot 3 = 176 \cdot 5 - 288 \cdot 3} \\ {} &= & {(4208 - 288 \cdot 14) \cdot 5 - 288 \cdot 3} \\ {} &= & {4208 \cdot 5 + 288 \cdot (-73)} \end{array}\]
So gcd(4208. 288) = 16, and \(16 = 4208 \cdot 5 + 288 \cdot (-73)\).
Section 8.2
Progress Check 8.10
- If \(a, p \in \mathbb{Z}\), \(p\) is prime, and \(p\) divides \(a\), then gcd(\(a\), \(p\)) = \(p\).
- If \(a, p \in \mathbb{Z}\), \(p\) is prime, and \(p\) does not divide \(a\), then gcd(\(a\), \(p\)) = 1.
- Three examples are gcd(4, 9) = 1, gcd(15, 16) = 1, gcd(8, 25) = 1.
Progress Check 8.13
Theorem 8.12. Let \(a\), \(b\), and \(c\) be integers. If \(a\) and \(b\) are relatively prime and \(a\ |\ (bc)\). We will prove that \(a\) divides \(c\).
Proof. Let \(a\), \(b\), and \(c\) be integers. Assume that \(a\) and \(b\) are relatively prime and \(a\ |\ (bc)\). We will prove that \(a\) divides \(c\).
Since \(a\) divides \(bc\), there exists an integer \(k\) such that
\[bc = ak.\]
In addition, we are assuming that \(a\) and \(b\) are relatively prime and hence gcd(\(a\), \(b\)) = 1. So by Theorem 8.9, there exist integers \(m\) and \(n\) such that
\[am + bn = 1.\]
We now multiply both sides of equation (B.21) by \(c\). This gives
\[\begin{array} {rcl} {(am + bn)c} &= & {1 \cdot c} \\ {acm + bcn} &= & {c} \end{array}\]
We can now use equation (B.20) to substitute \(bc = ak\) in equation (B.22) and obtain
\(acm + akn = c.\)
If we now factor the left side of this last equation, we see that \(a(cm + kn) = c\). Since (\(cm + kn\)) is an integer, this proves that \(a\) divides \(c\). Hence, we have proven that if a and b are relatively prime and \(a\ |\ (bc)\), then \(a\ |\ c\).
Section 8.3
Progress Check 8.20
2. \(x = 2 + 3k\) and \(y = 0 - 2k\), where \(k\) can be any integer. Again, this does not prove that these are the only solutions.
Progress Check 8.21
One of the Diophantine equations in Preview Activity 2 was \(3x + 5y = 11\). We were able to write the solutions of this Diophantine equation in the form
\(x = 2 + 5k\) and \(y = 1 - 3k\),
where \(k\) is an integer. Notice that \(x = 2\) and \(y = 1\) is a solution of this equation. If we consider this equation to be in the form \(ax + by = c\), then we see that \(a = 3\), \(b = 5\), and \(c = 11\). Solutions for this equation can be written in the form
\(x = 2 + bk\) and \(y = 1 - ak\),
where \(k\) is an integer.
The other equation was \(4x + 6y = 16\). So in this case, \(a = 4\), \(b = 6\), and \(c = 16\). Also notice that \(d = \text{gcd}(4, 6) = 2\). We note that \(x = 4\) and \(y = 0\) is one solution of this Diophantine equation and solutions can be written in the form
\(x = 4 + 3k\) and \(y = 0 - 2k\),
where \(k\) is an integer. Using the values of \(a\), \(b\), and \(d\) given above, we see that the solutions can be written in the form
\(x = 2 + \dfrac{b}{d}k\) and \(y = 0 - \dfrac{a}{d}\),
where \(k\) is an integer.
Progress Check 8.24
- Since 21 does not divide 40, Theorem 8.22 tells us that the Diophantine equation \(63x + 336y = 40\) has no solutions. Remember that this means there is no ordered pair of integers (\(x\), \(y\)) such that \(63x + 336y = 40\). However, if we allow \(x\) and \(y\) to be real numbers, then there are real number solutions. In fact, we can graph the straight line whose equation is \(63x + 336y = 40\) in the Cartesian plane. From the fact that there is no pair of integers \(x\), \(y\) such that \(63x + 336y = 40\), we can conclude that there is no point on the graph of this line in which both coordinates are integers.
- To write formulas that will generate all the solutions, we first need to find one solution for \(144x + 225y = 27\). This can sometimes be done by trial and error, but there is a systematic way to find a solution. The first step is to use the Euclidean Algorithm in reverse to write gcd(144, 225) as a linear combination of 144 and 225. See Section 8.1 to review how to do this. The result from using the Euclidean Algorithm in reverse for this situation is
\[144 \cdot 11 + 225 \cdot (-7) = 9.\]
If we multiply both sides of this equation by 3, we obtain
\[144 \cdot 33 + 225 \cdot (-21) = 27.\]
This means that \(x_0 = 33\), \(y_0 = -21\) is a solution of the linear Diophantine equation \(144x + 225y = 27\). We can now use Theorem 8.22 to conclude that all solutions of this Diophantine equation can be written in the form
\[x = 33 + \dfrac{225}{9}k\ \ \ \ \ \ \ \ \ y = -21 - \dfrac{144}{9}k,\]
where \(k \in \mathbb{Z}\).
We check this general solution as follows: Let \(k \in \mathbb{Z}\). Then
\[\begin{array} {rcl} {144x + 225y} &= & {144(33 + 25k) + 225(-21 - 16k)} \\ {} &= & {(4752 + 3600k) + (-4725 - 3600k)} \\ {} &= & {27.} \end{array}\]
Section 9.1
Progress Check 9.2
- We first prove that \(f: A \to B\) is an injection. So let \(x, y \in A\) and assume that \(f(x) = f(y)\). Then \(x + 350 = y + 350\) and we can conclude that \(x = y\). Hence, \(f\) is an injection. To prove that \(f\) is a surjection, let \(b \in B\). Then \(351 \le b \le 450\) and hence, \(1 \le b - 350 \le 100\) and so \(b - 350 \in A\). In addtion, \(f(b - 350) = (b - 350) + 350 = b\). This proves that \(f\) is a surjection, Hence, the function \(f\) is a bijection, and so, \(A \thickapprox B\).
- If \(x\) and \(t\) are even integers and \(F(x) = F(t)\), then \(x + 1 = t + 1\) and, hence, \(x = t\). Therefore, \(F\) is an injection.
To prove that \(F\) is a surjection, let \(y \in D\). This means that \(y\) is an odd integer and, hence, \(y - 1\) is an even integer. In addition,
\[F(y - 1) = (y - 1 + 1 = y.\]
Therefore, \(F\) is a surjection and hence, \(F\) is a bijection. We conclude that \(E \thickapprox D\). - Let \(x, t \in (0,1)\) and assume that \(f(x) = f(t)\). Then \(bx = bt\) and, thence, \(x = t\). Therefore, \(f\) is an injection.
To prove that \(f\) is a surjection, let \(y \in (0, b)\). Since \(0 < y < b\), we conclude that \(0 < \dfrac{y}{b} < 1\) and that
\[f(\dfrac{y}{b}) - b(\dfrac{y}{b}\) = y.\]
Therefore, \(f\) is a surjection and hence \(f\) is a bijection. Thus, \((0, 1) \thickapprox (0, b)\).
Section 9.2
Progress Check 9.11
- The set of natural numbers \(\mathbb{N}\) is a subset of \(\mathbb{Z}\), \(\mathbb{Q}\), and \(\mathbb{R}\). Since \(\mathbb{N}\) is an infinite set, we can use Part (2) of Theorem 9.10 to conclude that \(\mathbb{Z}\), \(\mathbb{Q}\), and \(\mathbb{R}\) are infinite sets.
- Use Part (1) of Theorem 9.10.
- Prove that \(\mathbb{E}^{+} \thickapprox \mathbb{N}\) and use Part (1) of Theorem 9.10.
Progress Check 9.12
- Use the definition of a countably infinite set.
- Since \(\mathbb{E}^{+} \thickapprox \mathbb{N}\), we can conclude that card\((E^{+}) = \aleph_{0}\).
- One function that can be used is \(f: S \to \mathbb{N}\) defined by \(f(m) = \sqrt{m}\) for all \(m \in S\).
Progress Check 9.23
Player Two has a winning strategy. On the \(k\)th turn, whatever symbol Player One puts in the \(k\)th position of the \(k\)th row, Player Two must put the other symbol in the \(k\)th position of his or her row. This guarantees that the row of symbols produced by Player Two will be different that any of the rows produced by Player One.
This is the same idea used in Cantor’s Diagonal Argument. Once we have a “list” of real numbers in normalized form, we create a real number that is not in the list by making sure that its \(k\)th decimal place is different than the \(k\)th decimal place for the \(k\)th number in the list. The one complication is that we must make sure that our new real number does not have a decimal expression that ends in all 9’s. This was done by using only 3’s and 5’s.
Progress Check 9.25
- Proof. In order to find a bijection \(f: (0, 1) \to (a, b)\), we will use the linear function through the points \((0, a)\) and \((1, b)\). The slope is \((b - a)\) and the \(y\)-intercept is \((0, a)\). So define \(f: (0, 1) \to (a, b)\) by
\[f(x) = (b - a) x + a, \text{for each } x \in (0, 1).\]
Now, if \(x, t \in (0, 1)\) and \(f(x) = f(t)\), then
\[(b - a)x + a = (b - a)t + a.\]
This implies that \((b - a) x = (b - a) t\), and since \(b - a \ne 0\), e can conclude that \(x = t\). Therefore, \(f\) is an injection.
To prove that \(f\) is a surjection, we let \(y \in (a, b)\). If \(x = \dfrac{y - a}{b - a}\), then
\[\begin{array} {rcl} {f(x)} &= & {f(\dfrac{y - a}{b - a})} \\ {} &= & {(b - a) (\dfrac{y - a}{b - a}) + a} \\ {} &= & {(y - a) + a} \\ {} &= & {y} \begin{array}\]
This proves that \(f\) is a surjection. Hence, \(f\) is a bijection and \((0, 1) \thickapprox (a, b)\). Therefore, \((a, b)\) is uncountable and has cardinality \(c\). - Now, if \(a, b, c, d\) are real number with \(a < b\) and \(c < d\), then we know that
\[(a, b) \thickapprox (0, 1) \text{ and } (c, d) \thickapprox (0, 1).\]
Since \(\thickapprox\) is an equivalence relation, we can conclude that \((a, b) \thickapprox (c, d)\).


