3.3: Indirect Proofs- Contradiction and Contraposition
- Page ID
- 19376
Suppose we are trying to prove that all thrackles are polycyclic1. A direct proof of this would involve looking up the definition of what it means to be a thrackle, and of what it means to be polycyclic, and somehow discerning a way to convert whatever thrackle’s logical equivalent is into the logical equivalent of polycyclic. As happens fairly often, there may be no obvious way to accomplish this task. Indirect proof takes a completely different tack. Suppose you had a thrackle that wasn’t polycyclic, and furthermore, show that this supposition leads to something truly impossible. Well, if it’s impossible for a thrackle to not be polycyclic, then it must be the case that all of them are. Such an argument is known as proof by contradiction.
Quite possibly the sweetest indirect proof known is Euclid’s proof that there are an infinite number of primes.
(Euclid) The set of all prime numbers is infinite.
- Proof
-
Suppose on the contrary that there are only a finite number of primes. This finite set of prime numbers could, in principle, be listed in ascending order.
\(\{p_1, p_2, p_3, . . . , p_n\})
Consider the number \(N\) formed by adding \(1\) to the product of all of these primes.
\(N = 1 + \prod_{k=1}^{n} p_k \)
Clearly, \(N\) is much larger than the largest prime \(p_n\), so \(N\) cannot be a prime number itself. Thus \(N\) must be a product of some of the primes in the list. Suppose that \(p_j\) is one of the primes that divides \(N\). Now notice that, by construction, \(N\) would leave remainder \(1\) upon division by \(p_j\). This is a contradiction since we cannot have both \(p_j |N\) and \(p_j ∤ N\).
Since the supposition that there are only finitely many primes leads to a contradiction, there must indeed be an infinite number of primes.
Q.E.D.
If you are working on proving a UCS and the direct approach seems to be failing you may find that another indirect approach, proof by contraposition, will do the trick. In one sense this proof technique isn’t really all that indirect; what one does is determine the contrapositive of the original conditional and then prove that directly. In another sense this method is indirect because a proof by contraposition can usually be recast as a proof by contradiction fairly easily.
The easiest proof I know of using the method of contraposition (and possibly the nicest example of this technique) is the proof of the lemma we stated in Section 1.6 in the course of proving that \(\sqrt{2}\) wasn’t rational. In case you’ve forgotten, we needed the fact that whenever \(x^2\) is an even number, so is \(x\).
Let’s first phrase this as a UCS.
\(∀x ∈ \mathbb{Z}, x^2 \text{ even } \implies x \text{ even}\)
Perhaps you tried to prove this result earlier. If so you probably came across the conceptual problem that all you have to work with is the evenness of \(x^2\) which doesn’t give you much ammunition in trying to show that \(x\) is even. The contrapositive of this statement is:
\(∀x ∈ \mathbb{Z}, x \text{ not even } \implies x^2 \text{ not even }\)
Now, since \(x\) and \(x^2\) are integers, there is only one alternative to being even – so we can re-express the contrapositive as
\(∀x ∈ \mathbb{Z}, x \text{ odd } \implies x^2 \text{ odd }.\)
Without further ado, here is the proof:
\[∀x ∈ \mathbb{Z}, x^2 \text{ even } \implies x \text{ even }\]
- Proof
-
This statement is logically equivalent to
\(∀x ∈ \mathbb{Z}, x \text{ odd } \implies x^2 \text{ odd }\)
so we prove that instead.
Suppose that \(x\) is a particular but arbitrarily chosen integer such that \(x\) is odd. Since \(x\) is odd, there is an integer \(k\) such that \(x = 2k + 1\). It follows that \(x^2 = (2k + 1)^2 = 4k^2 + 4k + 1 = 2(2k^2 + 2k) + 1\). Finally, we see that \(x^2\) must be odd because it is of the form \(2m + 1\), where \(m = 2k^2 + 2k\) is clearly an integer.
Q.E.D.
The main problem in applying the method of proof by contradiction is that it usually involves “cleverness.” You have to come up with some reason why the presumption that the theorem is false leads to a contradiction – and this may or may not be obvious. More than any other proof technique, proof by contradiction demands that we use drafts and rewriting. After monkeying around enough that we find a way to reach a contradiction, we need to go back to the beginning of the proof and highlight the feature that we will eventually contradict! After all, we want it to look like our proofs are completely clear, concise and reasonable even if their formulation caused us some sort of Gordian-level mental anguish.
We’ll end this section with an example from Geometry.
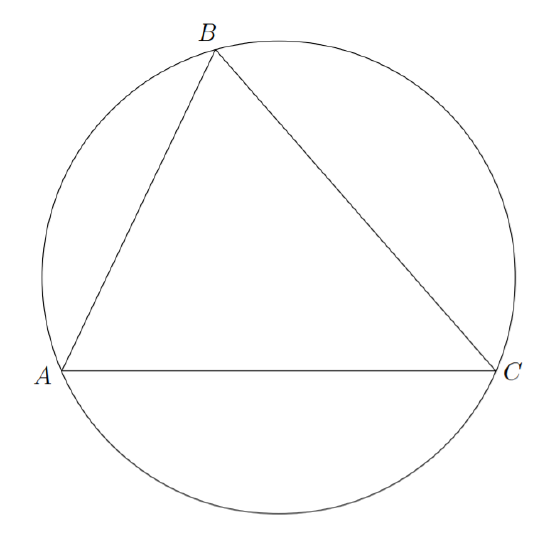
Among all triangles inscribed in a fixed circle, the one with maximum area is equilateral.
- Proof
-
We’ll proceed by contradiction. Suppose to the contrary that there is a triangle, \(\triangle ABC\), inscribed in a circle having maximum area that is not equilateral. Since \(\triangle ABC\) is not equilateral, there are two sides of it that are not equal. Without loss of generality, suppose that sides \(\overline{AB}\) and \(\overline{BC}\) have different lengths. Consider the remaining side (\(\overline{AC}\)) to be the base of this triangle. We can construct another triangle \(\triangle AB'C\), also inscribed in our circle, and also having \(\overline{AC}\) as its base, having a greater altitude than \(\triangle ABC\) — since the area of a triangle is given by the formula \(\dfrac{bh}{2}\) (where \(b\) is the base, and \(h\) is the altitude), this triangle’s area is evidently greater than that of \(\triangle ABC\). This is a contradiction since \(\triangle ABC\) was presumed to have maximal area.
We leave the actual construction \(\triangle AB'C\) to the following exercise.
Q.E.D.
Where should we place the point \(B'\) in order to create a triangle \(\triangle AB'C \) having greater area than any triangle such as \(\triangle ABC \) which is not isosceles?
Exercises:
Prove that if the cube of an integer is odd, then that integer is odd.
Prove that whenever a prime \(p\) does not divide the square of an integer, it also doesn’t divide the original integer. \((p ∤ x^2 \implies p ∤ x)\)
Prove (by contradiction) that there is no largest integer.
Prove (by contradiction) that there is no smallest positive real number.
Prove (by contradiction) that the sum of a rational and an irrational number is irrational.
Prove (by contraposition) that for all integers \(x\) and \(y\), if \(x + y\) is odd, then \(x \neq y\).
Prove (by contraposition) that for all real numbers \(a\) and \(b\), if \(ab\) is irrational, then \(a\) is irrational or \(b\) is irrational.
A Pythagorean triple is a set of three natural numbers, \(a\), \(b\) and \(c\), such that \(a^2 + b^2 = c^2\). Prove that, in a Pythagorean triple, at least one of \(a\) and \(b\) is even. Use either a proof by contradiction or a proof by contraposition.
Suppose you have \(2\) pairs of positive real numbers whose products are \(1\). That is, you have \((a, b)\) and \((c, d)\) in \(\mathbb{R}^2\) satisfying \(ab = cd = 1\). Prove that a < c implies that \(b > d\).


