6.3: Equivalence Relations
- Page ID
- 19397
The main idea of an equivalence relation is that it is something like equality, but not quite. Usually there is some property that we can name, so that equivalent things share that property. For example Albert Einstein and Adolf Eichmann were two entirely different human beings, if you consider all the different criteria that one can use to distinguish human beings there is little they have in common. But, if the only thing one was interested in was a person’s initials, one would have to say that Einstein and Eichmann were equivalent. Future examples of equivalence relations will be less frivolous. . . But first, the formal definition:
A relation \(\text{R}\) on a set \(S\) is an equivalence relation iff \(\text{R}\) is reflexive, symmetric and transitive.
Probably the most important equivalence relation we’ve seen to date is “congruence \(\text{mod } m\)” which we will denote using the symbol \(≡_m\). This relation may even be more interesting than actual equality! The reason for this seemingly odd statement is that “congruence \(\text{mod } m\)” gives us non-trivial equivalence classes. Equivalence classes are one of the most potent ideas in modern mathematics and it’s essential that you understand them, so we’ll start with an example. Consider congruence \(\text{mod } 5\). What other numbers is (say) \(11\) equivalent to? There are many! Any number that leaves the same remainder as \(11\) when we divide it by \(5\). This collection is called the equivalence class of \(11\) and is usually denoted using an overline \(\overline{11}\), another notation that is often seen for the set of things equivalent to \(11\) is \(11/ ≡_5\).
\(\overline{11} = \{. . . , −9, −4, 1, 6, 11, 16, . . .\}\)
It’s easy to see that we will get the exact same set if we choose any other element of the equivalence class (in place of \(11\)), which leads us to an infinite list of set equalities,
\(\overline{1} = \overline{6} = \overline{11} = . . .\)
And similarly,
\(\overline{2} = \overline{7} = \overline{12} = . . .\)
In fact, there are really just \(5\) different sets that form the equivalence classes \(\text{mod } 5\): \(\overline{0}\), \(\overline{1}\), \(\overline{2}\), \(\overline{3}\), and \(\overline{4}\). (Note: we have followed the usual convention of using the smallest possible non-negative integers as the representatives for our equivalence classes.)
What we’ve been discussing here is one of the first examples of a quotient structure. We start with the integers and “mod out” by an equivalence relation. In doing so, we “move to the quotient” which means (in this instance) that we go from \(\mathbb{Z}\) to a much simpler set having only five elements: \(\{0, 1, 2, 3, 4\}\). In moving to the quotient we will generally lose a lot of information, but greatly highlight some particular feature – in this example, properties related to divisibility by \(5\).
Given some equivalence relation \(\text{R}\) defined on a set \(S\) the set of equivalence classes of \(S\) under \(\text{R}\) is denoted \(S/\text{R}\) (which is read “\(S \text{ mod } \text{R}\)”). This use of the slash – normally reserved for division – shouldn’t cause any confusion since those aren’t numbers on either side of the slash but rather a set and a relation. This notation may also clarify why some people denote the equivalence classes above by \(0/ ≡_5\), \(1/ ≡_5\), \(2/ ≡_5\), \(3/ ≡_5\) and \(4/ ≡_5\).
The set of equivalence classes forms a partition of the set \(S\).
A partition \(P\) of a set \(S\) is a set of sets such that
\[S = \bigcup_{X∈P} X \;\;\; \text{ and } \;\;\; ∀X, Y ∈ P, X \neq Y \implies X ∩ Y = ∅.\]
In words, if you take the union of all the pieces of the partition you’ll get the set \(S\), and any pair of sets from the partition that aren’t identical are disjoint. Partitions are an inherently useful way of looking at things, although in the real world there are often problems (sets we thought were disjoint turn out to have elements in common, or we discover something that doesn’t fit into any of the pieces of our partition), in mathematics, we usually find that partitions do just what we would want them to do. Partitions divide some set up into a number of convenient pieces in such a way that we’re guaranteed that every element of the set is in one of the pieces and also so that none of the pieces overlap. Partitions are a useful way of dissecting sets, and equivalence relations (via their equivalence classes) give us an easy way of creating partitions – usually with some additional structure to boot! The properties that make a relation an equivalence relation (reflexivity, symmetry, and transitivity) are designed to ensure that equivalence classes exist and do provide us with the desired partition. For the beginning proof writer this all may seem very complicated, but take heart! Most of the work has already been done for you by those who created the general theory of equivalence relations and quotient structures. All you have to do (usually) is prove that a given relation is an equivalence relation by verifying that it is indeed reflexive, symmetric, and transitive. Let’s have a look at another example.
In Number Theory, the square-free part of an integer is what remains after we divide-out the largest perfect square that divides it. (This is also known as the radical of an integer.) The following table gives the square-free part, \(sf(n)\), for the first several values of \(n\).
| \(n\) | \(1\; 2\; 3\; 4\; 5\; 6 \;7\; 8\; 9 \;10 \;11 \;12\; 13\; 14\; 15 \;16 \;17 \;18\; 19 \;20\) | |||
| \(sf(n)\) | \(1 \;2\; 3 \;1 \;5 \;6 \;7 \;2 \;1 \;10 \;11 \;3 \;13\; 14 \;15 \;1 \;17 \;2 \;19\; 5\) | |||
It’s easy to compute the square-free part of an integer if you know its prime factorization – just reduce all the exponents \(\text{mod } 2\). For example1
\(808017424794512875886459904961710757005754368000000000 = 246 · 3 20 · 5 9 · 7 6 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71\)
the square-free part of this number is
\(5 · 13 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71 = 3504253225343845\)
which, while it is still quite a large number, is certainly a good bit smaller than the original!
We will define an equivalence relation \(\text{S}\) on the set of natural numbers by using the square-free part:
\(∀x, y ∈ \mathbb{N}, x\text{S}y \iff sf(x) = sf(y)\)
In other words, two natural numbers will be \(\text{S}\)-related if they have the same square-free parts.
What is \(1/\text{S}\)?
Before we proceed to the proof that \(\text{S}\) is an equivalence relation we’d like you to be cognizant of a bigger picture as you read. Each of the three parts of the proof will have a similar structure. We will show that \(\text{S}\) has one of the three properties by using the fact that \(=\) has that property. In more advanced work this entire proof could be omitted or replaced by the phrase “\(\text{S}\) inherits reflexivity, symmetry and transitivity from equality, and is therefore an equivalence relation.” (Nice trick isn’t it? But before you’re allowed to use it you have to show that you can do it the hard way . . . )
The relation \(\text{S}\) defined by
\[∀x, y ∈ \mathbb{N}, x\text{S}y \iff sf(x) = sf(y)\]
is an equivalence relation on \(\mathbb{N}\).
- Proof
-
We must show that \(\text{S}\) is reflexive, symmetric and transitive.
reflexive — (Here we must show that \(∀x ∈ \mathbb{N}, x\text{S}x\).) Let \(x\) be an arbitrary natural number. Since \(sf(x) = sf(x)\) (this is the reflexive property of \(=\)) it follows from the definition of \(\text{S}\) that \(x\text{S}x\).
symmetric — (Here we must show that \(∀x, y ∈ \mathbb{N}, x\text{S}y \implies y\text{S}x\).) Let \(x\) and \(y\) be arbitrary natural numbers, and further suppose that \(x\text{S}y\). Since \(x\text{S}y\), it follows from the definition of \(\text{S}\) that \(sf(x) = sf(y)\), obviously then \(sf(y) = sf(x)\) (this is the symmetric property of \(=\)) and so \(y\text{S}x\).
transitive — (Here we must show that \(∀x, y, z ∈ \mathbb{N}, x\text{S}y ∧ y\text{S}z \implies x\text{S}z\).) Let \(x\), \(y\) and \(z\) be arbitrary natural numbers, and further suppose that both \(x\text{S}y\) and \(y\text{S}z\). From the definition of \(\text{S}\) we deduce that \(sf(x) = sf(y)\) and \(sf(y) = sf(z)\). Clearly, \(sf(x) = sf(z)\) (this deduction comes from the transitive property of \(=\)), so \(x\text{S}z\).
Q.E.D.
We’ll end this section with an example of an equivalence relation that doesn’t “inherit” the three properties from equality.
A graph is a mathematical structure consisting of two sets, a set \(V\) of points (a.k.a. vertices) and a set2 \(E\) of edges. The elements of \(E\) may be either ordered or unordered pairs from \(V\). If \(E\) consists of ordered pairs we have a directed graph or digraph – the diagrams we have been using to visualize relations! If \(E\) consists of unordered pairs then we are dealing with an undirected graph. Since the undirected case is actually the more usual, if the word “graph” appears without a modifier it is assumed that we are talking about an undirected graph.
The previous paragraph gives a relatively precise definition of a graph in terms of sets, however the real way to think of graphs is in terms of diagrams where a set of dots are connected by paths. (The paths will, of course, need to have arrows on them in digraphs.) Below are a few examples of the diagrams that are used to represent graphs.
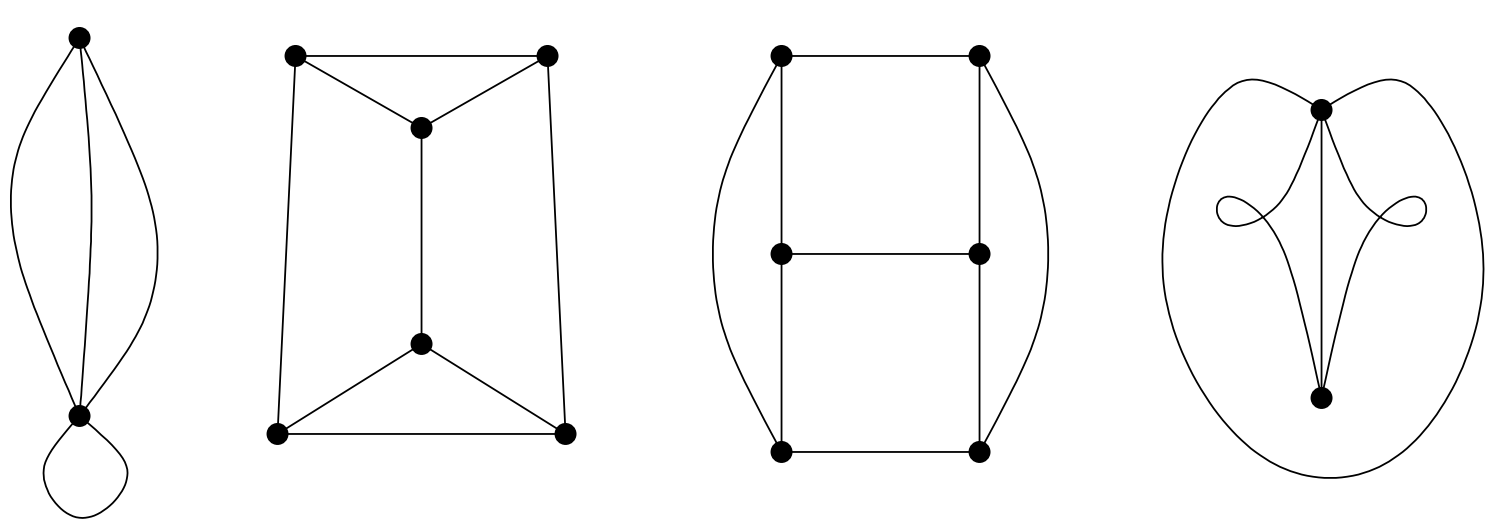
Two graphs are said to be isomorphic if they represent the same connections. There must first of all be a one-to-one correspondence between the vertices of the two graphs, and further, a pair of vertices in one graph are connected by some number of edges if and only if the corresponding vertices in the other graph are connected by the same number of edges.
The four examples of graphs above actually are two pairs of isomorphic graphs. Which pairs are isomorphic?
This word “isomorphic” has a nice etymology. It means “same shape.” Two graphs are isomorphic if they have the same shape. We don’t have the tools right now to do a formal proof (in fact we need to look at some further prerequisites before we can really precisely define isomorphism), but isomorphism of graphs is an equivalence relation. Let’s at least verify this informally.
Reflexivity: Is a graph isomorphic to itself? That is, does a graph have the “same shape” as itself? Clearly!
Symmetry: If graph \(A\) is isomorphic to graph \(B\), is it also the case that graph \(B\) is isomorphic to graph \(A\)? I.e. if \(A\) has the “same shape” as \(B\), doesn’t \(B\) have the same shape as \(A\)? Of course!
Transitivity: Well . . . the answer here is going to be “Naturally!” but let’s wait to delve into this issue when we have a usable formal definition for graph isomorphism. The question at this stage should be clear though: If \(A\) is isomorphic to \(B\) and \(B\) is isomorphic to \(C\), then isn’t \(A\) isomorphic to \(C\)?
Exercises:
Consider the relation \(\text{A}\) defined by
\(\text{A} = \{(x, y) x \text{ has the same astrological sign as } y\}\).
Show that \(\text{A}\) is an equivalence relation. What equivalence class under \(\text{A}\) do you belong to?
Define a relation \(\square\) on the integers by \(x\square y \iff x^2 = y^2\). Show that \(\square\) is an equivalence relation. List the equivalence classes \(x/ \square\) for \(0 ≤ x ≤ 5\).
Define a relation \(\text{A}\) on the set of all words by
\(w_1\text{A}w_2 \iff w_1 \text{ is an anagram of } w_2\).
Show that \(\text{A}\) is an equivalence relation. (Words are anagrams if the letters of one can be re-arranged to form the other. For example, ‘ART’ and ‘RAT’ are anagrams.)
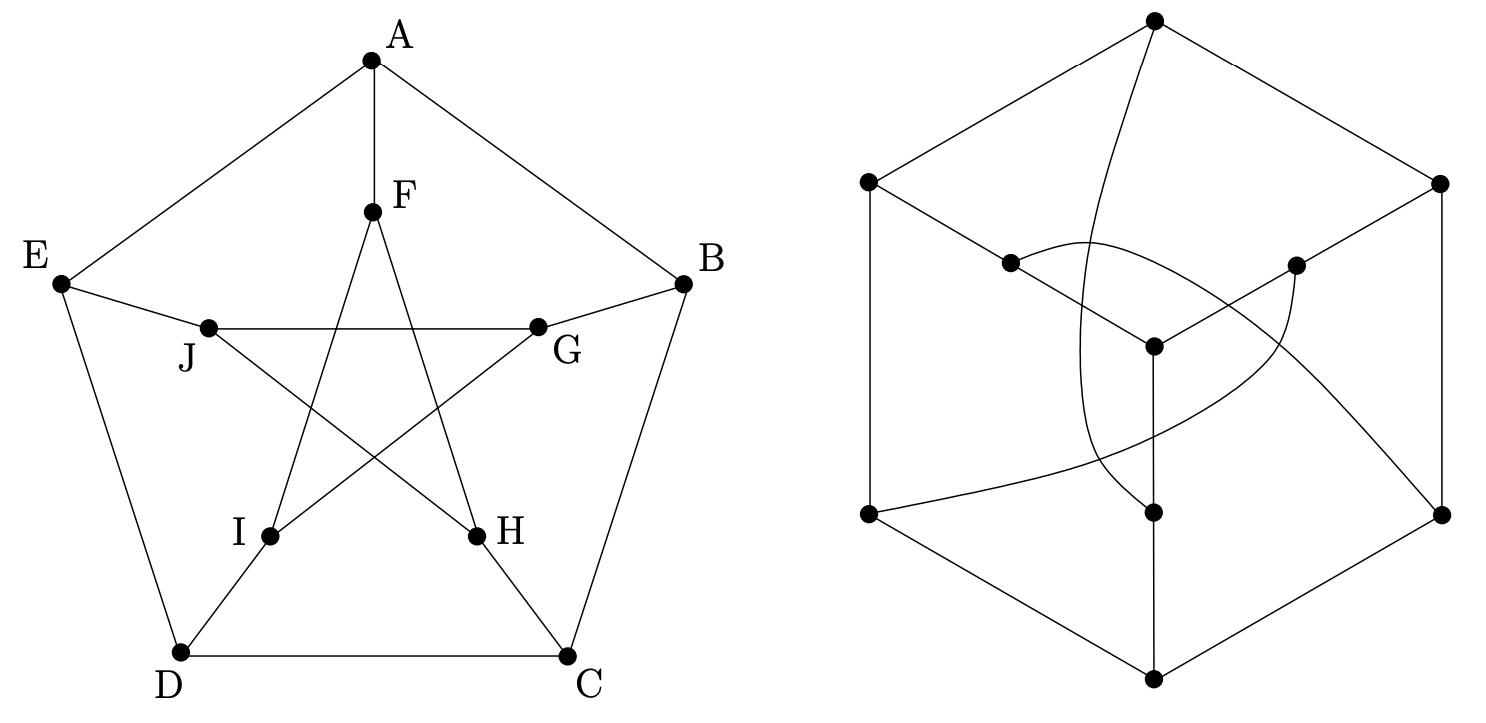
The two diagrams below both show a famous graph known as the Petersen graph. The picture on the left is the usual representation which emphasizes its five-fold symmetry. The picture on the right highlights the fact that the Petersen graph also has a three-fold symmetry. Label the right-hand diagram using the same letters (\(\text{A}\) through \(\text{J}\)) in order to show that these two representations are truly isomorphic.
We will use the symbol \(\mathbb{Z}^∗\) to refer to the set of all integers except \(0\). Define a relation \(\text{Q}\) on the set of all pairs in \(\mathbb{Z} × \mathbb{Z}^∗\) (pairs of integers where the second coordinate is non-zero) by \((a, b)\text{Q}(c, d) \iff ad = bc\). Show that \(\text{Q}\) is an equivalence relation.
The relation Q defined in the previous problem partitions the set of all pairs of integers into an interesting set of equivalence classes. Explain why
\(\mathbb{Q} = (\mathbb{Z} × \mathbb{Z}^∗)/\text{Q}\).
Ultimately, this is the “right” definition of the set of rational numbers!
Reflect back on the proof in problem 5. Note that we were fairly careful in assuring that the second coordinate in the ordered pairs is non-zero. (This was the whole reason for introducing the \(\mathbb{Z}^∗\) notation.) At what point in the argument did you use this hypothesis?


