6.6: Special Functions
- Page ID
- 19400
There are a great many functions that fail the horizontal line test which we nevertheless seem to have inverse functions for. For example, \(x^2\) fails HLT but \(\sqrt{x}\) is a pretty reasonable inverse for it – one just needs to be careful about the “plus or minus” issue. Also, \(\sin x\) fails HLT pretty badly; any horizontal line \(y = c\) with \(−1 ≤ c ≤ 1\) will hit \(\sin x\) infinitely many times. But look! Right here on my calculator is a button labeled “\(\sin^{−1}\).”1 This apparent contradiction can be resolved using the notion of restriction.
Given a function \(f\) and a subset \(D\) of its domain, the restriction of \(f\) to \(D\) is denoted \(f|_D\) and
\[f|_D = \{(x, y) x ∈ D ∧ (x, y) ∈ f\}.\]
The way we typically use restriction is to eliminate any regions in \(\text{Dom}(f)\) that cause \(f\) to fail to be one-to-one. That is, we choose a subset \(D ⊆ \text{Dom}(f)\) so that \(f|_D\) is an injection. This allows us to invert the restricted version of \(f\). There can be problems in doing this, but if we are careful about how we choose \(D\), these problems are usually resolvable.
Suppose \(f\) is a function that is not one-to-one, and \(D\) is a subset of \(\text{Dom}(f)\) such that \(f|_D\) is one-to-one. The restricted function \(f|_D\) has an inverse which we will denote by \(g\). Note that \(g\) is a function from \(\text{Rng}(f|_D)\) to \(D\). Which of the following is always true: \(f(g(x)) = x\) or \(g(f(x)) = x\)?
Technically, when we do the process outlined above (choose a domain \(D\) so that the restriction \(f|_D\) is invertible, and find that inverse) the function we get is a right inverse for \(f\).
Let’s take a closer look at the inverse sine function. This should help us to really understand the “right inverse” concept.
A glance at the graph of \(y = \sin x\) will certainly convince us that this function is not injective, but the portion of the graph shown in bold below passes the horizontal line test.
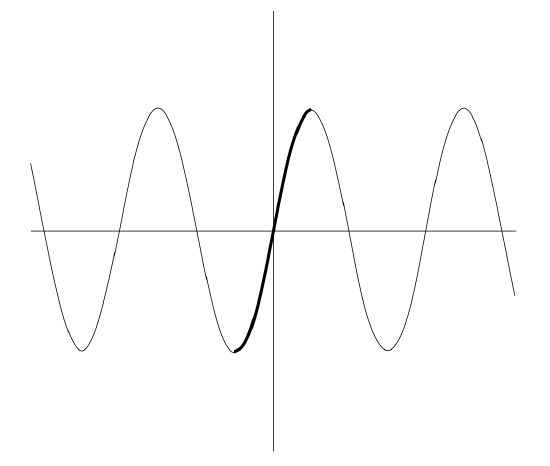
If we restrict the domain of the sine function to the closed interval \( \left[ −\dfrac{π}{2}, \dfrac{π}{2} \right]\), we have an invertible function. The inverse of this restricted function is the function we know as \(\sin^{−1} (x)\) or \(\arcsin(x)\). The domain and range of \(\sin^{−1} (x)\) are (respectively) the intervals \([−1, 1]\) and \(\left[ −\dfrac{π}{2}, \dfrac{π}{2} \right]\).
Notice that if we choose a number \(x\) in the range \(−1 ≤ x ≤ 1\) and apply the inverse sine function to it, we will get a number between \(-\dfrac{π}{2}\) and \(\dfrac{π}{2}\) – i.e. a number we can interpret as an angle in radian measure. If we then proceed to calculate the sine of this angle, we will get back our original number \(x\).
On the other hand, if we choose an angle first, then take the sine of it to get a number in \([−1, 1]\) and then take the inverse sine of that, we will only end up with the same angle we started with if we chose the original angle so that it lay in the interval \(\left[ −\dfrac{π}{2}, \dfrac{π}{2} \right]\).
We get a right inverse for the cosine function by restricting it to the interval \([0, π]\). What are the domain and range of \(\cos^{−1}\)?
The winding map is a function that goes from \(\mathbb{R}\) to the unit circle in the \(x\)–\(y\) plane, defined by
\[W(t) = (\cos t, \sin t).\]
One can think of this map as literally winding the infinitely long real line around and around the circle. Obviously, this is not an injection – there are an infinite number of values of \(t\) that get mapped to (for instance) the point \((1, 0)\), \(t\) can be any integer multiple of \(2π\).
What is the set \(W^{−1} (\{(0, 1)\})\)?
If we restrict \(W\) to the half-open interval \([0, 2π)\) the restricted function \(W [0,2π)\) is an injection. The inverse function is not easy to write down, but it is possible to express (in terms of the inverse functions of sine and cosine) if we consider the four cases determined by what quadrant a point on the unit circle may lie in.
Suppose \((x, y)\) represents a point on the unit circle. If \((x, y)\) happens to lie on one of the coordinate axes we have
\(W^{−1} ((1, 0)) = 0\\ W^{−1} ((0, 1)) = \dfrac{π}{2} \\ W^{−1} ((−1, 0)) = π \\ W^{−1} ((0, −1)) = \dfrac{3π}{2}.\)
If neither \(x\) nor \(y\) is zero, there are four cases to consider. Write an expression for \(W^{−1} ((x, y))\) using the cases
- \(x > 0 ∧ y > 0\),
- \(x < 0 ∧ y > 0\),
- \(x < 0 ∧ y < 0\) and
- \(x > 0 ∧ y < 0\).
This last example that we have done (the winding map) was unusual in that the outputs were ordered pairs. In thinking of this map as a relation (that is, as a set of ordered pairs) we have an ordered pair in which the second element is an ordered pair! Just for fun, here is another way of expressing the winding map:
\[W = \{(t,(\cos t, \sin t)) t ∈ \mathbb{R}\}\]
When dealing with very complicated expressions involving ordered pairs, or more generally, ordered \(n\)-tuples, it is useful to have a way to refer succinctly to the pieces of a tuple.
Let’s start by considering the set \(P = \mathbb{R} × \mathbb{R}\) — i.e. \(P\) is the \(x\)–\(y\) plane. There are two functions, whose domain is \(P\) that “pick out” the \(x\), and/or \(y\) coordinate. These functions are called \(π_1\) and \(π_2\), \(π_1\) is the projection onto the first coordinate and \(π_2\) is the projection onto the second coordinate.2
The function \(π_1 : \mathbb{R} × \mathbb{R} \implies \mathbb{R}\) known as projection onto the first coordinate is defined by
\[π_1((x, y)) = x.\]
The definition of \(π_2\) is entirely analogous. You should note that these projection functions are very bad as far as being one-to-one is concerned. For instance, the preimage of \(1\) under the map \(π_1\) consists of all the points on the vertical line \(x = 1\). That’s a lot of preimages! These guys are so far from being one-to-one that it seems impossible to think of an appropriate restriction that would become invertible. Nevertheless, there is a function that provides a right inverse for both \(π_1\) and \(π_2\). Now, these projection maps go from \(\mathbb{R} × \mathbb{R}\) to \(\mathbb{R}\) so an inverse needs to be a map from \(\mathbb{R}\) to \(\mathbb{R} × \mathbb{R}\). What is a reasonable way to produce a pair of real numbers if we have a single real number in hand? There are actually many ways one could proceed, but one reasonable choice is to create a pair where the input number appears in both coordinates. This is the so-called diagonal map, \(d : \mathbb{R} × \mathbb{R} \implies \mathbb{R}\), defined by \(d(a) = (a, a)\).
Which of the following is always true,
\(d(π_1((x, y)) = (x, y)\) or \(π_1(d(x)) = x?\)
There are a few other functions that it will be convenient to introduce at this stage. All of them are aspects of the characteristic function of a subset, so we’ll start with that.
Whenever we have a subset/superset relationship, \(S ⊆ D\), it is possible to define a function whose codomain is \(\{0, 1\}\) which performs a very useful task – if an input \(x\) is in the set \(S\) the function will indicate this by returning \(1\), otherwise it will return \(0\). The function which has this behavior is known as \(1_S\), and is called the characteristic function of the subset \(S\) (There are those who use the term indicator function of \(S\) for \(1_S\).) By definition, \(D\) is the domain of this function.
\(1_S : D \implies \{0, 1\}\)
\[1_S(x)=\left\{ \begin{array}{ll} 1\;\;\;\; \text{ if } x ∈ S \\ 0\;\;\;\; \text{ otherwise} \end{array} \right.\]
If you have the characteristic function of a subset \(S\), how can you create the characteristic function of its complement, \(\overline{S}\).
A characteristic function may be thought of as an embodiment of a membership criterion. The logical open sentence “\(x ∈ S\)” being true is the same thing as the equation “\(1_S(x) = 1\).” There is a notation, growing in popularity, that does the same thing for an arbitrary open sentence. The Iverson bracket notation uses the shorthand \([P(x)]\) to represent a function that sends any \(x\) that makes \(P(x)\) true to \(1\), and any inputs that make \(P(x)\) false will get sent to \(0\).
\[ [P(x)]=\left\{ \begin{array}{ll} 1\;\;\;\; \text{ if } P(x) \\ 0\;\;\;\; \text{ otherwise} \end{array} \right. \]
The Iverson brackets can be particularly useful in expressing and simplifying sums. For example, we can write \(\sum^{24}_{i=1} [2|i]\) to find the number of even natural numbers less than \(25\). Similarly, we can write \(\sum^{24}_{i=1} [3|i]\) to find the number of natural numbers less than \(25\) that are divisible by \(3\).
What does the following formula count?
\(\sum^{24}_{i=1} [2|i] + [3|i] − [6|i]\)
There is a much more venerable notation known as the Kronecker delta that can be thought of as a special case of the idea inherent in Iverson brackets. We write \(δ_{ij}\) as a shorthand for a function that takes two inputs, \(δ(i, j)\) is \(1\) if and only if \(i\) and \(j\) are equal.
\[ δ_{ij} =\left\{ \begin{array}{ll} 1\;\;\;\; \text{ if } i=j \\ 0\;\;\;\; \text{ otherwise} \end{array} \right. \]
The corresponding Iverson bracket would simply be \([i = j]\).
We’ll end this section with a function that will be especially important in Chapter 8. If we have an arbitrary subset of the natural numbers, we can associate it with an infinite string of \(0\)’s and \(1\)’s. By sticking a decimal point in front of such a thing, we get binary notation for a real number in the interval \([0, 1]\). There is a subtle problem that we’ll deal with when we study this function in more detail in Chapter 8 — some real numbers can be expressed in two different ways in base \(2\). For example, \(\dfrac{1}{2}\) can either be written as \(.1\) or as \(.01\) (where, as usual, the overline indicates a pattern that repeats forever). For the moment, we are talking about defining a function \(\phi\) whose domain is \(\mathcal{P}(\mathbb{N})\) and whose codomain is the set of all infinite binary strings. Let us denote these binary expansions by .\(b_1b_2b_3b_4 . . .\). Suppose \(A\) is a subset of \(\mathbb{N}\), then the binary expansion associated with \(A\) will be determined by \(b_i = 1_A(i)\). (Alternatively, we can use the Iverson bracket notation: \(b_i = [i ∈ A]\).)
The function \(\phi\) defined in the last paragraph turns out to be a bijection – given a subset we get a unique binary expansion, and given binary expansion we get (using \(\phi^{-1}\)) a unique subset of \(\mathbb{N}\).
A few examples will probably help to clarify this function’s workings. Consider the set \(\{1, 2, 3\} ⊆ \mathbb{N}\), the binary expansion that this corresponds to will have \(1\)’s in the first three positions after the decimal – \(\phi (\{1, 2, 3\}) = .111\) this is the number written \(.875\) in decimal. The infinite repeating binary number \(.01\) is the base-\(2\) representation of \(\dfrac{1}{3}\), it is easy to see that .01 is the image of the set of odd naturals, \(\{1, 3, 5, . . .\}\).
Find the binary representation for the real number which is the image of the set of even numbers under \(\phi\).
Find the binary representation for the real number which is the image of the set of triangular numbers under \(\phi\). (Recall that the triangular numbers are \(T = \{1, 3, 6, 10, 15, . . .\}\).)
Exercises:
The \(n\)-th triangular number, denoted \(T(n)\), is given by the formula \(T(n) = \dfrac{(n^2 + n)}{2}\). If we regard this formula as a function from \(\mathbb{R}\) to \(\mathbb{R}\), it fails the horizontal line test and so it is not invertible. Find a suitable restriction so that \(T\) is invertible.
The usual algebraic procedure for inverting \(T(x) = \dfrac{(x^2+x)}{2}\) fails. Use your knowledge of the geometry of functions and their inverses to find a formula for the inverse. (Hint: it may be instructive to first invert the simpler formula \(S(x) = \dfrac{x^2}{2}\) — this will get you the right vertical scaling factor.)
What is \(π_2(W(t))\)?
Find a right inverse for \(f(x) = |x|\).
In three-dimensional space, we have projection functions that go onto the three coordinate axes (\(π_1\), \(π_2\) and \(π_3\)) and we also have projections onto coordinate planes. For example, \(π_{12}: \mathbb{R} × \mathbb{R} × \mathbb{R} \implies \mathbb{R} × \mathbb{R}\), defined by
\(π_{12}((x, y, z)) = (x, y)\)
is the projection onto the \(x\)–\(y\) coordinate plane. The triple of functions \((\cos t, \sin t, t)\) is a parametric expression for a helix. Let \(H = \{(\cos t, \sin t, t) t ∈ \mathbb{R} \}\) be the set of all points on the helix. What is the set \(π_{12}(H)\)? What are the sets \(π_{13}(H)\) and \(π_{23}(H)\)?
Consider the set \(\{1, 2, 3, . . . , 10\}\). Express the characteristic function of the subset \(S = \{1, 2, 3\}\) as a set of ordered pairs.
If \(S\) and \(T\) are subsets of a set \(D\), what is the product of their characteristic functions \(1_S · 1_T\)?
Evaluate the sum
\(\sum^{10}_{i=1} \dfrac{1}{i} · [i \text{ is prime}].\)


