7.4: The Algebra of Combinations
- Page ID
- 19405
Earlier in this chapter we determined the number of \(k\)-subsets of a set of size \(n\). These numbers, denoted by \(C(n, k) = nCk = \binom{n}{k}\) and determined by the formula \(\dfrac{n!}{k!(n−k)!}\) are known as binomial coefficients. It seems likely that you will have already seen the arrangement of these binomial coefficients into a triangular array – known as Pascal’s triangle, but if not...
\(1\)
\(1\;\; 1\)
\(1\;\; 2 \;\;1\)
\(1 \;\;3\;\; 3 \;\;1\)
\(1\;\; 4 \;\;6 \;\;4\;\; 1\)
\(1\;\; 5 \;\;10 \;\;10\;\; 5\;\; 1\)
\(1\;\; 6\;\; 15 \;\;20\;\; 15 \;\;6\;\;1\)
et cetera.
The thing that makes this triangle so nice and that leads to the strange name “binomial coefficients” for the number of \(k\)-combinations of an \(n\)-set is that you can use the triangle to (very quickly) compute powers of binomials.
A binomial is a polynomial with two terms. Things like \((x + y)\), \((x + 1)\) and \((x^7 + x^3)\) all count as binomials but to keep things simple just think about \((x + y)\). If you need to compute a large power of \((x + y)\) you can just multiply it out, for example, think of finding the \(6^{\text{th}}\) power of \((x + y)\).
We can use the F.O.I.L rule to find \((x + y)^2 = x^2 + 2xy + y^2\). Then \((x + y)^3 = (x + y) · (x + y)^2 = (x + y) · (x^2 + 2xy + y^2)\).
You can compute that last product either by using the distributive law or the table method
| \(x^2 +2xy +y^2\) | ||
| \(x\) | ||
| \(+y\) | ||
Either way, the answer should be \((x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3\).
Finally, the sixth power is the square of the cube thus
\((x + y)^6 = (x + y)^3 · (x + y)^3 = (x^3 + 3x^2y + 3xy^2 + y^3) · (x^3 + 3x^2 y + 3xy^2 + y^3 )\)
For this product I wouldn’t even think about the distributive law, I’d jump to the table method right away:
| \(x^3\) | \(+3x^2 y\) | \(+3xy^2\) | \(+y^3\) | |
| \(x^3\) | ||||
| \(+3x^2 y\) | ||||
| \(+3xy^2\) | ||||
| \(+y^3\) | ||||
In the end, you should obtain
\(x^6 + 6x^5 y + 15x^4 y^2 + 20x^3 y^3 + 15x^2 y^4 + 6xy^5 + y^6\).
Now all of this is a lot of work and it’s really much easier to notice the form of the answer: The exponent on \(x\) starts at \(6\) and descends with each successive term down to \(0\). The exponent on \(y\) starts at \(0\) and ascends to \(6\). The coefficients in the answer are the numbers in the sixth row of Pascal’s triangle.
Finally, the form of Pascal’s triangle makes it really easy to extend. A number in the interior of the triangle is always the sum of the two above it (on either side). Numbers that aren’t in the interior of the triangle are always \(1\).
We showed rows \(0\) through \(6\) above. Rows \(7\) and \(8\) are
\(1\;\; 7 \;\;21\;\; 35\;\; 35\;\; 21 \;\;7 \;\;1\)
\(1\;\; 8 \;\;28\;\; 56\;\; 70\;\; 56\;\; 28\;\; 8\;\; 1.\)
With this information in hand, it becomes nothing more than a matter of copying down the answer to compute
\((x+y)^8 = x^8+8x^7 y+28x^6 y^2+56x^5 y^3+70x^4 y^4+56x^3 y^5+28x^2 y^6+8xy^7+y^8 .\)
Given the method using Pascal’s triangle for computing \((x + y)\) n we can use substitution to determine more general binomial powers. Find \((x^4 + x^2 )^5\).
All of the above hinges on the fact that one can compute a binomial coefficient by summing the two that appear to either side and above it in Pascal’s triangle. This fact is the fundamental relationship between binomial coefficients – it is usually called Pascal’s formula.
For all natural numbers \(n\) and \(k\) with \(0 < k ≤ n\),
\[\binom{n}{k} = \binom{n − 1}{k} + \binom{n − 1}{k − 1}. \]
We are going to prove it twice.
- Proof #1
-
(The first proof is a combinatorial argument.)
There are \(\binom{n}{k}\) subsets of size \(k\) of the set \(N = \{1, 2, 3, . . . , n\}\). We will partition these \(k\)-subsets into two disjoint cases: those that contain the final number, \(n\), and those that do not. Let
\[A = \{S ⊆ N |S| = k ∧ n \notin S\}\]
and, let
\[B = \{S ⊆ N |S| = k ∧ n ∈ S\}\]
Since the number \(n\) is either in a \(k\)-subset or it isn’t, these sets are disjoint and exhaustive. So the addition rule tells us that
\[\binom{n}{k} = |A| + |B|.\]
The set \(A\) is really just the set of all \(k\)-subsets of the \((n − 1)\)-set \(\{1, 2, 3, . . . , n − 1\}\), so \(|A| = \binom{n−1}{k}\).
Any of the sets in \(B\) can be obtained by adjoining the element \(n\) to a \(k−1\) subset of the \((n−1)\)-set \(\{1, 2, 3, . . . , n−1\}\), so \(|B| = \binom{n−1}{k−1}\).
Substituting gives us the desired result.
Q.E.D
- Proof #2
-
(The second proof is algebraic in nature.)
Consider the sum
\[ \binom{n-1}{k} + \binom{n − 1}{k − 1}.\]
Applying the formula we deduced in Section 7 we get
\[\begin{array} s \binom{n − 1}{k} + \binom{n − 1}{k − 1} &= \dfrac{(n − 1)!}{k!(n − 1 − k)!} + \dfrac{(n − 1)!}{(k − 1)!((n − 1) − (k − 1))!} \\ &= \dfrac{(n − 1)!}{k!(n − k − 1)!} + \dfrac{(n − 1)!}{(k − 1)!(n − k)!} \end{array}\]
A common denominator for these fractions is \(k!(n − k)!\). (We will have to multiply the top and bottom of the first fraction by \((n − k)\) and the top and bottom of the second fraction by \(k\).)
\[\begin{array} &&= \dfrac{(n − k)(n − 1)!}{k!(n − k)(n − k − 1)!} + \dfrac{k(n − 1)!}{k(k − 1)!(n − k)!} \\ &= \dfrac{(n − k)(n − 1)!}{k!(n − k)!} + \dfrac{k(n − 1)!}{k!(n − k)!} \\ &= \dfrac{(n − k)(n − 1)! + k(n − 1)!}{k!(n − k)!} \\ &= \dfrac{(n − k + k)(n − 1)!}{k!(n − k)!} \\ &= \dfrac{(n)(n − 1)!}{k!(n − k)!} \\ &= \dfrac{n!}{k!(n − k)!} \end{array}.\]
We recognize the final expression as the definition of \(\binom{n}{k}\), so we have proved that
\[\binom{n − 1}{k} + \binom{n − 1}{k − 1} = \binom{n}{k}.\]
Q.E.D
There are quite a few other identities concerning binomial coefficient that can also be proved in (at least) two ways. We will provide one or two other examples and leave the rest to you in the exercises for this section.
For all natural numbers \(n\) and \(k\) with \(0 < k ≤ n\),
\[ k · \binom{n}{k} = n · \binom{n − 1}{k − 1}.\]
Let’s try a purely algebraic approach first.
- Proof
-
Using the formula for the value of a binomial coefficient we get
\[k · \binom{n}{k} = k · \binom{n!}{k!(n − k)!}.\]
We can do some cancellation to obtain
\[k · \binom{n}{k} = \binom{n!}{(k − 1)!(n − k)!}.\]
Finally we factor-out an \(n\) to obtain
\[k · \binom{n}{k} = n · \binom{(n − 1)!}{(k − 1)!(n − k)!},\]
since \((n − k)\) is the same thing as \(((n − 1) − (k − 1))\) we have
\[k · \binom{n}{k} = n · \binom{(n − 1)!}{(k − 1)!((n − 1) − (k − 1))!} = n · \binom{n − 1}{k − 1} \]
Q.E.D.
A combinatorial argument usually involves counting something in two ways. What could that something be? Well, if you see a product in some formula you should try to imagine what the multiplication rule would say in that particular circumstance.
- Proof
-
Consider the collection of all subsets of size \(k\) taken from \(N = \{1, 2, 3, . . . , n\}\) in which one of the elements has been marked to distinguish it from the others in some way.1
We can count this collection in two ways using the multiplication rule.
Firstly, we could select a \(k\)-subset in \(\binom{n}{k}\) ways and then from among the \(k\) elements of the subset we could select one to be marked. By this analysis, there are \(\binom{n}{k} · k\) elements in our collection.
Secondly, we could select an element from the \(n\)-set which will be the “marked” element of our subset, and then choose the additional \(k − 1\) elements from the remaining \(n − 1\) elements of the \(n\)-set. By this analysis there are \(n· \binom{n−1}{k−1}\) elements in the collection we have been discussing.
Thus,
\[k · \binom{n}{k} = n · \binom{n − 1}{k − 1}\]
Q.E.D.
The final result that we’ll talk about actually has (at least) three proofs. One of which suffers from the fault that it is “like swatting a fly with a sledge hammer.”
The result concerns the sum of all the numbers in some row of Pascal’s triangle.
For all natural numbers \(n\) and \(k\) with \(0 < k ≤ n\),
\[\sum_{k=0}^{n} \binom{n}{k} = 2^n\]
Our sledgehammer is a powerful result known as the binomial theorem which is a formalized statement of the material we began this section with.
For all natural numbers \(n\), and real numbers \(x\) and \(y\),
\[(x + y)^n = \sum_{k=0}^{n} \binom{n}{k} = x^{n−k} y^k\]
- Proof
-
We won’t be proving this result just now. But, the following proof is a proof of the previous theorem using this more powerful result.
- Proof #1 (of Theorem \(7.4.3\))
-
Substitute \(x = y = 1\) in the binomial theorem.
Q.E.D.
Our second proof will be combinatorial. Let us re-iterate that a combinatorial proof usually consists of counting some collection in two different ways. The formula we have in this example contains a sum, so we should search for a collection of things that can be counted using the addition rule.
- Proof #2 (of Theorem \(7.4.3\))
-
The set of all subsets of \(N = \{1, 2, 3, . . . , n\}\), which we denote by \(\mathcal{P}(N)\), can be partitioned into \(n + 1\) sets based on the sizes of the subsets,
\[\mathcal{P}(N) = S_0 ∪ S_1 ∪ S_2 ∪ . . . ∪ S_n,\]
where \(S_k = \{S | S ⊆ N ∧ |S| = k\}\) for \(0 ≤ k ≤ n\). Since no subset of \(N\) can appear in two different parts of the partition (a subset’s size is unique) and every subset of \(N\) appears in one of the parts of the partition (the sizes of subsets are all in the range from \(0\) to \(n\)). The addition principle tells us that
\[|\mathcal{P}(N)| = |S_0| + |S_1| + ∪|S_2| + . . . + |S_n|.\]
We have previously proved that \(|\mathcal{P}(N)| = 2^n\) and we know that \(|S_k| = \binom{n}{k}\) so it follows that
\[2^n = \binom{n}{0} + \binom{n}{1} + \binom{n}{2} + . . . + \binom{n}{n}\]
Q.E.D.
Exercises:
Use the binomial theorem (with \(x = 1000\) and \(y = 1\)) to calculate \(1001^6\).
Find \((2x + 3)^5\)
Find \((x^2 + y^2 )^6\).
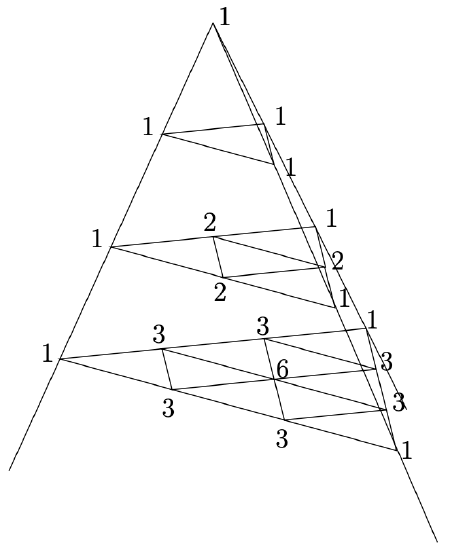
The following diagram contains a \(3\)-dimensional analog of Pascal’s triangle that we might call “Pascal’s tetrahedron.” What would the next layer look like?
The student government at Lagrange High consists of \(24\) members chosen from amongst the general student body of \(210\). Additionally, there is a steering committee of \(5\) members chosen from amongst those in student government. Use the multiplication rule to determine two different formulas for the total number of possible governance structures.
Prove the identity
\(\binom{n}{k} · \binom{k}{r} = \binom{n}{r} · \binom{n − r}{k − r} \)
combinatorially.
Prove the binomial theorem.
\(∀n ∈ \mathbb{N}, ∀_{x, y} ∈ \mathbb{R}, (x + y)^n = \sum^{n}_{k=0} \binom{n}{k} x^{n−k} y^k\)


