9.1: Morley’s Miracle
- Page ID
- 19416
Probably you have heard of the impossibility of trisecting an angle. (Hold on for a quick rant about the importance of understanding your hypotheses) What’s actually true is that you can’t trisect a generic angle if you accept the restriction of using the old-fashioned tools of Euclidean geometry: the compass and straight-edge. There are a lot of constructions that can’t be done using just a straight-edge and compass–angle trisection, duplication of a cube1, squaring a circle, constructing a regular heptagon, et cetera.
If you allow yourself to use a ruler– i.e. a straight-edge with marks on it (indeed you really only need two marks a unit distance apart) then angle trisection be done via what is known as a neusis construction. Nevertheless, because of the central place of Euclid’s Elements in mathematical training throughout the centuries, and thereby, a very strong predilection towards that which possible via compass and straight-edge alone, it is perhaps not surprising that a perfectly beautiful result that involved trisecting angles went undiscovered until \(1899\), when Frank Morley stated his Trisector Theorem. There is much more to this result than we will state here – so much more that the name "Morley’s Miracle" that has been given to the Trisector theorem is truly justified – but even the simple, initial part of this beautiful theory is arguably miraculous! To learn more about Morley’s theorem and its extension see [8].
So, let’s state the theorem!
Start with an arbitrary triangle \({\triangle}ABC\). Trisect each of its angles to obtain a diagram something like that in Figure \(9.1.1\).
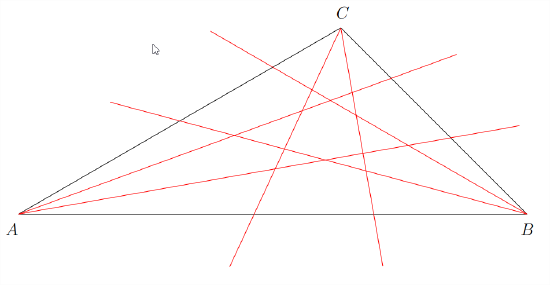
The six angle trisectors that we’ve just drawn intersect one another in quite a few points.
You could literally count the number of intersection points between the angle trisectors on the diagram, but you should also be able to count them (perhaps we should say “double-count them”) combinatorially. Give it a try!
Among the points of intersection of the angle trisectors there are three that we will single out – the intersections of adjacent trisectors. In Figure \(9.1.2\) the intersection of adjacent trisectors are indicated, additionally, we have connected them together to form a small triangle in the center of our original triangle.
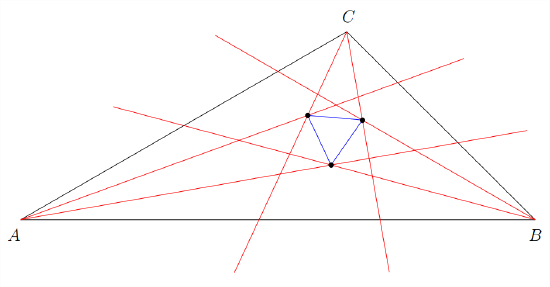
Are you ready for the miraculous part? Okay, here goes!
The points of intersection of the adjacent trisectors in an arbitrary triangle \(\triangle ABC\) form the vertices of an equilateral triangle.
In other words, that little blue triangle in Figure \(9.1.2\) that kind of like it might be equilateral actually does have all three sides equal to one another. Furthermore, it doesn’t matter what triangle we start with, if we do the construction above we’ll get a perfect \(60^\circ - 60^\circ - 60^\circ\) triangle in the middle!
Sources differ, but it is not clear whether Morley ever proved his theorem. The first valid proof (according to R. K. Guy in [8] was published in \(1909\) by M. Satyanarayana [15]. There are now other proofs known, for instance the cut-the-knot website (http://www.cut-the-knot.org/) exposits no less than nine different proofs. The proof by Satyanarayana used trigonometry. The proof we’ll look at here is arguably the shortest ever produced and it is due to John Conway. It is definitely a "Book proof"!
Let us suppose that an arbitrary triangle \(\triangle ABC\) is given. We want to show that the triangle whose vertices are the intersections of the adjacent trisectors is equilateral – this triangle will be referred to as the Morley triangle. Let’s also denote by \(A\), \(B\) and \(C\) the measures of the angles of \(\triangle ABC\). (This is what is generally known as an “abuse of notation” – we are intentionally confounding the vertices (\(A\), \(B\) and \(C\)) of the triangle with the measure of the angles at those vertices.) It turns out that it is fairly hard to reason from our knowledge of what the angles \(A\), \(B\) and \(C\) are to deduce that the Morley triangle is equilateral. How does the following plan sound: suppose we construct a triangle, that definitely does have an equilateral Morley triangle, whose angles also happen to be \(A\), \(B\) and \(C\). Such a triangle would be similar2 to the original triangle \(\triangle ABC\) – if we follow the similarity transform from the constructed triangle back to \(\triangle ABC\) we will see that their Morley triangles must coincide; thus if one is equilateral so is the other!
One of the features of Conway’s proof that leads to its great succinctness and beauty is his introduction of some very nice notation. Since we are dealing with angle trisectors, let \(a\), \(b\) and \(c\) be angles such that \(3a = A\), \(3b = B\) and \(3c = C\). Furthermore, let a superscript star denote the angle that is \(\dfrac{π}{3}\) (or \(60^{\circ}\) if you prefer) greater than a given angle. So, for example,
\[ a^{\star}= a + \dfrac{\pi}{3} \]
and
\[ a^{\star\star} = a + \dfrac{2}{3}. \]
Now, notice that the sum \(a+b+c\) must be \(\dfrac{\pi}{3}\). This is an immediate consequence of \(A+B+C=\pi\) which is true for any triangle in the plane. It follows that by distributing two stars amongst the three numbers \(a\), \(b\) and \(c\) we will come up with three quantities which sum to \(\pi\). In other words, there are Euclidean triangles having the following triples as their vertex angles:
\((a, b, c^{\star\star}) \;\;\;\;\;\;\;\;(a, b^{\star} , c^{\star} ) \\ (a, b^{\star\star}, c) \;\;\;\;\;\;\;\;(a^{\star} , b^{\star} , c) \\ (a^{\star\star}, b, c) \;\;\;\;\;\;\;\;(a^{\star}, b, c^{\star} )\)
In a nutshell, Conway’s proof consists of starting with an equilateral triangle of unit side length, adding appropriately scaled versions of the six triangles above and ending up with a figure (having an equilateral Morley triangle) similar to \({\triangle}ABC\). The generic picture is given in Figure \(9.1.3\). Before we can really count this argument as a proof, we need to say a bit more about what the phrase "appropriately scaled" means. In order to appropriately scale the triangles (the small acute ones) that appear green in Figure \(9.1.3\) we have a relatively easy job – just scale them so that the side opposite the trisected angle has length one; that way they will join perfectly with the central equilateral triangle.
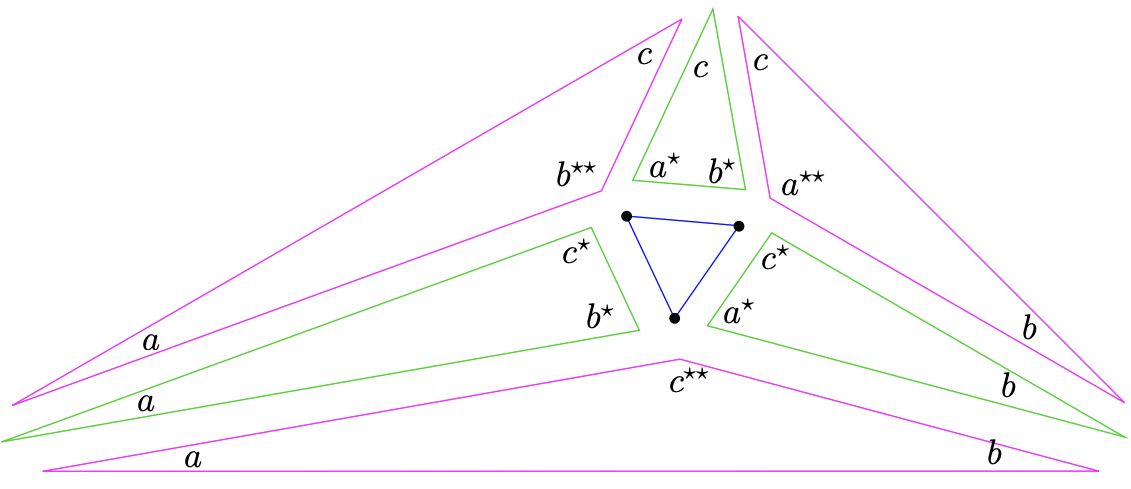
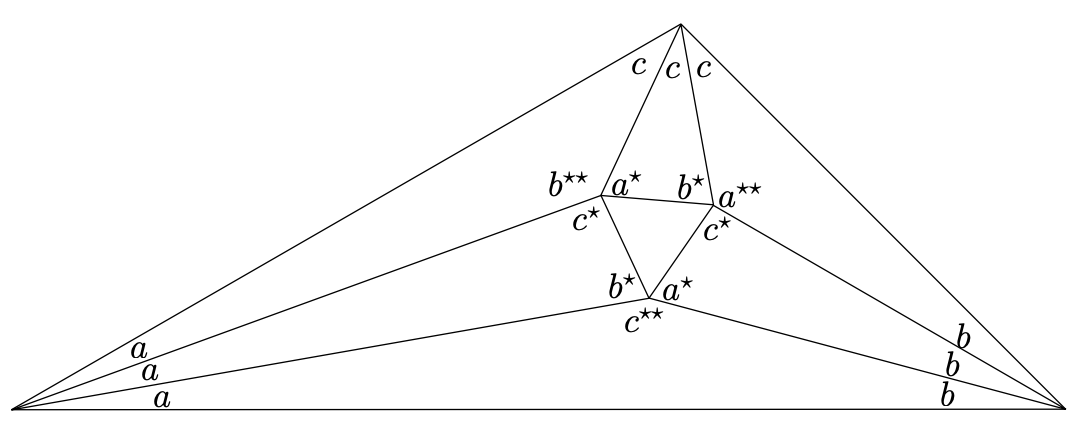
The triangles (these are the larger obtuse ones) that appear purple in Figure \(9.1.3\) are a bit more puzzling. Ostensibly, we have two different jobs to accomplish – we must scale them so that both of the edges that they will share with green triangles have the correct lengths. How do we know that this won’t require two different scaling factors? Conway also developed an elegant argument that handles this question as well. Consider the purple triangle at the bottom of the diagram in Figure \(9.1.3\)– it has vertex angles \((a,b,c^{\star\star})\). It is possible to construct triangles similar (via reflections) to the adjacent green triangles \((a, b^\star, c^\star)\) and \((a^\star, b, c^\star)\) of triangle \((a,b,c^{\star\star})\). To do this just construct two lines that go through the top vertex (where the angle \(c^{\star\star}\) is) that cut the opposite edge at the angle \(c^\star\) in the two possible senses – these two lines will coincide if it should happen that \(c^\star\) is precisely \(\dfrac{\pi}{2}\) but generally there will be two and it is evident that the two line segments formed have the same length. We scale the purple triangle so that this common length will be \(1\). See Figure \(9.1.4\).
If it should happen that \(c^{\star} = \dfrac{π}{2}\), what can we say about \(C\)?

Of course, the other two obtuse triangles can be handled in a similar way.
Exercises:
What value should we get if we sum all of the angles that appear around one of the interior vertices in the finished diagram? Verify that all three have the correct sum.
In this section, we talked about similarity. Two figures in the plane are similar if it is possible to turn one into the other by a sequence of mappings: a translation, a rotation and a scaling.
Geometric similarity is an equivalence relation. To fix our notation, let \(T(x, y)\) represent a generic translation, \(R(x, y)\) a rotation and \(S(x, y)\) a scaling – thus a generic similarity is a function from \(\mathbb{R}^2\) to \(\mathbb{R}^2\) that can be written in the form \(S(R(T(x, y)))\).
Discuss the three properties of an equivalence relation (reflexivity, symmetry and transitivity) in terms of geometric similarity.


