9.2: Five Steps Into the Void
- Page ID
- 19417
In this section we’ll talk about another Book proof also due to John Conway. This proof serves as an introduction to a really powerful general technique – the idea of an invariant. An invariant is some sort of quantity that one can calculate that itself doesn’t change as other things are changed. Of course different situations have different invariant quantities.
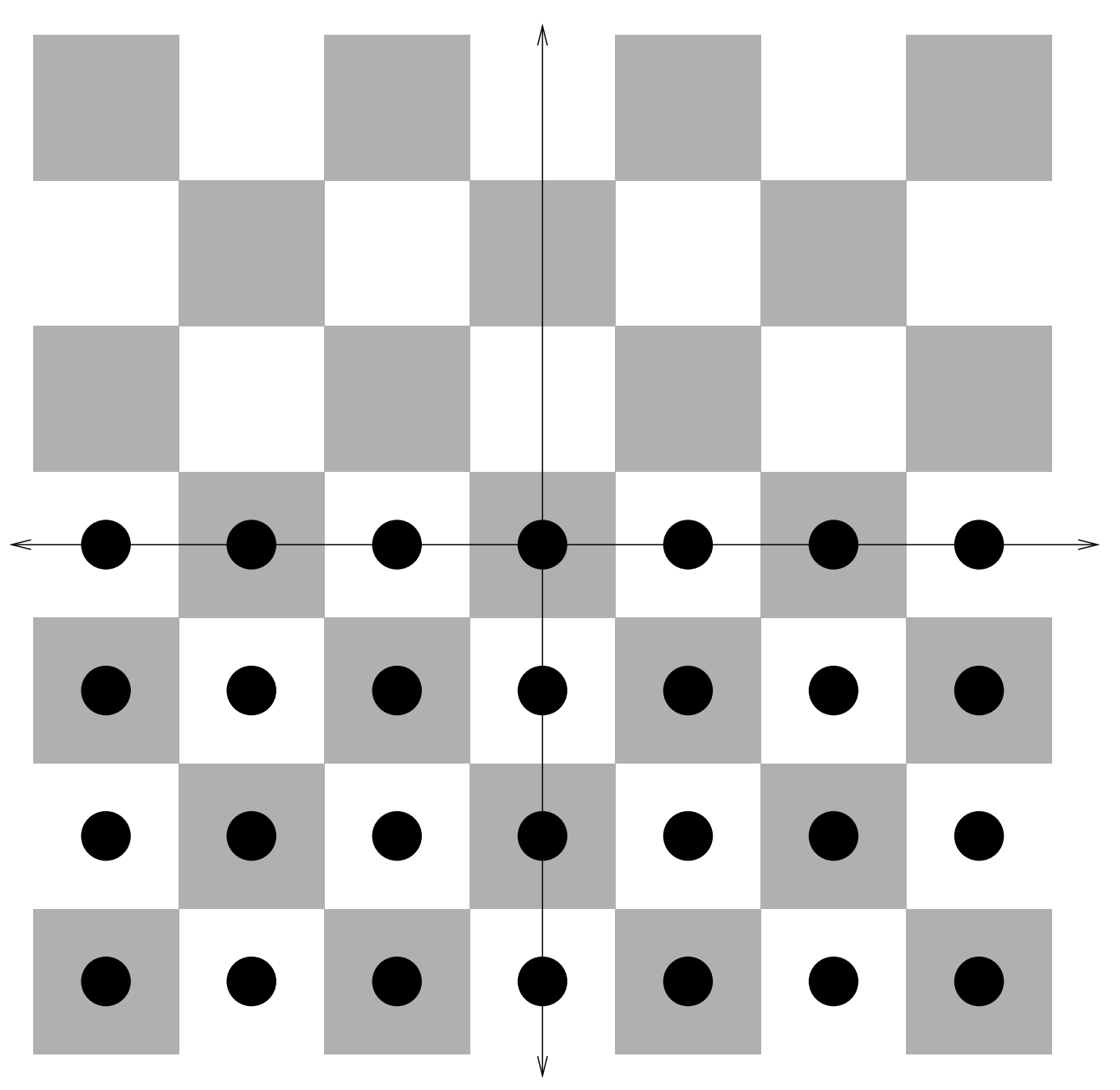
The setup here is simple and relatively intuitive. We have a bunch of checkers on a checkerboard – in fact we have an infinite number of checkers, but not filling up the whole board, they completely fill an infinite half-plane which we could take to be the set
\[ S = \{(x, y) x ∈ \mathbb{Z} ∧ y ∈ \mathbb{Z} ∧ y ≤ 0\}. \]
See Figure \(9.2.1\).
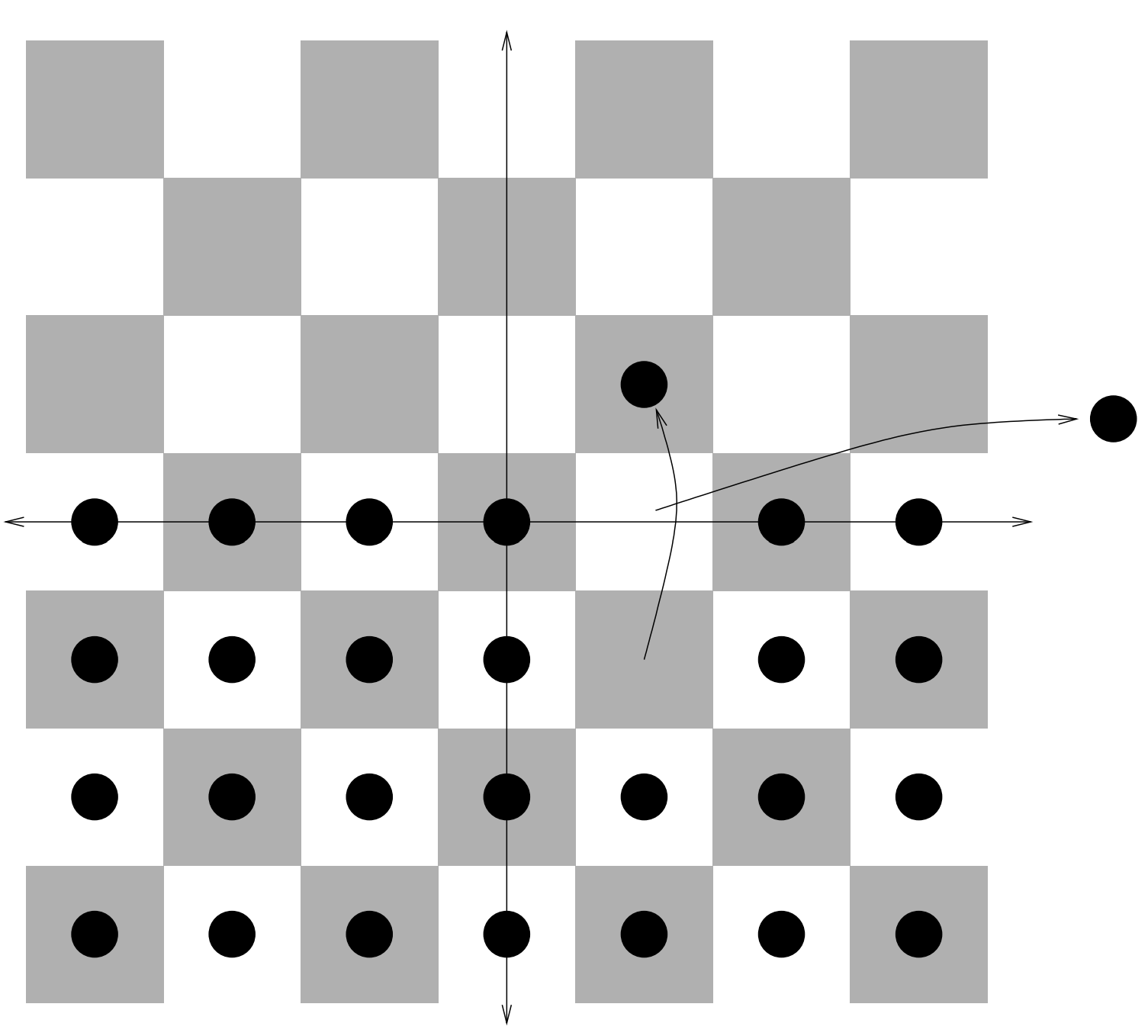
Think of these checkers as an army and the upper half-plane is “enemy territory.” Our goal is to move one of our soldiers into enemy territory as far as possible. The problem is that our “soldiers” move the way checkers do, by jumping over another man (who is then removed from the board). It’s clear that we can get someone into enemy territory – just take someone in the second row and jump a guy in the first row. It is also easy enough to see that it is possible to get a man two steps into enemy territory – we could bring two adjacent men a single step into enemy territory, have one of them jump the other and then a man from the front rank can jump over him.
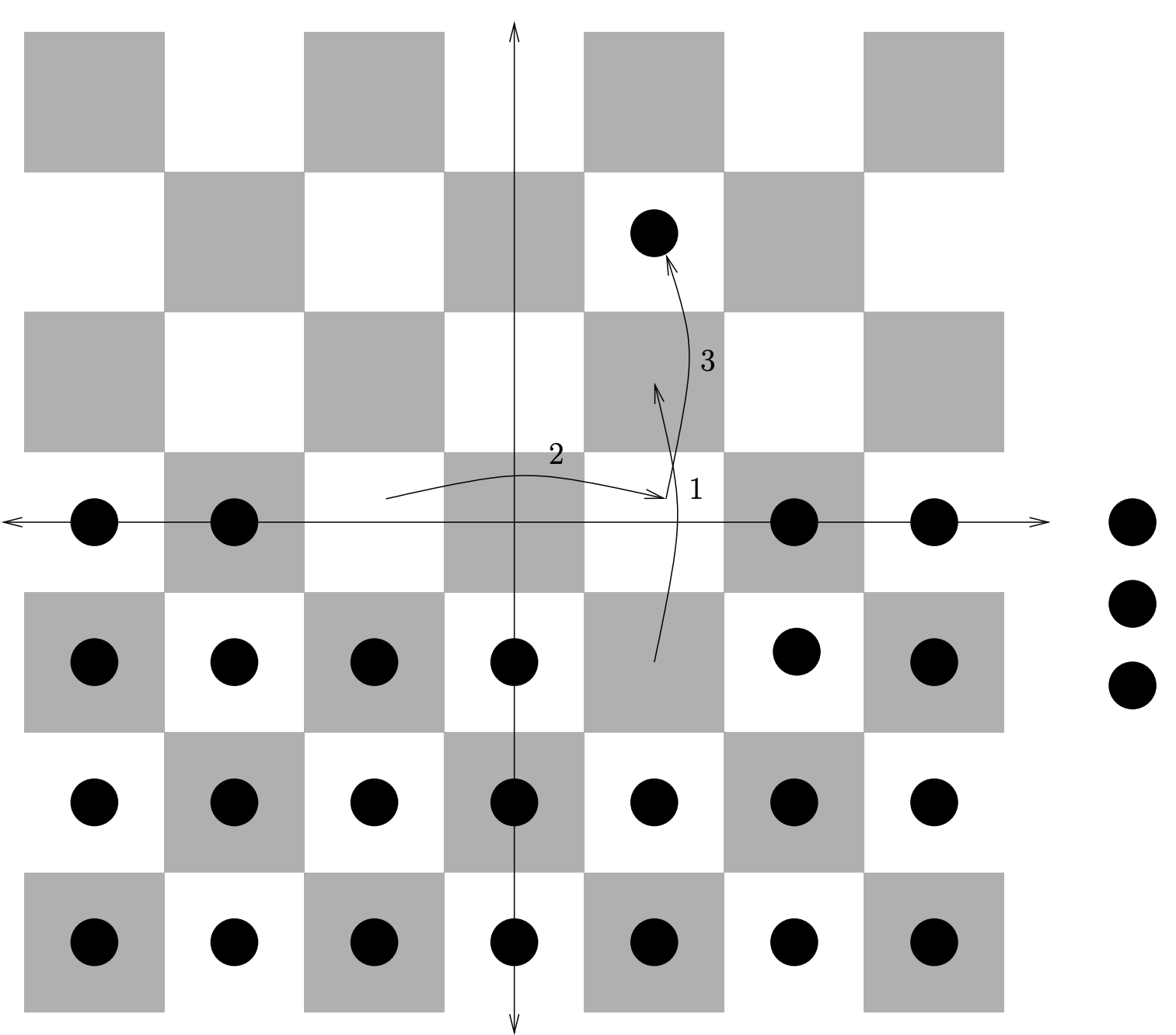
The strategy just stated uses \(4\) men (in the sense that they are removed from the board – \(5\) if you count the one who ends up two steps into enemy territory as well). Find a strategy for moving someone two steps into enemy territory that is more efficient – that is, involves fewer jumps.
Determine the most efficient way to get a man three steps into enemy territory. An actual checkers board and pieces (or some coins, or rocks) might come in handy.
We’ll count the man who ends up some number of steps above the \(x\)-axis, as well as all the pieces who get jumped and removed from the board as a measure of the efficiency of a strategy. If you did the last exercise correctly you should have found that eight men are the minimum required to get \(3\) steps into enemy territory. So far, the number of men required to get a given distance into enemy territory seems to always be a power of \(2\).
| # of steps | # of men |
| \(1\) | \(2\) |
| \(2\) | \(4\) |
| \(3\) | \(8\) |
As a picture is sometimes literally worth one thousand words, we include here \(3\) figures illustrating the moves necessary to put a scout \(1\), \(2\) and \(3\) steps into the void.
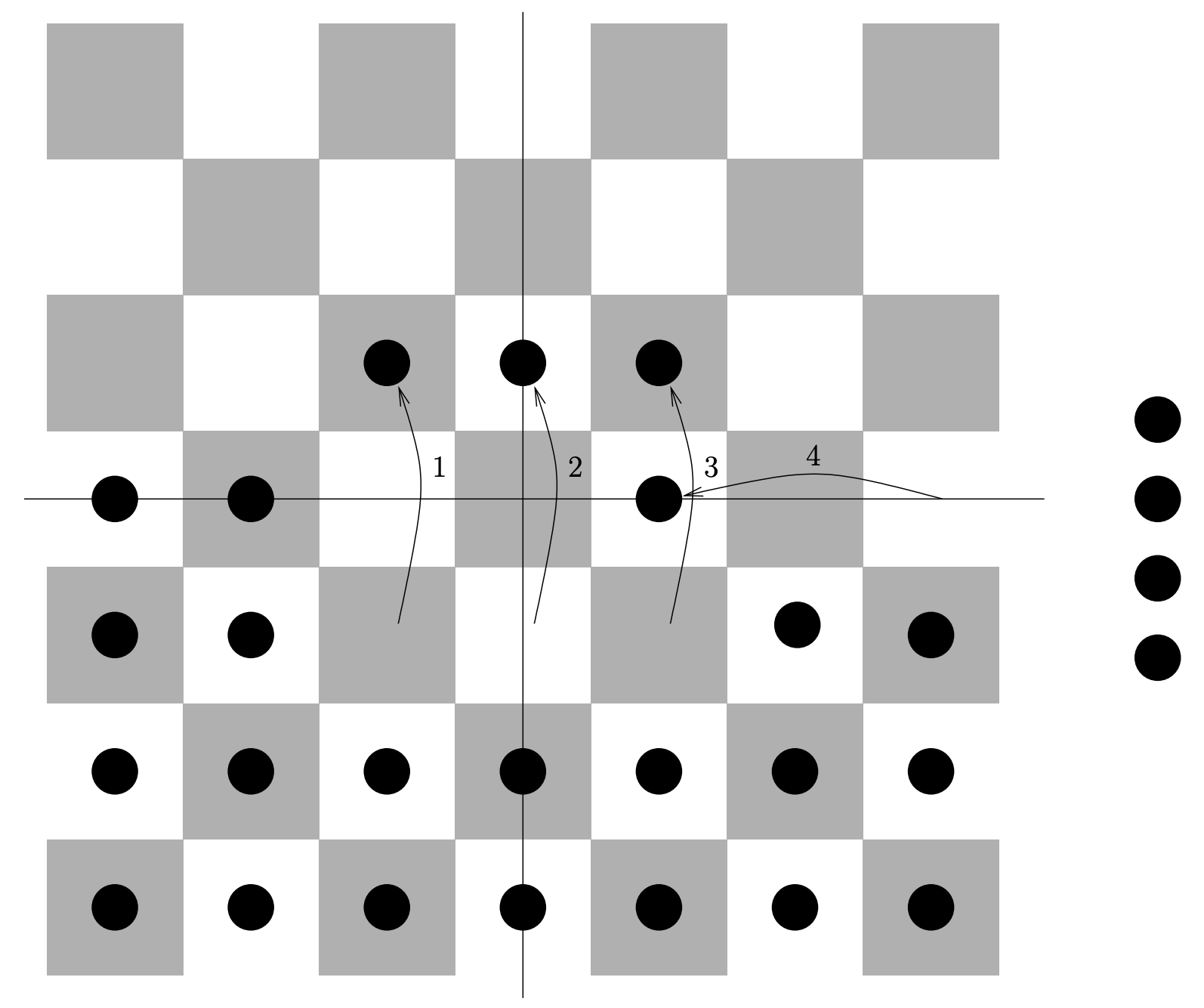
In order to show that \(8\) men are sufficient to get a scout \(3\) steps into enemy territory, we show that it is possible to reproduce the configuration that can place a man two steps in – shifted up by one unit.
You may be surprised to learn that the pattern of \(8\) men which are needed to get someone three steps into the void can be re-created – shifted up by one unit – using just \(12\) men. This means that we can get a man \(4\) steps into enemy territory using \(12 + 8 = 20\) men. You were expecting \(16\) weren’t you? (I know I was!)
The real surprise is that it is simply impossible to get a man five steps into enemy territory. So the sequence we’ve been looking at actually goes
\( 2, 4, 8, 20, \infty . \)
The proof of this surprising result works by using a fairly simple, but clever, strategy. We assign a numerical value to a set of men that is dependent on their positions – then we show that this value never increases when we make "checker jumping" moves – finally we note that the value assigned to a man in position \((0,5)\) is equal to the value of the entire original set of men (that is, with all the positions in the lower half-plane occupied). This is a pretty nice strategy, but how exactly are we going to assign these numerical values?
A man’s value is related to his distance from the point \((0,5)\) in what is often called "the taxicab metric." We don’t use the straight-line distance, but rather determine the number of blocks we will have to drive in the north-south direction and in the east-west direction and add them together. The value of a set of men is the sum of their individual values. Since we need to deal with the value of the set of men that completely fills the lower half-plane, we are going to have to have most of these values be pretty tiny! To put it in a more mature and dignified manner: the infinite sum of the values of the men in our army must be convergent.
We’ve previously seen geometric series which have convergent sums. Recall the formula for such a sum is
\[ \sum_{k=0}^{\infty} ar^k = \dfrac{a}{1-r}, \]
where \(a\) is the initial term of the sum and \(r\) is the common ratio between terms.
Conway’s big insight was to associate the powers of some number \(r\) with the positions on the board – \(r^k\) goes on the squares that are distance \(k\) from the target location. If we have a man who is actually at the target location, he will be worth \(r^0\) or \(1\). We need to arrange for two things to happen: the sum of all the powers of \(r\) in the initial setup of the board must be less than or equal to \(1\), and checker-jumping moves should result in the total value of a set of men going down or (at worst) staying the same. These goals push us in different directions: In order for the initial sum to be less than \(1\), we would like to choose \(r\) to be fairly small. In order to have checker-jumping moves we need to choose \(r\) to be (relatively) larger. Is there a value of \(r\) that does the trick? Can we find a balance between these competing desires?

Think about the change in the value of our invariant as a checker jumping move gets made. See Figure \(9.2.6\).
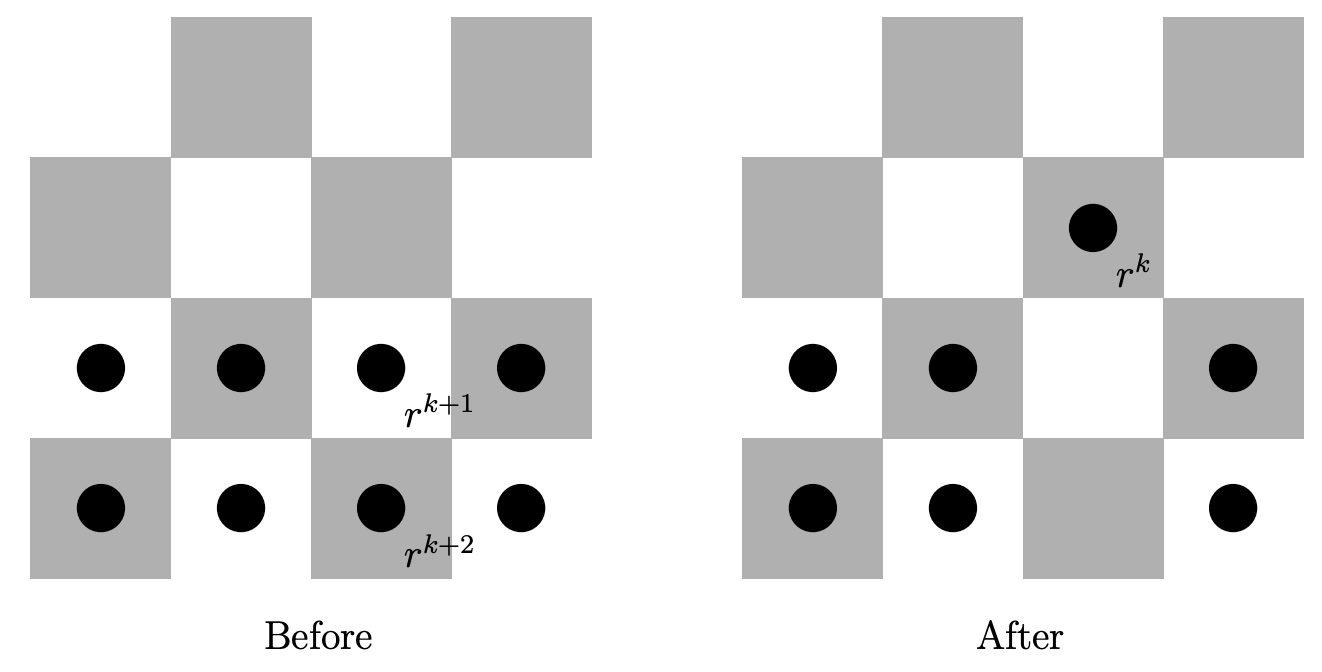
If we choose \(r\) so that \(r^{k+2} + r^{k+1} \; \leq \; r^k\) then the checker-jumping move will at worst leave the total sum fixed. Note that so long as \(r<1\) a checker-jumping move that takes us away from the target position will certainly decrease the total sum.
As is often the case, we’ll analyze the inequality by looking instead at the corresponding equality. What value of \(r\) makes \(r^{k+2} + r^{k+1} = r^k\)? The answer is that \(r\) must be a root of the quadratic equation \(x^2+x-1\).
Do the algebra to verify the previous assertion.
Find the value of \(r\) that solves the above equation.
Hopefully you used the quadratic formula to solve the previous exercise. You should of course have found two solutions, \(-1.618033989\ldots\) and \(.618033989\ldots\), these decimal approximations are actually \(-\phi\) and \(\dfrac{1}{\phi}\), where \(\displaystyle \phi = \frac{1+\sqrt{5}}{2}\) is the famous "golden ratio". If we are hoping for the sum over all the occupied positions of \(r^k\) to be convergent, we need \(|r|<1\), so the negative solution is extraneous and so the inequality \(r^{k+2} + r^{k+1} \; \leq \; r^k\) is true in the interval \([\dfrac{1}{\phi}, 1)\).
Next we want to look at the value of this invariant when "men" occupy all of the positions with \(y\leq0\). By looking at Figure \(9.2.5\) you can see that there is a single square with value \(r^5\), there are \(3\) squares with value \(r^6\), there are 5 squares with value \(r^7\), et cetera. The sum, \(S\), of the values of all the initially occupied positions is
\[ S = r^5 \sum_{k=0}^{\infty} (2k+1) r^k. \]
We have previously seen how to solve for the value of an infinite sum involving powers of \(r\). In the expression above we have powers of \(r\) but also multiplied by odd numbers. Can we solve something like this?
Let’s try the same trick that works for a geometric sum. Let
\[ T = \sum_{k=0}^{\infty} (2k+1) r^k = 1 + 3r + 5r^2 + 7r^3 + ... \]
Note that
\[ rT = \sum_{k=0}^{\infty} (2k+1) r^{k+1} = r + 3r^2 + 5r^3 + 7r^4 + ... \]
and it follows that
\[ T - rT = 1 + 2 \sum_{k=1}^{\infty} r^{k} = 1 + 2r + 2r^2 + 2r^3 + 2r^4 + ... \]
A bit more algebra (and the formula for the sum of a geometric series) leads us to
\[ T = \dfrac{1}{1-r} \left(1 + \dfrac{2r}{1-r} \right), \]
which simplifies to
\[ T = \dfrac{1+r}{1-r^2}. \]
Finally, recall that we are really interested in \(S = r^5 \cdot T\), or
\[ S = \dfrac{r^5 + r^6}{(1 − r)^2} . \]
It is interesting to proceed from this expression for \(S\), using the fact that \(r\) satisfies \(x^2 = 1 - x\), to obtain the somewhat amazing fact that \(S=1\).
The fact that \(S=1\) has an extraordinary consequence. In order to get a single checker to the position \((0,5)\) we would need to use everybody!
For a set consisting of just a single checker positioned at \((0,5)\) the value of our invariant is \(1\). On the other hand, the set consisting of the entire army lined up on and below the \(x\)-axis also yields a \(1\). Every checker move either does not change the value of the invariant or reduces it. The best we could possibly hope for is that there would be no need for moves of the sort that reduce the invariant – nevertheless we still could not get a man to \((0,5)\) in a finite number of moves.
Exercises:
Do the algebra (and show all your work!) to prove that invariant defined in this section actually has the value \(1\) for the set of all the men occupying the \(x\)-axis and the lower half-plane.
“Escape of the clones” is a nice puzzle, originally proposed by Maxim Kontsevich. The game is played on an infinite checkerboard restricted to the first quadrant – that is the squares may be identified with points having integer coordinates \((x, y)\) with \(x > 0\) and \(y > 0\). The “clones” are markers (checkers, coins, small rocks, whatever. . . ) that can move in only one fashion – if the squares immediately above and to the right of a clone are empty, then it can make a “clone move.” The clone moves one space up and a copy is placed in the cell one to the right. We begin with three clones occupying cells \((1, 1)\), \((2, 1)\) and \((1, 2)\) – we’ll refer to those three checkerboard squares as “the prison.” The question is this: can these three clones escape the prison?
You must either demonstrate a sequence of moves that frees all three clones or provide an argument that the task is impossible.


