1.5: Images and Inverses
- Page ID
- 101008
Functions can be used to define subsets of given sets.
Let \(f: X \rightarrow Y\) and \(W \subseteq X\). The image of \(W\) under \(f\), written \(f[W]\), is the set \[\{f(x) \mid x \in W\} .\] So if \(f: X \rightarrow Y\), then \[\operatorname{Ran}(f)=f[X] .\] EXAMPLE 1.30. Suppose \(f\) is the real function \(f(x)=x^{2}+3\). Let \(W=\{-2,2,3\}\), and \(Z=(-1,2)\). Then \(f[W]=\{7,12\}\), and \(f[Z]=[3,7)\).
In applications of mathematics, functions often describe numerical relationships between measurable observations. So if \(f: X \rightarrow Y\) and \(a \in X\), then \(f(a)\) is the predicted or actual measurement associated with \(a\). In this context, one is often interested in determining which elements of \(X\) are associated with a value, \(b\), in the codomain of \(f\).
Let \(f: X \rightarrow Y\) and \(b \in Y\). Then the inverse image of \(b\) under \(f, f^{-1}(b)\), is the set \[\{x \in X \mid f(x)=b\} .\] This set is also called the pre-image of \(b\) under \(f\).
Note that if \(b \notin \operatorname{Ran}(f)\), then \(f^{-1}(b)=\emptyset\). If \(f\) is an injection, then for any \(b \in \operatorname{Ran}(f), f^{-1}(b)\) has a single element.
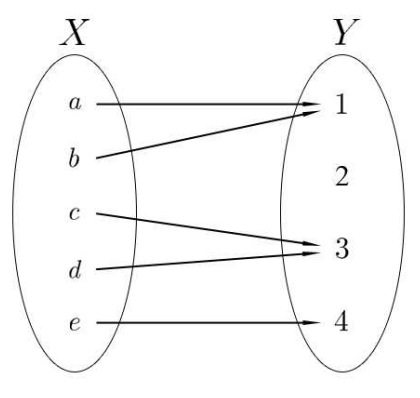
Let \(f: X \rightarrow Y\) and \(Z \subseteq Y\). The inverse image of \(Z\) under \(f\), or the pre-image of \(Z\) under \(f\), is the set \[f^{-1}[Z]=\{x \in X \quad \mid f(x) \in Z\}\] We use \(f^{-1}[]\) to mean the inverse image of a subset of the codomain, and \(f^{-1}\) ( ) for the inverse image of an element of the codomain - both are subsets of the domain of \(f\). If \(Z \cap \operatorname{Ran}(f)=\emptyset\), then \[f^{-1}[Z]=\emptyset .\] ExAMPLE 1.32. Let \(f\) be as in Figure \(1.33\) Then \(f[\{b, c\}]=\{1,3\}\), and \(f^{-1}[\{1,3\}]=\{a, b, c, d\}\).
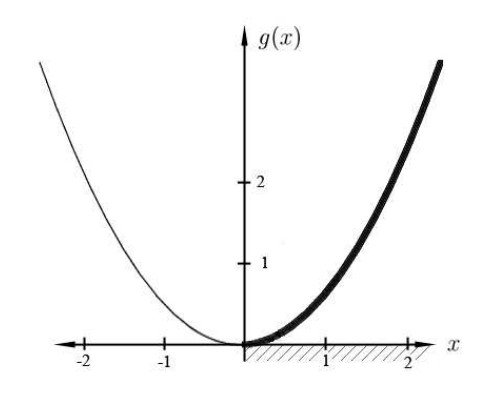
Let \(g\) be the real function \(g(x)=x^{2}+3\). If \(b \in \mathbb{R}\) and \(b>3\), then \[g^{-1}(b)=\{\sqrt{b-3},-\sqrt{b-3}\} .\] If \(b=3\), then \(g^{-1}(3)=\{0\}\). If \(b<3\), then \(g^{-1}(b)\) is empty.
Let \(h\) be the real function \(h(x)=e^{x}\). If \(b \in \mathbb{R}\) and \(b>0\), then \[h^{-1}(b)=\left\{\log _{e}(b)\right\} .\] For instance, \[h^{-1}(1)=\{0\} .\] Because \(h\) is strictly increasing, the inverse image of any element of the codomain \((\mathbb{R})\) is either a set with a single element or the empty set.
Let \(I=(a, b)\), where \(a, b \in \mathbb{R}\) and \(0<a<b\) (that is \(I\) is the open interval with end points \(a\) and \(b\) ). Then \[h^{-1}[I]=\left(\log _{e}(a), \log _{e}(b)\right) .\] We have discussed the construction of new functions from existing functions using algebraic operations and composition of functions. Another tool for building new functions from known functions is the inverse function.
Let \(f: X \mapsto Y\) be a bijection. Then the inverse function of \(f, f^{-1}: Y \rightarrow X\), is the function with graph \[\{(b, a) \in Y \times X \mid(a, b) \in \operatorname{graph}(f)\} .\] The function \(f^{-1}\) is defined by "reversing the arrows". For this to make sense, \(f: X \rightarrow Y\) must be bijective. Indeed, if \(f\) were not surjective, then there would be an element \(y\) of \(Y\) that is not in the range of \(f\), so cannot be mapped back to anything in \(X\). If \(f\) were not injective, there would be elements \(z\) of \(Y\) that were the image of distinct elements \(x_{1}\) and \(x_{2}\) in \(X\). One could not define \(f^{-1}(z)\) without specifying how to choose a particular pre-image. Both these problems can be fixed. If \(f\) is injective but not surjective, one can define \(g: X \mapsto \operatorname{Ran}(f)\) by \[g(x)=f(x)\] for all \(x \in X\). Then \(g^{-1}: \operatorname{Ran}(f) \mapsto X\). If \(f\) is not injective, the problem is trickier; but if we can find some subset of \(X\) on which \(f\) is injective, we could restrict our attention to that set.
Let \(f\) be the real function \(f(x)=x^{2}\). The function \(f\) is not an bijection, so it does not have an inverse function. However the function \[\begin{aligned} g:[0, \infty) & \rightarrow[0, \infty) \\ x & \mapsto x^{2} \end{aligned}\] is a bijection. In this case, \[g^{-1}(y)=\sqrt{y} .\]
Let \(f\) be the real function, \(f(x)=e^{x}\). You know from calculus that \(f\) is an injection, and that \(\operatorname{Ran}(f)=\mathbb{R}^{+}\). Hence \(f\) is not a surjection, since the implicit codomain of a real function is \(\mathbb{R}\). The function \[\begin{aligned} g: \mathbb{R} & \rightarrow \mathbb{R}^{+} \\ x & \mapsto e^{x} \end{aligned}\] is a bijection and \[g^{-1}(x)=\log _{e}(x)\] Warning: For \(f: X \mapsto Y\) a bijection we have assigned two different meanings to \(f^{-1}(b)\). In Definition 1.31, it means the set of points in \(X\) that get mapped to \(b\). In Definition 1.36, it means the inverse function, \(f^{-1}\), of the bijection \(f\) applied to the point \(b \in Y\). However, if \(f\) is a bijection, so that the second definition makes sense, then these definitions are closely related. Suppose \(a \in \operatorname{Dom}(f)\) and \(f(a)=b\). According to Definition 1.31, \(f^{-1}(b)=\{a\}\) and by Definition \(1.36\) \(f^{-1}(b)=a\). In practice the context will make clear which definition is intended. DEFINITION. Identity function, id \(\left.\right|_{X}\) Let \(X\) be a set. The identity function on \(X\), id \(\left.\right|_{X}: X \mapsto X\), is the function defined by \[\left.\operatorname{id}\right|_{X}(x)=x .\] If \(f: X \rightarrow Y\) is a bijection, then \(f^{-1}\) is the unique function such that \[f^{-1} \circ f=\left.\operatorname{id}\right|_{X}\] and \[f \circ f^{-1}=\left.\mathrm{id}\right|_{Y} .\] Because \(f(x)=x^{2}\) is not an injection, it has no inverse, even after restricting the codomain to be the range. Therefore in order to "invert" \(f\), we considered a different function \(g(x)\), which was equal to \(f\) on a subset of the domain of \(f\), and was an injection. In Example 1.37, we accomplished this by defining the function \(g(x)=x^{2}\) with domain \(\{x \in \mathbb{R} \mid x \geq 0\}\). Many of the functions that we need to invert for practical and theoretical reasons happen not to be injections, and hence do not have inverse functions. One way to address this obstacle is to consider the function on a smaller domain.
Given a function, \(f: X \rightarrow Y\) we may wish to define an "inverse" of \(f\) on some subset of \(W \subseteq X\) for which the restriction of \(f\) to \(W\) is an injection.
Let \(f: X \rightarrow Y\) and \(W \subseteq X\). The restriction of \(f\) to \(W\), written \(\left.f\right|_{W}\), is the function \[\begin{aligned} \left.f\right|_{W}: W & \rightarrow Y \\ x & \mapsto f(x) . \end{aligned}\] So if \(f: X \rightarrow Y\) and \(W \subseteq X\), then \[\operatorname{graph}\left(\left.f\right|_{W}\right)=[W \times Y] \cap[\operatorname{graph}(f)] .\] EXAMPLE 1.40. Let \(f(x)=(x-2)^{4}\). Let \(W=[2, \infty)\). Then \[\left.f\right|_{W}: W \rightarrow[0, \infty)\] is a bijection. ExAmPLE 1.41. Let \(f\) be the real function, \(f(x)=\tan (x)\). Then \[\operatorname{Dom}(f)=\{x \in \mathbb{R} \mid x \neq \pi / 2+k \pi, k \in \mathbb{Z}\},\] and \[\operatorname{Ran}(f)=\mathbb{R} .\] The function \(f\) is periodic with period \(\pi\), and is therefore not an injection. Nonetheless, it is important to answer the question, "At what angle(s), \(x\), does \(\tan (x)\) equal a particular value, \(a \in \mathbb{R}\) ".
This is mathematically equivalent to asking, \[\text { "What is } \arctan (a) \text { ?". }\] In calculus this need was met by restricting the domain to a largest interval, \(I\) such that \[\left.f\right|_{I}: I \mapsto \mathbb{R}\] For any \(k \in \mathbb{Z}\), \[\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\] is such an interval. In order to define a specific function, the simplest of these intervals is selected, and we define \[\operatorname{Tan}:=\left.\tan \right|_{(-\pi / 2, \pi / 2)} .\] Observe that \[\text { Tan : }(-\pi / 2, \pi / 2) \mapsto \mathbb{R} .\] So the function is invertible, that is, Tan has an inverse function, \[\operatorname{Arctan}=\operatorname{Tan}^{-1} \text {. }\]


