2.4: Constructing Bijections
- Page ID
- 99059
Let’s consider a particularly interesting and important abstract application of equivalence classes. Let \(f: X \rightarrow Y\). The function \(f\) need not be an injection or surjection. However, we have already discussed the desirability of finding an "inverse" for \(f\), even when it fails to meet the necessary conditions for the existence of an inverse. In Section \(1.3\) we considered the function \(\left.f\right|_{D}\), where \(D \subseteq X\) and \(\left.f\right|_{D}\) is an injection. Another approach is to use the function \(f\) to create a new function on a distinct domain that preserves much of the information of \(f\).
We use \(f\) to induce an equivalence relation on \(X\). Define a relation \(\sim\) on \(X\) by \[x \sim y \text { if and only if } f(x)=f(y) .\] We showed in Example \(2.18\) that \(\sim\) is an equivalence relation; it is the equivalence relation on \(X\) induced by \(f\). The equivalence relation \(\sim\) induces a partition of \(X\), namely \(X / \sim(\) which is the set \(\{[x] \mid x \in X\}\) of all equivalence classes). Notation. \(X / f\) Let \(f: X \rightarrow Y\) and \(\sim\) be the equivalence relation on \(X\) induced by \(f\). We write \(X / f\) for the set of equivalence classes induced by \(\sim\) on \(X\).
An equivalence class in \(X / f\) is the inverse image of an element in \(\operatorname{Ran}(f)\). That is, if \(x \in X\) and \(f(x)=y\), \[[x]=f^{-1}(y) .\] So \[X / f=\left\{f^{-1}(y) \mid y \in \operatorname{Ran}(f)\right\} .\] The elements of \(X / f\) are called the level sets of \(f\). The inspiration for this comes from thinking of a topographical map. The curves on a topographical map corresponding to fixed altitudes are called level curves. Consider the function from a point on a map to the altitude of the physical location represented by the point on the map. Level curves on the map are subsets of the level sets of this function.
Notation. \(\Pi_{f}\) Let \(f: X \rightarrow Y\). The function \(\Pi_{f}: X \rightarrow X / f\) is defined by \(\Pi_{f}(x)=[x]_{f}\), where \([x]_{f}\) is the equivalence class of \(x\) with respect to the equivalence relation induced by \(f\).
Let \(Z \subseteq Y\) be the range of \(f\). We define a new function, \(\widehat{f}: X / f \rightarrow Z\) by \[\widehat{f}([x])=f(x) .\] The function \(\widehat{f}\) is closely related to \(f\); in fact, for every \(x \in X\), \[f(x)=\widehat{f} \circ \Pi_{f}(x) .\] This is sometimes illustrated with a diagram, as in Figure \(2.22\).
The function \(\hat{f}\) is a bijection. In this sense, every function can be canonically associated with a bijection. We consider the function that we looked at in Section 1.3.
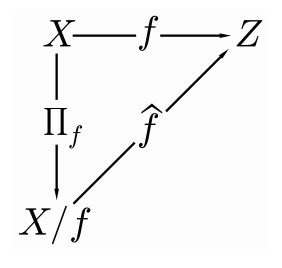
Let \(f(x)=\tan (x)\). As we discussed earlier, we can "invert" this function by considering the function Tan : \((-\pi / 2, \pi / 2) \rightarrow\) \(\mathbb{R}\) by \[\operatorname{Tan}=\left.\tan \right|_{(-\pi / 2, \pi / 2)}\] The function Tan is a bijection, and has an inverse, \[\operatorname{Arctan}: \mathbb{R} \rightarrow(-\pi / 2, \pi / 2)\] For any \(k \in \mathbb{Z}\) there is a corresponding restriction of tan, \[\tan \mid\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\] which is a bijection, and therefore has an inverse function.
Another bijection can be constructed on the equivalence classes induced by \(f(x)=\tan (x)\). A level set of \(f\) is \([x]_{f}=\{x+k \pi \mid k \in \mathbb{Z}\}\). Let \(X\) be the domain of tan. Then \[X / f=\left\{[x]_{f} \mid x \in X\right\}\] We can interpret an equivalence class \([x]_{f}\) with respect to angles in standard position in the Cartesian plane. The equivalence class of \(x\) is the set of angles in standard position that have terminal side collinear with the terminal side of the angle \(x\) - see Figure 2.24.
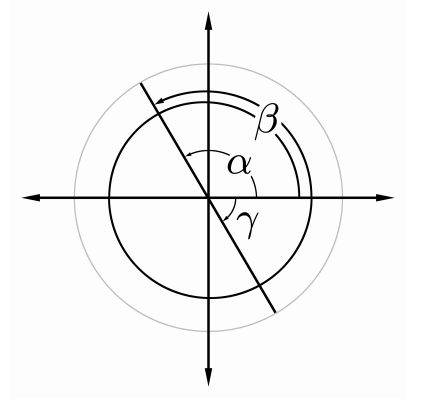
Following the construction outlined above, the function \(\Pi_{f}: X \rightarrow\) \(X / f\) is the function \[\Pi_{f}(x)=[x]_{f}=\{x+k \pi \mid k \in \mathbb{Z}\} .\] The function \(\widehat{f}: X / f \rightarrow \mathbb{R}\) given by \[\widehat{f}\left([x]_{f}\right)=f(x)\] is a bijection. Furthermore, \[\tan =\widehat{f} \circ \Pi_{f} .\] If \(x \in X\), then \(\Pi_{f}(x)\) is the set of all angles that have terminal side collinear with the terminal side of angle \(x\) in standard position. Thus \(\Pi_{f}\) tells us that \(\tan\) can distinguish only the slope of the terminal side of the angle - not the quadrant of the angle or how many revolutions the angle subtended.


