6.1: Cardinality

In this chapter we use functions to explore the idea of the size of a set. The results we derive are deep and very interesting, especially when we consider the simplicity of the tools we are using. Of course, we shall have to use these tools somewhat cleverly.

Set theory comes in different flavors. The most difficult is axiomatic set theory. Many interesting results have been derived in formal axiomatic set theory, but the topic is advanced and not suitable for an introduction to higher mathematics. Instead, we shall study what is called naive set theory. The use of the word "naive" is not pejorative, but is meant to differentiate this approach from axiomatic set theory. Most mathematicians have studied naive set theory, but relatively few have worked extensively with set axioms.

Cardinality

We wish to compare the size of sets. The fundamental tool for our investigation is the bijection. In the case of finite sets, which can be exhaustively listed, this is easy. Given any two finite sets, \(X\) and \(Y\), we could list the elements and count them. Provided that our lists have no redundancies, the larger set is the one with the higher count. The act of listing the elements in a set, where this is possible, is also defining a bijection from a natural number (interpreted as a set) to the set being counted. The idea of using functions to compare the size of sets can be generalized to arbitrary sets.

When it comes to comparing the size of infinite sets there are competing intuitions. On the one hand we have an intuition that if one set is a proper subset of another set, it should be smaller. On the other hand if two sets are infinite, how can one be larger than the other? Using bijections, injections and surjections to define the relative size of sets allows us to see our way through this paradox.

Definition. Equinumerous, cardinality Let \(X\) and \(Y\) be sets. We say that \(X\) and \(Y\) have the same cardinality if there is a bijection \(f: X \mapsto Y\). We can express that two sets have the same cardinality by \[|X|=|Y| .\] If \(|X|=|Y|\), then we say that \(X\) and \(Y\) are equinumerous.

CLAIM. Equinumerosity is an equivalence relation.

(Prove this: Exercise 6.2).

Although we used the ideas of finite and infinite before now, we shall define the ideas in terms of bijections.

DEFINITION. Finite, infinite Let \(X\) be a set. \(X\) is finite if there exists some \(n \in \mathbb{N}\) and a bijection \(f:\ulcorner n\urcorner \mapsto X\). In the case that \(X=\emptyset\), we say that \(X\) is bijective with \(\ulcorner 0\urcorner\) via the empty function. If \(X\) is not finite, we say that \(X\) is infinite.

So a set is finite if it is bijective with a set \(\ulcorner n\urcorner\) for some \(n \in \mathbb{N}\). It is probably no surprise that a set cannot be bijective with different natural numbers.

PROPOSITION 6.1. Let \(m, n \in \mathbb{N}\). Then \[(|\ulcorner m\urcorner|=|\ulcorner n\urcorner|) \Longleftrightarrow(m=n) .\] Discussion. We prove the non-trivial direction of this biconditional by induction on one of the integers in the statement.

PROOF. \(\Leftarrow\)

Let \(m=n\). Then it is obvious that \[|\ulcorner m\urcorner|=|\ulcorner n\urcorner| .\] \(\Rightarrow\)

We argue by induction on \(m\).

Base case:

If \(m=0\) and \(\left|\left\ulcorner^{n}\right\urcorner\right|=\mid\left\ulcorner_{m}||\right.\) then clearly \(n=0\).

Induction step:

Let \(m \in \mathbb{N}\) and assume that \[(\forall n \in \mathbb{N})\left[\left|\left\ulcorner^{\prime}\right\urcorner\right|=|\ulcorner\urcorner|\right] \Rightarrow[m=n]\] We show that \[(\forall n \in \mathbb{N})[|\ulcorner m+1\urcorner|=|\ulcorner n\urcorner|] \Rightarrow[m+1=n]\] Assume that \[\left|\left\ulcorner^{m}+1\right\urcorner\right|=\left|\left\ulcorner^{\urcorner} n\right\rangle\right|\] Let \[f:\ulcorner m+1\urcorner \longmapsto\ulcorner n\urcorner\] DiscuSsion. A natural way to proceed with this argument is to restrict the domain of \(f\) to \(\ulcorner m\urcorner\) and use the induction hypothesis. Unfortunately if \(f(m) \neq n-1\) then \(\left.\left.f\right|_{\ulcorner m}\right\urcorner\) is not a bijection from \(\ulcorner m\urcorner\) to \(\ulcorner n-1\urcorner\), and the induction hypothesis will not directly apply. To address this issue, we shall define a permutation \(g:\ulcorner m+1\urcorner \rightarrow\ulcorner m+1\urcorner\) that rearranges the elements of \(\ulcorner m+1\urcorner\) so that \(f \circ g\) will be a bijection satisfying \[(f \circ g)(m)=n-1\] We define \(g:\ulcorner m+1\urcorner \rightarrow\ulcorner m+1\urcorner\) as follows: \[g(x)=\left\{\begin{array}{clc} f^{-1}(n-1) & \text { if } & x=m \\ m & \text { if } \quad x=f^{-1}(n-1) \\ x & & \text { otherwise. } \end{array}\right.\] Let \(h=f \circ g\). Then \(h\) is a bijection and \[h(m)=(f \circ g)(m)=n-1\]

FIGURE 6.2. Picture of the permutation \(g\)

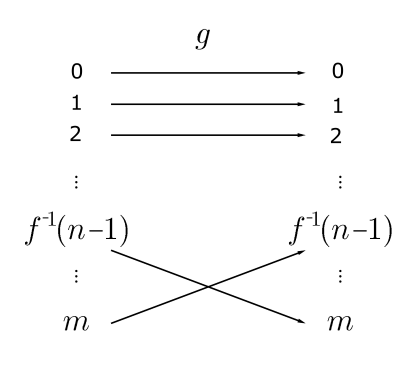
Therefore \[\left.h\right|_{\left\ulcorner_{m}\right\urcorner}:\ulcorner m\urcorner \mapsto\ulcorner n-1\urcorner .\] By the induction hypothesis \[m=n-1 .\] Therefore \[m+1=n .\] By the induction principle, \[(\forall m \in \mathbb{N})(\forall n \in \mathbb{N})(|\ulcorner m\urcorner|=|\ulcorner n\urcorner|) \Rightarrow(m=n) .\] COROLLARY 6.3. If \(X\) is a finite set, there is exactly one \(n \in \mathbb{N}\) such that \(\ulcorner n\urcorner\) is bijective with \(X\).

Discussion. This is a standard uniqueness argument. We assume that a set is bijective with natural numbers \(\ulcorner n\urcorner\) and \(\ulcorner m\urcorner\), and we use that the composition of bijections is a bijection to show that \(m=n\). This is not a proof by contradiction. Rather we are proving that any two names for natural numbers that are bijective with \(X\) must name the same natural number. Proof. \(X\) is finite, so there is \(n \in \mathbb{N}\) such that \[|X|=|\ulcorner n\urcorner| .\] Let \(m \in \mathbb{N}\) and \[|X|=|\ulcorner m\urcorner| .\] Let \(f: X \mapsto\ulcorner n\urcorner\) and \(g: X \mapsto\ulcorner m\urcorner\). Then \(g^{-1}:\ulcorner m\urcorner \mapsto X\). The composition of bijections is a bijection, so \[f \circ g^{-1}:\ulcorner m\urcorner \mapsto\ulcorner n\urcorner .\] By Proposition 6.1, \[m=n .\] DEFINITION. Finite cardinality If \(X\) is a finite set, we say that it has finite cardinality. Let \(n \in \mathbb{N}\) be the unique natural number such that \(\ulcorner n\urcorner\) is bijective with \(X\). Then we say that \(X\) has cardinality \(n\), or \[|X|=n \text {. }\] Corollary \(6.3\) guarantees that the cardinality of a finite set is welldefined.