6.4: Countable Sets

The uncountable sets we have identified so far have a certain structural characteristic in common. We have shown that the set of all functions from a fixed infinite domain to a fixed codomain of at least two elements is uncountable. Cantor’s theorem that the power set of an infinite countable set is uncountable can be interpreted this way as well. If \(X\) is a set, then \(P(X)\) can be understood as \(\ulcorner 2\urcorner X\), the set of all functions from \(X\) to \(\ulcorner 2\urcorner\). In the case of finite sets, \(X\) and \(Y\), the set of all functions from \(X\) to \(Y, Y^{X}\), has cardinality \(|Y|^{|X|}\). That is, the cardinality of \[\{f \subseteq X \times Y \mid f \text { is a function }\}\] is an exponential function of \(|X|\). Of course, exponential functions grow relatively fast. For finite sets, the cardinality of the union of disjoint sets is the sum of the cardinalities of the sets. The cardinality of the direct product of two finite sets is the product of the cardinalities. What happens to the union or the direct product of countable infinite sets? Can the set operations of union and direct product generate uncountable sets from countable sets? We answer the questions for unions (addition) first.

The following proposition will simplify some of the technical details in the arguments which follow.

PROPOSITION 6.15. Let \(X\) and \(Y\) be sets. Then there is a surjection \(f: X \rightarrow Y\) iff \(|Y| \leq|X| .\)

Discussion. We shall use the level sets of the surjection \(f\) to define the injection from \(Y\) to \(X\). This uses the machinery of equivalence relations developed in Chapter 2 with the Axiom of Choice.

Proof. \((\Rightarrow)\)

Let \(X, Y\) and \(f\) be as in the statement of the proposition. Let \[\widehat{f}: X / f \rightarrow Y\] be the canonical bijection associated with \(f\) that was defined in Section 2.3. We ask whether there is an injection \(g: X / f \rightarrow X\) where \(g([x]) \in[x]\). Recall that \(X / f\) is the collection of level subsets of \(X\), with respect to \(f\), and is a partition of \(X\). Why not simply choose an element from each equivalence class and define \(g\) to be the function from \(X / f\) to \(X\) defined by these choices?

DISCUSSION. The Axiom of Choice is the assertion that such "choice" functions exist.

The function \(g\) is clearly an injection, so \[g \circ \widehat{f}^{-1}: Y \rightarrow X\] is an injection. Therefore if there is a surjection \(f: X \rightarrow Y\), then \(|Y| \leq|X|\).

\((\Leftarrow)\)

The proof of this implication is left as an exercise.

THEOREM 6.16. Cantor’s Theorem Let \(\left\{X_{n} \mid n \in \mathbb{N}\right\}\) be a family of sets such that \(X_{n}\) is countable for all \(n \in \mathbb{N}\), and \(X=\bigcup_{n \in \mathbb{N}} X_{n}\). Then \[|X| \leq \aleph_{0}\] Discussion. This Theorem, also due to G. Cantor, is the key result for proving that sets are countable. It is proved by a technique also called a diagonal argument (sometimes called the first diagonal argument). We use the index set \(\mathbb{N}\) to construct an infinite array, and use that array to illustrate an enumeration of the union. This enumeration is a surjection from \(\mathbb{N}\) to \(X\).

PROOF. For \(n \in \mathbb{N}, X_{n}\) is countable and by Proposition \(6.15\) there is a surjection \[f_{n}: \mathbb{N} \rightarrow X_{n}\] Use the functions \(f_{n}\) to construct an infinite array. The \(0^{\text {th }}\) column will contain all the elements of \(X_{0}\), in the order \(f_{0}(0), f_{0}(1), f_{0}(2), \ldots\) (It does not matter if the same element is listed multiple times). The next column has the elements of \(X_{1}\) in the order \(f_{1}(0), f_{1}(1), f_{1}(2)\), etc. We define a function \(g: \mathbb{N} \rightarrow X\) by traversing this array along the northeast to southwest diagonals, viz. \(g(0)=f_{0}(0), g(1)=f_{1}(0), g(2)=\) \(f_{0}(1), g(3)=f_{2}(0), g(4)=f_{1}(1), g(5)=f_{0}(2), g(6)=f_{3}(0)\), and so on.

FIGURE 6.17. The first diagonal argument

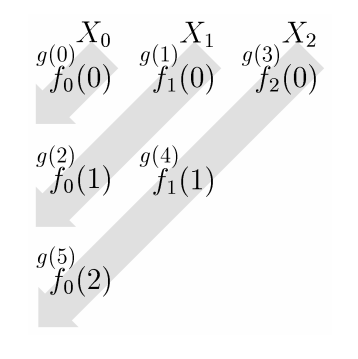
Then \(g\) is a surjection, because every element of \(\bigcup X_{n}\) occurs in the array, and is therefore in the range of \(g\). By Proposition 6.15, \[|X| \leq \aleph_{0} .\] COROLLARY 6.18. Let \(A\) be a countable set and \(\left\{X_{\alpha} \mid \alpha \in A\right\}\) be a family of countable sets indexed by A. Then \[\left|\bigcup_{\alpha \in A} X_{\alpha}\right| \leq \aleph_{0} \text {. }\] Proof. Since \(A\) is countable, there is a surjection \[f: \mathbb{N} \rightarrow A .\] Therefore \[\bigcup_{\alpha \in A} X_{\alpha}=\bigcup_{n \in \mathbb{N}} X_{f(n)}\] By Cantor’s Theorem 6.16, \[\left|\bigcup_{\alpha \in A} X_{\alpha}\right| \leq \aleph_{0} .\] COROLLARY 6.19. \(\mathbb{Z}\) is countable.

Discussion. Without too much effort, we could define a bijection from \(\mathbb{N}\) to \(\mathbb{Z}\). Instead we shall prove the existence of the bijection without explicitly defining a bijection.

Proof. Let \(f: \mathbb{N} \rightarrow \mathbb{Z}\) be such that \[f(n)=-n .\] Then \(f[\mathbb{N}]\) is countable. By Cantor’s Theorem \[\mathbb{Z}=\mathbb{N} \cup f[\mathbb{N}]\] is countable.

We turn our attention to direct products.

THEOREM 6.20. If \(n \in \mathbb{N}\), and \(X_{1}, X_{2}, \ldots, X_{n}\) are countable sets, then \[X_{1} \times X_{2} \times \cdots X_{n}\] is countable.

Proof. We assume that all of the factors, \(X_{1}, \ldots, X_{n}\) are nonempty. We argue by induction on the number of factors.

Base case: \(n=2\). \[X_{1} \times X_{2}=\bigcup_{x \in X_{2}} X_{1} \times\{x\}\] For each \(x \in X_{2}\), \[\left|X_{1}\right|=\left|X_{1} \times\{x\}\right| .\] By Corollary 6.18, \(X_{1} \times X_{2}\) is countable.

Induction step: Assume that for any collection of \(n\) countable sets \(X_{1}, \ldots X_{n}\), the product \(X_{1} \times \cdots \times X_{n}\) is countable. Let \(X_{1}, \ldots, X_{n+1}\) be countable nonempty sets. Then \[X_{1} \times \cdots \times X_{n+1}=\left(X_{1} \times \cdots \times X_{n}\right) \times X_{n+1}\] By the induction hypothesis, \(X_{1} \times \cdots \times X_{n}\) is countable, and by the base case the direct product of two countable sets is countable. Therefore, \(X_{1} \times \cdots \times X_{n+1}\) is countable.

COROLLARY 6.21. \(\mathbb{Q}\) is countable.

Proof. Let \(f: \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Q}\) be defined by \[f(a, b)=\left\{\begin{array}{ccc} a / b & \text { if } & b \neq 0 \\ 0 & \text { otherwise. } \end{array}\right.\] Then \(f\) is a surjection, and by Proposition \(6.15, \mathbb{Q}\) is countable.

We have evaluated the nested sequence of sets, \[\mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q} \subsetneq \mathbb{R} \text {. }\] These are important mathematical sets and, with the exception of \(\mathbb{R}\), they are countable. We investigate the cardinality of one more set between \(\mathbb{Q}\) and \(\mathbb{R}\).

DEFINITION. Algebraic real number, \(\mathbb{K}\) A real number \(\alpha\) is algebraic if there is a polynomial \(p\) (not identically 0 ) with integer coefficients such that \(p(\alpha)=0\). We shall denote the set of all algebraic numbers by \(\mathbb{K}\).

Any rational number \(a / b \in \mathbb{Q}\) is algebraic, since \(a / b\) is a root of the polynomial \[p(x)=b x-a .\] Moreover, in Example 3.23, we showed that \(\sqrt{2}\) is irrational, and it is clearly algebraic, since it is a root of \(x^{2}-2\). Therefore we have \[\mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q} \subsetneq \mathbb{K} \subseteq \mathbb{R} .\] Finally we prove that \(\mathbb{K} \neq \mathbb{R}\) by showing that \(\mathbb{K}\) is countable. THEOREM 6.22. \(\mathbb{K}\) is countable.

Discussion. This result is proved by showing that the algebraic real numbers can be constructed by a countable procedure. That is, \(\mathbb{K}\) may be built by adding to \(\mathbb{Q}\) countably many elements at a time countably many times. Cantor’s Theorem implies that any set so constructed will be countable.

PROOF. Let \(n \in \mathbb{N}\) and define \(f: \prod_{i=0}^{n} \mathbb{Z} \rightarrow \mathbb{Z}[x]\) by \[f\left(a_{0}, \ldots, a_{n}\right)=\sum_{i=0}^{n} a_{i} x^{i} .\] By Corollary 6.19, \(\mathbb{Z}\) is countable. By Theorem 6.20, \(\prod_{i=0}^{n} \mathbb{Z}\) is countable. The range of \(f\) is the set of polynomials with integer coefficients with degree \(\leq n\) (or the polynomial identically equal to 0 ). By Proposition \(6.15\), the range of a function with a countable domain is countable as well. Therefore the set of polynomials of degree \(\leq n\) is countable.

Let \(P_{n}\) be the set of polynomials with integer coefficients of degree \(\leq n\). Then \[\mathbb{Z}[x]=\bigcup_{i=0}^{\infty} P_{n} .\] By Theorem 6.16, \(\mathbb{Z}[x]\) is countable. By Theorem 4.10, if \(p(x)\) is a polynomial with real coefficients of degree \(n\), it has at most \(n\) real roots. Let \[Z_{p}=\{\alpha \mid p(\alpha)=0\} .\] So \(Z_{p}\) is finite for every polynomial \(p\). Applying Cantor’s Theorem (Theorem 6.16) again, \[\mathbb{K}=\bigcup_{p \in \mathbb{Z}[x]} Z_{p}\] is countable.

COROLLARY 6.23. \(\mathbb{K} \neq \mathbb{R}\)

Since \(\mathbb{K}\) is countable and \(\mathbb{R}\) is uncountable, \(\mathbb{K}\) is a proper subset of \(\mathbb{R}\). DEFINITION. Transcendental number A real number that is not algebraic is called a transcendental number.

Corollary \(6.23\) states that there are transcendental numbers. This is an existence claim in which no witness to the claim is produced. Rather it is an example of a counting argument (on infinite sets). There are too many real numbers for them all to be algebraic. By the end of the nineteenth century it was proved that \(\pi\) and \(e\) are transcendental, but these proofs are much more complicated than Cantor’s existence proof above, which is, in essence, a very clever application of the pigeon-hole principle.

COROLLARY 6.24. There are uncountably many transcendental numbers.

PROOF. Let \(T\) be the set of transcendental numbers. As \[|\mathbb{R}|=|T \cup \mathbb{K}|>\aleph_{0},\] and \(\mathbb{K}\) is countable, \(T\) must be uncountable.

So we have shown that \[\mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q} \subsetneq \mathbb{K} \subsetneq \mathbb{R} .\] However, \[|\mathbb{N}|=|\mathbb{Z}|=|\mathbb{Q}|=|\mathbb{K}|<|\mathbb{R}|\]