8.1: Solve Equations Using the Subtraction and Addition Properties of Equality (Part 1)
- Page ID
- 5019
- Solve equations using the Subtraction and Addition Properties of Equality
- Solve equations that need to be simplified
- Translate an equation and solve
- Translate and solve applications
Before you get started, take this readiness quiz.
- Solve: n − 12 = 16. If you missed this problem, review Example 2.5.6.
- Translate into algebra ‘five less than x.’ If you missed this problem, review Example 2.4.12.
- Is x = 2 a solution to 5x − 3 = 7? If you missed this problem, review Example 2.5.1.
We are now ready to “get to the good stuff.” You have the basics down and are ready to begin one of the most important topics in algebra: solving equations. The applications are limitless and extend to all careers and fields. Also, the skills and techniques you learn here will help improve your critical thinking and problem-solving skills. This is a great benefit of studying mathematics and will be useful in your life in ways you may not see right now.
Solve Equations Using the Subtraction and Addition Properties of Equality
We began our work solving equations in previous chapters. It has been a while since we have seen an equation, so we will review some of the key concepts before we go any further.
We said that solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that make each side of the equation the same. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle.
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
In the earlier sections, we listed the steps to determine if a value is a solution. We restate them here.
Step 1. Substitute the number for the variable in the equation.
Step 2. Simplify the expressions on both sides of the equation.
Step 3. Determine whether the resulting equation is true.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
Determine whether y = \(\dfrac{3}{4}\) is a solution for 4y + 3 = 8y.
Solution
| Substitute \(\textcolor{red}{\dfrac{3}{4}}\) for y. | $$4 \left(\textcolor{red}{\dfrac{3}{4}}\right) + 3 \stackrel{?}{=} 8 \left(\textcolor{red}{\dfrac{3}{4}}\right)$$ |
| Multiply. | $$3 + 3 \stackrel{?}{=} 6$$ |
| Add. | $$6 = 6\; \checkmark$$ |
Since y = \(\dfrac{3}{4}\) results in a true equation, \(\dfrac{3}{4}\) is a solution to the equation 4y + 3 = 8y.
Is y = \(\dfrac{2}{3}\) a solution for 9y + 2 = 6y?
- Answer
-
no
Is y = \(\dfrac{2}{5}\) a solution for 5y − 3 = 10y?
- Answer
-
no
We introduced the Subtraction and Addition Properties of Equality in Solving Equations Using the Subtraction and Addition Properties of Equality. In that section, we modeled how these properties work and then applied them to solving equations with whole numbers. We used these properties again each time we introduced a new system of numbers. Let’s review those properties here.
Subtraction Property of Equality
For all real numbers a, b, and c, if a = b, then a − c = b − c.
Addition Property of Equality
For all real numbers a, b, and c, if a = b, then a + c = b + c.
When you add or subtract the same quantity from both sides of an equation, you still have equality.
We introduced the Subtraction Property of Equality earlier by modeling equations with envelopes and counters. Figure \(\PageIndex{1}\) models the equation x + 3 = 8.
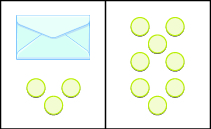
Figure \(\PageIndex{1}\)
The goal is to isolate the variable on one side of the equation. So we ‘took away’ 3 from both sides of the equation and found the solution x = 5.
Some people picture a balance scale, as in Figure \(\PageIndex{2}\), when they solve equations.
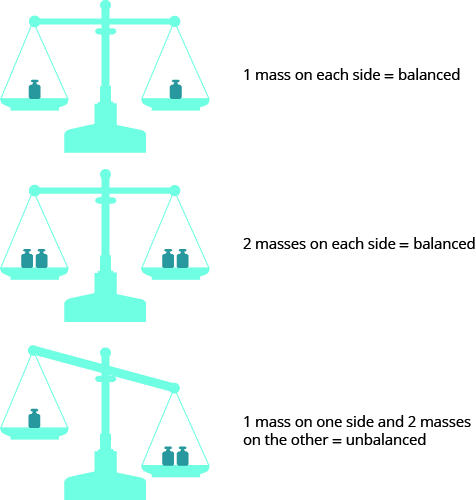
Figure \(\PageIndex{2}\)
The quantities on both sides of the equal sign in an equation are equal, or balanced. Just as with the balance scale, whatever you do to one side of the equation you must also do to the other to keep it balanced.
Let’s review how to use Subtraction and Addition Properties of Equality to solve equations. We need to isolate the variable on one side of the equation. And we check our solutions by substituting the value into the equation to make sure we have a true statement.
Solve: x + 11 = −3.
Solution
To isolate x, we undo the addition of 11 by using the Subtraction Property of Equality.
| Subtract 11 from each side to "undo" the addition. | $$x + 11 \textcolor{red}{-11} = -3 \textcolor{red}{-11}$$ |
| Simplify. | $$x = -14$$ |
Check:
| Substitute x = −14. | $$\textcolor{red}{-14} + 11 \stackrel{?}{=} -3$$ |
| $$-3 = -3\; \checkmark$$ |
Since x = −14 makes x + 11 = −3 a true statement, we know that it is a solution to the equation.
Solve: x + 9 = −7.
- Answer
-
x = -16
Solve: x + 16 = −4.
- Answer
-
x = -20
In the original equation in the previous example, 11 was added to the x, so we subtracted 11 to ‘undo’ the addition. In the next example, we will need to ‘undo’ subtraction by using the Addition Property of Equality.
Solve: m + 4 = −5.
Solution
| Add 4 to each side to "undo" the subtraction. | $$m + 4 \textcolor{red}{-4} = -5 \textcolor{red}{-4}$$ |
| Simplify. | $$m = -9$$ |
Check:
| Substitute m = −9. | $$\textcolor{red}{-9} + 4 \stackrel{?}{=} -5$$ |
| $$-5 = -5\; \checkmark$$ |
The solution to m + 4 = −5 is m = −9.
Solve: n − 6 = −7.
- Answer
-
n = -1
Solve: x − 5 = −9.
- Answer
-
x = -4
Now let’s review solving equations with fractions.
Solve: n − \(\dfrac{3}{8}\) = \(\dfrac{1}{2}\).
Solution
| Use the Addition Property of Equality. | $$n - \dfrac{3}{8} \textcolor{red}{+ \dfrac{3}{8}} = \dfrac{1}{2} \textcolor{red}{+ \dfrac{3}{8}}$$ |
| Find the LCD to add the fractions on the right. | $$n - \dfrac{3}{8} + \dfrac{3}{8} = \dfrac{4}{8} + \dfrac{3}{8}$$ |
| Simplify. | $$n = \dfrac{7}{8}$$ |
Check:
| Substitute n = \(\textcolor{red}{\dfrac{7}{8}}\). | $$\textcolor{red}{\dfrac{7}{8}} - \dfrac{3}{8} \stackrel{?}{=} \dfrac{1}{2}$$ |
| Subtract. | $$\dfrac{4}{8} \stackrel{?}{=} \dfrac{1}{2}$$ |
| Simplify. | $$\dfrac{1}{2} = \dfrac{1}{2}\; \checkmark$$ |
The solution checks.
Solve: p − \(\dfrac{1}{3}\) = \(\dfrac{5}{6}\).
- Answer
-
\(p = \frac{7}{6}\)
Solve: q − \(\dfrac{1}{2}\) = \(\dfrac{1}{6}\).
- Answer
-
\( q = \frac{2}{3}\)
In Solve Equations with Decimals, we solved equations that contained decimals. We’ll review this next.
Solve a − 3.7 = 4.3.
Solution
| Use the Addition Property of Equality. | $$a - 3.7 \textcolor{red}{+3.7} = 4.3 \textcolor{red}{+3.7}$$ |
| Add. | $$a = 8$$ |
Check:
| Substitute a = 8. | $$\textcolor{red}{8} - 3.7 \stackrel{?}{=} 4.3$$ |
| Simplify. | $$4.3 = 4.3\; \checkmark$$ |
The solution checks.
Solve: b − 2.8 = 3.6.
- Answer
-
b = 6.4
Solve: c − 6.9 = 7.1.
- Answer
-
c = 14
Solve Equations That Need to Be Simplified
In the examples up to this point, we have been able to isolate the variable with just one operation. Many of the equations we encounter in algebra will take more steps to solve. Usually, we will need to simplify one or both sides of an equation before using the Subtraction or Addition Properties of Equality. You should always simplify as much as possible before trying to isolate the variable.
Solve: 3x − 7 − 2x − 4 = 1.
Solution
The left side of the equation has an expression that we should simplify before trying to isolate the variable.
| Rearrange the terms, using the Commutative Property of Addition. | $$3x - 2x - 7 - 4 = 1$$ |
| Combine like terms. | $$x - 11 = 1$$ |
| Add 11 to both sides to isolate x. | $$x - 11 \textcolor{red}{+11} = 1 \textcolor{red}{+11}$$ |
| Simplify. | $$x = 12$$ |
| Check. Substitute x = 12 into the original equation. | $$\begin{split} 3x - 2x - 7 - 4 &= 1 \\ 3 (\textcolor{red}{12}) - 7 - 2 (\textcolor{red}{12}) - 4 &= 1 \\ 36 - 7 - 24 - 4 &= 1 \\ 29 - 24 - 4 &= 1 \\ 5 - 4 &= 1 \\ 1 &= 1\; \checkmark \end{split}$$ |
The solution checks.
Solve: 8y − 4 − 7y − 7 = 4.
- Answer
-
y = 15
Solve: 6z + 5 − 5z − 4 = 3.
- Answer
-
z = 2
Solve: 3(n − 4) − 2n = −3.
Solution
The left side of the equation has an expression that we should simplify.
| Distribute on the left. | $$3n - 12 - 2n = -3$$ |
| Use the Commutative Property to rearrange terms. | $$3n - 2n - 12 = -3$$ |
| Combine like terms. | $$n - 12 = -3$$ |
| Isolate n using the Addition Property of Equality. | $$n - 12 \textcolor{red}{+12} = -3 \textcolor{red}{+12}$$ |
| Simplify. | $$n = 9$$ |
| Check. Substitute n = 9 into the original equation. | $$\begin{split} 3(n-4) - 2n &= -3 \\ 3(\textcolor{red}{9} - 4) - 2 \cdot \textcolor{red}{9} &= -3 \\ 3(5) - 18 &= -3 \\ 15 - 18 &= -3 \\ -3 &= -3\; \checkmark \end{split}$$ |
The solution checks.
Solve: 5(p − 3) − 4p = −10.
- Answer
-
p = 5
Solve: 4(q + 2) − 3q = −8.
- Answer
-
q = -16
Solve: 2(3k − 1) − 5k = −2 − 7.
Solution
Both sides of the equation have expressions that we should simplify before we isolate the variable.
| Distribute on the left, subtract on the right. | $$6k - 2 - 5k = -9$$ |
| Use the Commutative Property of Addition. | $$6k - 5k - 2 = -9$$ |
| Combine like terms. | $$k - 2 = -9$$ |
| Undo subtraction by using the Addition Property of Equality. | $$k - 2 \textcolor{red}{+2} = -9 \textcolor{red}{+2}$$ |
| Simplify. | $$k = -7$$ |
| Check. Let k = −7. | \[\begin{split} 2(3k - 1) - 5k &= -2 - 7 \\ 2[3(\textcolor{red}{-7}) -1] - 5(\textcolor{red}{-7}) &= -2 - 7 \\ 2(-21 - 1) - 5 (-7) &= -9 \\ 2(-22) + 35 &= -9 \\ -9 &= -9\; \checkmark \end{split}$$ |
The solution checks.
Solve: 4(2h − 3) − 7h = −6 − 7.
- Answer
-
h = -1
Solve: 2(5x + 2) − 9x = −2 + 7.
- Answer
-
x = 1
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


