9.9: Solve Geometry Applications- Volume and Surface Area (Part 1)
- Page ID
- 5010
- Find volume and surface area of rectangular solids
- Find volume and surface area of spheres
- Find volume and surface area of cylinders
- Find volume of cones
Before you get started, take this readiness quiz.
- Evaluate x3 when x = 5. If you missed this problem, review Example 2.3.3.
- Evaluate 2x when x = 5. If you missed this problem, review Example 2.3.4.
- Find the area of a circle with radius \(\dfrac{7}{2}\). If you missed this problem, review Example 5.6.12.
In this section, we will finish our study of geometry applications. We find the volume and surface area of some three-dimensional figures. Since we will be solving applications, we will once again show our Problem-Solving Strategy for Geometry Applications.
- Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
- Step 2. Identify what you are looking for.
- Step 3. Name what you are looking for. Choose a variable to represent that quantity.
- Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Step 5. Solve the equation using good algebra techniques.
- Step 6. Check the answer in the problem and make sure it makes sense.
- Step 7. Answer the question with a complete sentence.
Find Volume and Surface Area of Rectangular Solids
A cheerleading coach is having the squad paint wooden crates with the school colors to stand on at the games. (See Figure \(\PageIndex{1}\)). The amount of paint needed to cover the outside of each box is the surface area, a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure.

Figure \(\PageIndex{1}\) - This wooden crate is in the shape of a rectangular solid.
Each crate is in the shape of a rectangular solid. Its dimensions are the length, width, and height. The rectangular solid shown in Figure \(\PageIndex{2}\) has length 4 units, width 2 units, and height 3 units. Can you tell how many cubic units there are altogether? Let’s look layer by layer.
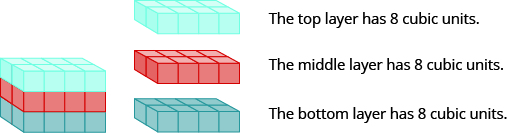
Figure \(\PageIndex{2}\) - Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. This 4 by 2 by 3 rectangular solid has 24 cubic units.
Altogether there are 24 cubic units. Notice that 24 is the length × width × height.

The volume, V, of any rectangular solid is the product of the length, width, and height.
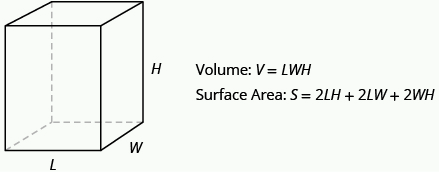
\[V= LWH\]
We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, B, is equal to length × width.
\[B = L \cdot W\]
We can substitute B for L • W in the volume formula to get another form of the volume formula.
\[\begin{split} V &= \textcolor{red}{L \cdot W} \cdot H \\ V &= \textcolor{red}{(L \cdot W)} \cdot H \\ V &= \textcolor{red}{B} h \end{split}\]
We now have another version of the volume formula for rectangular solids. Let’s see how this works with the 4 × 2 × 3 rectangular solid we started with. See Figure \(\PageIndex{3}\).
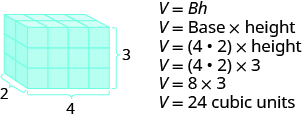
Figure \(\PageIndex{3}\)
To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them.
\[\begin{split} A_{front} &= L \times W \qquad A_{side} = L \times W \qquad A_{top} = L \times W \\ A_{front} &= 4 \cdot 3 \qquad \quad \; A_{side} = 2 \cdot 3 \qquad \quad \; A_{top} = 4 \cdot 2 \\ A_{front} &= 12 \qquad \qquad A_{side} = 6 \qquad \qquad \; \; A_{top} = 8 \end{split}\]
Notice for each of the three faces you see, there is an identical opposite face that does not show.
\[\begin{split} S &= (front + back)+(left\; side + right\; side) + (top + bottom) \\ S &= (2 \cdot front) + (2 \cdot left\; side) + (2 \cdot top) \\ S &= 2 \cdot 12 + 2 \cdot 6 + 2 \cdot 8 \\ S &= 24 + 12 + 16 \\ S &= 52\; sq.\; units \end{split}\]
The surface area S of the rectangular solid shown in Figure \(\PageIndex{3}\) is 52 square units.
In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and its width (see Figure \(\PageIndex{4}\)). Find the area of each face that you see and then multiply each area by two to account for the face on the opposite side.
\[S = 2LH + 2LW + 2WH\]
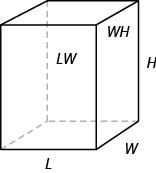
Figure \(\PageIndex{4}\) - For each face of the rectangular solid facing you, there is another face on the opposite side. There are 6 faces in all.
For a rectangular solid with length L, width W, and height H:
For a rectangular solid with length 14 cm, height 17 cm, and width 9 cm, find the (a) volume and (b) surface area.
Solution
Step 1 is the same for both (a) and (b), so we will show it just once.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 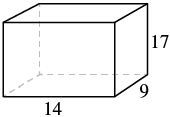 |
(a)
| Step 2. Identify what you are looking for. | the volume of the rectangular solid |
| Step 3. Name. Choose a variable to represent it. | Let V = volume |
| Step 4. Translate. Write the appropriate formula. Substitute. | $$\begin{split} V &= LWH \\ V &= 14 \cdot 9 \cdot 9 \cdot 17 \end{split}$$ |
| Step 5. Solve the equation. | $$V = 2,142$$ |
| Step 6. Check. | We leave it to you to check your calculations. |
| Step 7. Answer the question. | The volume is 2,142 cubic centimeters. |
(b)
| Step 2. Identify what you are looking for. | the surface area of the solid |
| Step 3. Name. Choose a variable to represent it. | Let S = surface area |
| Step 4. Translate. Write the appropriate formula. Substitute. | $$\begin{split} S &= 2LH + 2LW + 2WH \\ S &= 2(14 \cdot 17) + 2(14 \cdot 9) + 2(9 \cdot 17) \end{split}$$ |
| Step 5. Solve the equation. | $$S = 1,034$$ |
| Step 6. Check. | Double-check with a calculator. |
| Step 7. Answer the question. | The surface area is 1,034 square centimeters. |
Find the (a) volume and (b) surface area of rectangular solid with the: length 8 feet, width 9 feet, and height 11 feet.
- Answer a
-
792 cu. ft
- Answer b
-
518 sq. ft
Find the (a) volume and (b) surface area of rectangular solid with the: length 15 feet, width 12 feet, and height 8 feet.
- Answer a
-
1,440 cu. ft
- Answer b
-
792 sq. ft
A rectangular crate has a length of 30 inches, width of 25 inches, and height of 20 inches. Find its (a) volume and (b) surface area.
Solution
Step 1 is the same for both (a) and (b), so we will show it just once.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 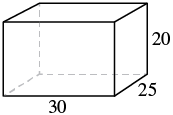 |
(a)
| Step 2. Identify what you are looking for. | the volume of the crate |
| Step 3. Name. Choose a variable to represent it. | let V = volume |
| Step 4. Translate. Write the appropriate formula. Substitute. | $$\begin{split} V &= LWH \\ V &= 30 \cdot 25 \cdot 20 \end{split}$$ |
| Step 5. Solve the equation. | $$V = 15,000$$ |
| Step 6. Check. | Double check your math. |
| Step 7. Answer the question. | The volume is 15,000 cubic inches. |
(b)
| Step 2. Identify what you are looking for. | the surface area of the crate |
| Step 3. Name. Choose a variable to represent it. | the surface area of the crate |
| Step 4. Translate. Write the appropriate formula. Substitute. | $$\begin{split} S &= 2LH + 2LW + 2WH \\ S &= 2(30 \cdot 20) + 2(30 \cdot 25) + 2(25 \cdot 20) \end{split}$$ |
| Step 5. Solve the equation. | $$S = 3,700$$ |
| Step 6. Check. | Check it yourself! |
| Step 7. Answer the question. | The surface area is 3,700 square inches. |
A rectangular box has length 9 feet, width 4 feet, and height 6 feet. Find its (a) volume and (b) surface area.
- Answer a
-
216 cu. ft
- Answer b
-
228 sq. ft
A rectangular suitcase has length 22 inches, width 14 inches, and height 9 inches. Find its (a) volume and (b) surface area.
- Answer a
-
2,772 cu. in
- Answer b
-
1,264 sq. in.
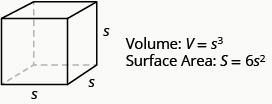
Volume and Surface Area of a Cube
A cube is a rectangular solid whose length, width, and height are equal. See Volume and Surface Area of a Cube, below. Substituting, s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get:
\[\begin{split} V &= LWH \quad \; S = 2LH + 2LW + 2WH \\ V &= s \cdot s \cdot s \quad S = 2s \cdot s + 2s \cdot s + 2s \cdot s \\ V &= s^{3} \qquad \quad S = 2s^{2} + 2s^{2} + 2s^{2} \\ &\qquad \qquad \quad \; S = 6s^{2} \end{split}\]
So for a cube, the formulas for volume and surface area are V = s3 and S = 6s2.
For any cube with sides of length s,
A cube is 2.5 inches on each side. Find its (a) volume and (b) surface area.
Solution
Step 1 is the same for both (a) and (b), so we will show it just once.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 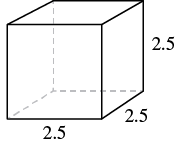 |
(a)
| Step 2. Identify what you are looking for. | the volume of the crate |
| Step 3. Name. Choose a variable to represent it. | let V = volume |
| Step 4. Translate. Write the appropriate formula. | $$V = s^{3}$$ |
| Step 5. Solve. Substitute and solve. | $$\begin{split} V &= (2.5)^{3} \\ V &= 15.625 \end{split}$$ |
| Step 6. Check. | Check your work. |
| Step 7. Answer the question. | The volume is 15.625 cubic inches. |
(b)
| Step 2. Identify what you are looking for. | the surface area of the crate |
| Step 3. Name. Choose a variable to represent it. | the surface area of the crate |
| Step 4. Translate. Write the appropriate formula. | $$S = 6s^{2}$$ |
| Step 5. Solve. Substitute and solve. | $$\begin{split} S &= 6 \cdot (2.5)^{2} \\ S &= 37.5 \end{split}$$ |
| Step 6. Check. | The check is left to you. |
| Step 7. Answer the question. | The surface area is 37.5 square inches. |
For a cube with side 4.5 meters, find the (a) volume and (b) surface area of the cube.
- Answer a
-
91.125 cu. m
- Answer b
-
121.5 sq. m
For a cube with side 7.3 yards, find the (a) volume and (b) surface area of the cube.
- Answer a
-
389.017 cu. yd.
- Answer b
-
319.74 sq. yd.
A notepad cube measures 2 inches on each side. Find its (a) volume and (b) surface area.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 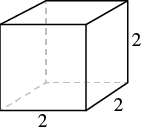 |
(a)
| Step 2. Identify what you are looking for. | the volume of the crate |
| Step 3. Name. Choose a variable to represent it. | let V = volume |
| Step 4. Translate. Write the appropriate formula. | $$V = s^{3}$$ |
| Step 5. Solve the equation. | $$\begin{split} V &= 2^{3} \\ V &= 8 \end{split}$$ |
| Step 6. Check. | Check that you did the calculations correctly. |
| Step 7. Answer the question. | The volume is 8 cubic inches |
(b)
| Step 2. Identify what you are looking for. | the surface area of the crate |
| Step 3. Name. Choose a variable to represent it. | the surface area of the crate |
| Step 4. Translate. Write the appropriate formula. | $$S = 6s^{2}$$ |
| Step 5. Solve the equation. | $$\begin{split} S &= 6 \cdot 2^{2} \\ S &= 24 \end{split}$$ |
| Step 6. Check. | The check is left to you. |
| Step 7. Answer the question. | The surface area is 24 square inches. |
A packing box is a cube measuring 4 feet on each side. Find its (a) volume and (b) surface area.
- Answer a
-
64 cu. ft
- Answer b
-
96 sq. ft
A wall is made up of cube-shaped bricks. Each cube is 16 inches on each side. Find the (a) volume and (b) surface area of each cube.
- Answer a
-
4,096 cu. in.
- Answer b
-
1,536
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


