10.9: Integer Exponents and Scientific Notation (Part 2)
- Page ID
- 7274
Convert from Decimal Notation to Scientific Notation
Remember working with place value for whole numbers and decimals? Our number system is based on powers of 10. We use tens, hundreds, thousands, and so on. Our decimal numbers are also based on powers of tens—tenths, hundredths, thousandths, and so on.
Consider the numbers 4000 and 0.004. We know that 4000 means 4 × 1000 and 0.004 means 4 × \(\dfrac{1}{1000}\). If we write the 1000 as a power of ten in exponential form, we can rewrite these numbers in this way:
\[\begin{split} &4000 \qquad \qquad 0.004 \\ &4 \times 1000 \qquad 4 \times \dfrac{1}{1000} \\ &4 \times 10^{3} \qquad \; \; 4 \times \dfrac{1}{10^{3}} \\ &\qquad \qquad \quad \; \; \; 4 \times 10^{-3} \end{split}\]
When a number is written as a product of two numbers, where the first factor is a number greater than or equal to one but less than 10, and the second factor is a power of 10 written in exponential form, it is said to be in scientific notation.
A number is expressed in scientific notation when it is of the form a × 10n where a ≥ 1 and a < 10 and n is an integer.
It is customary in scientific notation to use × as the multiplication sign, even though we avoid using this sign elsewhere in algebra.
Scientific notation is a useful way of writing very large or very small numbers. It is used often in the sciences to make calculations easier.
If we look at what happened to the decimal point, we can see a method to easily convert from decimal notation to scientific notation.

In both cases, the decimal was moved 3 places to get the first factor, 4, by itself.
- The power of 10 is positive when the number is larger than 1: 4000 = 4 × 103.
- The power of 10 is negative when the number is between 0 and 1: 0.004 = 4 × 10−3.
Write 37,000 in scientific notation.
Solution
| Step 1: Move the decimal point so that the first factor is greater than or equal to 1 but less than 10. | 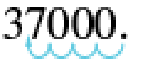 |
| Step 2: Count the number of decimal places, n, that the decimal point was moved. |
3.70000 4 places |
| Step 3: Write the number as a product with a power of 10. | 3.7×104 |
|
If the original number is:
|
|
| Step 4: Check.104 is 10,000 and 10,000 times 3.7 will be 37,000. | 37,000 = 3.7×104 |
Write in scientific notation: 96,000.
- Answer
-
9.6 × 104
Write in scientific notation: 48,300.
- Answer
-
4.83 × 104
Step 1. Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
Step 2. Count the number of decimal places, n, that the decimal point was moved.
Step 3. Write the number as a product with a power of 10.
If the original number is:
- greater than 1, the power of 10 will be 10n.
- between 0 and 1, the power of 10 will be 10−n.
Step 4. Check.
Write in scientific notation: 0.0052.
Solution
| Move the decimal point to get 5.2, a number between 1 and 10. | 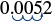 |
| Count the number of decimal places the point was moved. | 3 places |
| Write as a product with a power of 10. | 5.2 × 10−3 |
| Check your answer: | $$\begin{split} 5.2 &\times 10^{-3} \\ 5.2 &\times \dfrac{1}{10^{3}} \\ 5.2 &\times \dfrac{1}{1000} \\ 5.2 &\times 0.001 \\ 0.&0052 \end{split}$$ |
| 0.0052 = 5.2 × 10−3 |
Write in scientific notation: 0.0078.
- Answer
-
7.8 × 10-3
Write in scientific notation: 0.0129.
- Answer
-
1.29 × 10-2
Convert Scientific Notation to Decimal Form
How can we convert from scientific notation to decimal form? Let’s look at two numbers written in scientific notation and see.
\[\begin{split} &9.12 \times 10^{4} \qquad \qquad 9.12 \times 10^{-4} \\ &9.12 \times 10,000 \qquad 9.12 \times 0.0001 \\ &91,200 \qquad \qquad \quad 0.000912 \end{split}\]
If we look at the location of the decimal point, we can see an easy method to convert a number from scientific notation to decimal form.

In both cases the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.
Convert to decimal form: 6.2 × 103.
Solution
| Step 1: Determine the exponent, n, on the factor 10. | 6.2 × 103 |
| Step 2: Move the decimal point n places, adding zeros if needed. | 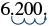 |
|
6,200 |
| Step 3: Check to see if your answer makes sense. | |
| 103 is 1000 and 1000 times 6.2 will be 6,200. | 6.2 × 103 = 6,200 |
Convert to decimal form: 1.3 × 103.
- Answer
-
1,300
Convert to decimal form: 9.25 × 104.
- Answer
-
92,500
Step 1. Determine the exponent, n, on the factor 10.
Step 2. Move the decimal n places, adding zeros if needed.
- If the exponent is positive, move the decimal point n places to the right.
- If the exponent is negative, move the decimal point |n| places to the left.
Step 3. Check.
Convert to decimal form: 8.9 × 10−2.
Solution
| Determine the exponent n, on the factor 10. | The exponent is −2. |
| Move the decimal point 2 places to the left. |  |
| Add zeros as needed for placeholders. | 0.089 |
| 8.9 × 10−2 = 0.089 | |
| The Check is left to you. |
Convert to decimal form: 1.2 × 10−4.
- Answer
-
0.00012
Convert to decimal form: 7.5 × 10−2.
- Answer
-
0.075
Multiply and Divide Using Scientific Notation
We use the Properties of Exponents to multiply and divide numbers in scientific notation.
Multiply. Write answers in decimal form: (4 × 105)(2 × 10−7).
Solution
| Use the Commutative Property to rearrange the factors. | 4 • 2 • 105 • 10−7 |
| Multiply 4 by 2 and use the Product Property to multiply 105 by 10−7. | 8 × 10−2 |
| Change to decimal form by moving the decimal two places left. | 0.08 |
Multiply. Write answers in decimal form: (3 × 106)(2 × 10−8).
- Answer
-
0.06
Multiply. Write answers in decimal form: (3 × 10−2)(3 × 10−1).
- Answer
-
0.009
Divide. Write answers in decimal form: \(\dfrac{9 \times 10^{3}}{3 \times 10^{−2}}\).
Solution
| Separate the factors. | $$\dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}$$ |
| Divide 9 by 3 and use the Quotient Property to divide 103 by 10−2. | 3 × 105 |
| Change to decimal form by moving the decimal five places right. | 300,000 |
Divide. Write answers in decimal form:\dfrac{8 \times 10^{4}}{2 \times 10^{-1}}.
- Answer
-
400,000
Divide. Write answers in decimal form:\dfrac{8 \times 10^{2}}{4 \times 10^{-2}}.
- Answer
-
20,000
Negative Exponents
Examples of Simplifying Expressions with Negative Exponents
Scientific Notation
Practice Makes Perfect
Use the Definition of a Negative Exponent
In the following exercises, simplify.
- 5−3
- 8−2
- 3−4
- 2−5
- 7−1
- 10−1
- 2−3 + 2−2
- 3−2 + 3−1
- 3−1 + 4−1
- 10−1 + 2−1
- 100 − 10−1 + 10−2
- 20 − 2−1 + 2−2
- (a) (−6)−2 (b) −6−2
- (a) (−8)−2 (b) −8−2
- (a) (−10)−4 (b) −10−4
- (a) (−4)−6 (b) −4−6
- (a) 5 • 2−1 (b) (5 • 2)−1
- (a) 10 • 3−1 (b) (10 • 3)−1
- (a) 4 • 10−3 (b) (4 • 10)−3
- (a) 3 • 5−2 (b) (3 • 5)−2
- n−4
- p−3
- c−10
- m−5
- (a) 4x−1 (b) (4x)−1 (c) (−4x)−1
- (a) 3q−1 (b) (3q)−1 (c) (−3q)−1
- (a) 6m−1 (b) (6m)−1 (c) (−6m)−1
- (a) 10k−1 (b) (10k)−1 (c) (−10k)−1
Simplify Expressions with Integer Exponents
In the following exercises, simplify.
- p−4 • p8
- r−2 • r5
- n−10 • n2
- q−8 • q3
- k−3 • k−2
- z−6 • z −2
- a • a−4
- m • m−2
- p5 • p−2 • p−4
- x4 • x−2 • x−3
- a3b−3
- u2 v−2
- (x5y−1)(x−10 y−3)
- (a3b−3)(a−5b−1)
- (uv−2)(u−5v−4)
- (pq−4)(p−6q−3)
- (−2r−3s9)(6r4s−5)
- (−3p−5q8)(7p2q−3)
- (−6m−8n−5)(−9m4n2)
- (−8a−5b−4)(−4a2b3)
- (a3)−3
- (q10)−10
- (n2)−1
- (x4)−1
- (y−5)4
- (p−3)2
- (q−5)−2
- (m−2)−3
- (4y−3)2
- (3q−5)2
- (10p−2)−5
- (2n−3)−6
- u9u−2
- b5b−3
- x−6x4
- m5m−2
- q3q12
- r6r9
- n−4n−10
- p−3p−6
Convert from Decimal Notation to Scientific Notation
In the following exercises, write each number in scientific notation.
- 45,000
- 280,000
- 8,750,000
- 1,290,000
- 0.036
- 0.041
- 0.00000924
- 0.0000103
- The population of the United States on July 4, 2010 was almost 310,000,000.
- The population of the world on July 4, 2010 was more than 6,850,000,000.
- The average width of a human hair is 0.0018 centimeters.
- The probability of winning the 2010 Megamillions lottery is about 0.0000000057.
Convert Scientific Notation to Decimal Form
In the following exercises, convert each number to decimal form.
- 4.1 × 102
- 8.3 × 102
- 5.5 × 108
- 1.6 × 1010
- 3.5 × 10−2
- 2.8 × 10−2
- 1.93 × 10−5
- 6.15 × 10−8
- In 2010, the number of Facebook users each day who changed their status to ‘engaged’ was 2 × 104.
- At the start of 2012, the US federal budget had a deficit of more than $1.5 × 1013.
- The concentration of carbon dioxide in the atmosphere is 3.9 × 10−4.
- The width of a proton is 1 × 10−5 of the width of an atom.
Multiply and Divide Using Scientific Notation
In the following exercises, multiply or divide and write your answer in decimal form.
- (2 × 105)(2 × 10−9)
- (3 × 102)(1 × 10−5)
- (1.6 × 10−2)(5.2 × 10−6)
- (2.1 × 10−4)(3.5 × 10−2)
- \(\dfrac{6 \times 10^{4}}{3 \times 10^{−2}}\)
- \(\dfrac{8 \times 10^{6}}{4 \times 10^{−1}}\)
- \(\dfrac{7 \times 10^{-2}}{1 \times 10^{−8}}\)
- \(\dfrac{5 \times 10^{-3}}{1 \times 10^{−10}}\)
Everyday Math
- Calories In May 2010 the Food and Beverage Manufacturers pledged to reduce their products by 1.5 trillion calories by the end of 2015.
- Write 1.5 trillion in decimal notation.
- Write 1.5 trillion in scientific notation.
- Length of a year The difference between the calendar year and the astronomical year is 0.000125 day.
- Write this number in scientific notation.
- How many years does it take for the difference to become 1 day?
- Calculator display Many calculators automatically show answers in scientific notation if there are more digits than can fit in the calculator’s display. To find the probability of getting a particular 5-card hand from a deck of cards, Mario divided 1 by 2,598,960 and saw the answer 3.848 × 10−7. Write the number in decimal notation.
- Calculator display Many calculators automatically show answers in scientific notation if there are more digits than can fit in the calculator’s display. To find the number of ways Barbara could make a collage with 6 of her 50 favorite photographs, she multiplied 50 • 49 • 48 • 47 • 46 • 45. Her calculator gave the answer 1.1441304 × 1010. Write the number in decimal notation.
Writing Exercises
- (a) Explain the meaning of the exponent in the expression 23. (b) Explain the meaning of the exponent in the expression 2−3.
- When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
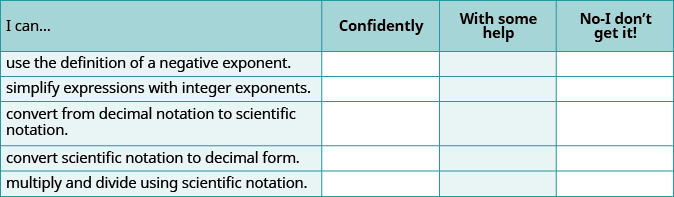
(b) After looking at the checklist, do you think you are well prepared for the next section? Why or why not?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


