10.6: Multiplication and Division of Signed Numbers

Last updated
Save as PDF

Page ID: 48897

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

be able to multiply and divide signed numbers
be able to multiply and divide signed numbers using a calculator

Multiplication of Signed Numbers

Let us consider first, the product of two positive numbers. Multiply: $3 \cdot 5$.

$3 \cdot 5$ means $5 + 5 + 5 = 15$

This suggests that (In later mathematics courses, the word "suggests" turns into the word "proof." One example does not prove a claim. Mathematical proofs are constructed to validate a claim for all possible cases.)

$\text{(positive number)} \cdot \text{(positive number)} = \text{(positive number)}$

More briefly,

(+) (+) = (+)

Now consider the product of a positive number and a negative number. Multiply: (3)(-5)

(3)(-5) means (-5) + (-5) + (-5) = -15

This suggests that

$\text{(positive number)} \cdot \text{(negative number)} = \text{(negative number)}$

More briefly,

(+) (-) = (-)

By the commutative property of multiplication, we get

$\text{(negative number)} \cdot \text{(positive number)} = \text{(negative number)}$

More briefly,

(-) (+) = (-)

The sign of the product of two negative numbers can be suggested after observing the following illustration.

Multiply -2 by, respectively, 4, 3, 2, 1, 0, -1, -2, -3, -4.

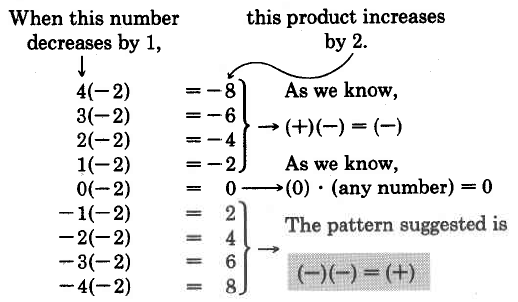
$A list of equations. 4 times negative 2 equals negative 8. 3 times negative 2 equals negative 6. 2 times negative 2 equals negative 4. 1 times negative 2 equals negative 2. For all this, the following label is listed on the side: As we know, a negative times a positive equals a negative. The list continues. 0 times negative 2 equals 0. The following label is listed to the side: As we know, 0 times any number equals 0. The list continues further. Negative 1 times negative 2 equals 2. Negative 2 times negative 2 equals 4. Negative 3 times negative 2 equals 6. Negative 4 times negative 2 equals 8. The following label is listed to the side: The pattern suggested is a negative times a negative equals a positive. For the entire list, the label at the top says: when this number decreases by 1, the first factor in each multiplication problem, the product increases by 2.$

We have the following rules for multiplying signed numbers.

Rules for Multiplying Signed Numbers
Multiplying signed numbers:

To multiply two real numbers that have the same sign, multiply their absolute values. The product is positive.
(+) (+) = (+)
(-) (-) = (+)
To multiply two real numbers that have opposite signs, multiply their absolute values. The product is negative.
(+) (-) = (-)
(-) (+) = (-)

Sample Set A

Find the following products.

$8 \cdot 6$

Solution

$\begin{array} {ccl} {|8|} & = & {8} \\ {|6|} & = & {6} \end{array} \big \}$ Multiply these absolute values.

$8 \cdot 6 = 48$

Since the numbers have the same sign, the product is positive.

Thus, $8 \cdot 6 = +48$, or $8 \cdot 6 = 48$.

Sample Set A

(-8)(-6)

Solution

$\begin{array} {ccl} {|-8|} & = & {8} \\ {|-6|} & = & {6} \end{array} \big \}$ Multiply these absolute values.

$8 \cdot 6 = 48$

Since the numbers have the same sign, the product is positive.

Thus, $(-8)(-6) = +48$, or $(-8)(-6) = 48$.

Sample Set A

(-4)(7)

Solution

$\begin{array} {ccl} {|-4|} & = & {4} \\ {|7|} & = & {7} \end{array} \big \}$ Multiply these absolute values.

$4 \cdot 7 = 28$

Since the numbers have opposite signs, the product is negative.

Thus, (-4)(7) = -28.

Sample Set A

6(-3)

Solution

$\begin{array} {ccl} {|6|} & = & {6} \\ {|-3|} & = & {3} \end{array} \big \}$ Multiply these absolute values.

$6 \cdot 3 = 18$

Since the numbers have opposite signs, the product is negative.

Thus, 6(-3) = -18.

Practice Set A

Find the following products.

3(-8)

Answer: -24

Practice Set A

4(16)

Answer: 64

Practice Set A

(-6)(-5)

Answer: 30

Practice Set A

(-7)(-2)

Answer: 14

Practice Set A

(-1)(4)

Answer: -4

Practice Set A

(-7)7

Answer: -49

Division of Signed Numbers

To determine the signs in a division problem, recall that

$\dfrac{12}{3} = 4$ since $12 = 3 \cdot 4$

This suggests that

$\dfrac{(+)}{(+)} = (+)$

$\dfrac{(+)}{(+)} = (+)$ since (+) = (+) (+)

What is $\dfrac{12}{-3}$?

12 = (-3)(-4) suggets that $\dfrac{12}{-3} = -4$. That is,

$\dfrac{(+)}{(-)} = (-)$

(+) = (-) (-) suggets that $\dfrac{(+)}{(-)} = (-)$

What is $\dfrac{-12}{3}$?

-12 = (3)(-4) suggests that $\dfrac{-12}{3} = -4$. That is,

$\dfrac{(-)}{(+)} = (-)$

(-) = (+) (-) suggets that $\dfrac{(-)}{(+)} = (-)$

What is $\dfrac{-12}{-3}$?

-12 = (-3)(4) suggets that $\dfrac{-12}{-3} = 4$. That is,

$\dfrac{(-)}{(-)} = (+)$

(-) = (-)(+) suggests that $\dfrac{(-)}{(-)} = (+)$

We have the following rules for dividing signed numbers.

Rules for Dividing Signed Numbers
Dividing signed numbers:

To divide two real numbers that have the same sign, divide their absolute values. The quotient is positive.
$\dfrac{(+)}{(+)} = (+)\dfrac{(-)}{(-)} = (+)$
To divide two real numbers that have opposite signs, divide their absolute values. The quotient is negative.
$\dfrac{(-)}{(+)} = (-)\dfrac{(+)}{(-)} = (-)$

Sample Set B

Find the following quotients.

$\dfrac{-10}{2}$

Solution

$\begin{array} {ccc} {|-10|} & = & {10} \\ {|2|} & = & {2} \end{array} \big \}$ Divide these absolute values.

$\dfrac{10}{2} = 5$

Since the numbers have opposite signs, the quotient is negative.

Thus $\dfrac{-10}{2} = -5$.

Sample Set B

$\dfrac{-35}{-7}$

Solution

$\begin{array} {ccc} {|-35|} & = & {35} \\ {|-7|} & = & {7} \end{array} \big \}$ Divide these absolute values.

$\dfrac{35}{7} = 5$

Since the numbers have the same signs, the quotient is positive.

Thus $\dfrac{-35}{-7} = 5$.

Sample Set B

$\dfrac{18}{-9}$

Solution

$\begin{array} {ccc} {|18|} & = & {18} \\ {|-9|} & = & {9} \end{array} \big \}$ Divide these absolute values.

$\dfrac{18}{9} = 2$

Since the numbers have opposite signs, the quotient is negative.

Thus $\dfrac{18}{-9} = -2$.

Practice Set B

Find the following quotients.

$\dfrac{-24}{-6}$

Answer: 4

Practice Set B

$\dfrac{30}{-5}$

Answer: -6

Practice Set B

$\dfrac{-54}{27}$

Answer: -2

Practice Set B

$\dfrac{51}{17}$

Answer: 3

Sample Set C

Find the value of $\dfrac{-6(4 - 7) - 2(8 - 9)}{-(4 + 1) + 1}$.

Solution

Using the order of operations and what we know about signed numbers, we get,

$\begin{array} {rcl} {\dfrac{-6(4 - 7) - 2(8 - 9)}{-(4 + 1) + 1}} & = & {\dfrac{-6(-3) - 2(-1)}{-(5) + 1}} \\ {} & = & {\dfrac{18 + 2}{-5 + 1}} \\ {} & = & {\dfrac{20}{-4}} \\ {} & = & {-5} \end{array}$

Practice Set C

Find the value of $\dfrac{-5(2 - 6) - 4(-8 - 1)}{2(3 - 10) - 9(-2)}$.

Answer: 14

Calculators

Calculators with the

$A box with a plus and minus sign.$

key can be used for multiplying and dividing signed numbers.

Sample Set D

Use a calculator to find each quotient or product.

$(-186) \cdot (-43)$

Solution

Since this product involves a $\text{(negative)} \cdot \text{(negative)}$, we know the result should be a positive number. We'll illustrate this on the calculator.

		Display Reads
Type	186	186
Press	$A box with a plus and minus sign.$	-186
Press	$\times$	-186
Type	43	43
Press	$A box with a plus and minus sign.$	-43
Press	=	7998

Thus, $(-186) \cdot (-43) = 7,998$

Sample Set D

$\dfrac{158.64}{-54.3}$. Round to one decimal place.

Solution

Since this product involves a $\text{(negative)} \cdot \text{(negative)}$, we know the result should be a positive number. We'll illustrate this on the calculator.

		Display Reads
Type	158.64	158.64
Press	$\div$	158.64
Type	54.3	54.3
Press	$A box with a plus and minus sign.$	-54.3
Press	=	-2.921546961

Rounding to one decimal place we get -2.9.

Practice Set D

Use a calculator to find each value.

$(-51.3) \cdot (-21.6)$

Answer: 1,108.08

Practice Set D

$-2.5746 \div -2.1$

Answer: 1.226

Practice Set D

$(0.006) \cdot (-0.241)$. Round to three decimal places.

Answer: -0.001

Exercises

Find the value of each of the following. Use a calculator to check each result.

Exercise $\PageIndex{1}$

(-2)(-8)

Answer: 16

Exercise $\PageIndex{2}$

(-3)(-9)

Exercise $\PageIndex{3}$

(-4)(-8)

Answer: 32

Exercise $\PageIndex{4}$

(-5)(-2)

Exercise $\PageIndex{5}$

(3)(-12)

Answer: -36

Exercise $\PageIndex{6}$

(4)(-18)

Exercise $\PageIndex{7}$

(10)(-6)

Answer: -60

Exercise $\PageIndex{8}$

(-6)(4)

Exercise $\PageIndex{9}$

(-2)(6)

Answer: -12

Exercise $\PageIndex{10}$

(-8)(7)

Exercise $\PageIndex{11}$

$\dfrac{21}{7}$

Answer: 3

Exercise $\PageIndex{12}$

$\dfrac{42}{6}$

Exercise $\PageIndex{13}$

$\dfrac{-39}{3}$

Answer: -13

Exercise $\PageIndex{14}$

$\dfrac{-20}{10}$

Exercise $\PageIndex{15}$

$\dfrac{-45}{-5}$

Answer: 9

Exercise $\PageIndex{16}$

$\dfrac{-16}{-8}$

Exercise $\PageIndex{17}$

$\dfrac{25}{-5}$

Answer: -5

Exercise $\PageIndex{18}$

$\dfrac{36}{-4}$

Exercise $\PageIndex{19}$

8 - (-3)

Answer: 11

Exercise $\PageIndex{20}$

14 - (-20)

Exercise $\PageIndex{21}$

20 - (-8)

Answer: 28

Exercise $\PageIndex{22}$

(-4) - (-1)

Exercise $\PageIndex{23}$

0 - 4

Answer: -4

Exercise $\PageIndex{24}$

0 - (-1)

Exercise $\PageIndex{25}$

-6 + 1 - 7

Answer: -12

Exercise $\PageIndex{26}$

15 - 12 - 20

Exercise $\PageIndex{27}$

1 - 6 - 7 + 8

Answer: -4

Exercise $\PageIndex{28}$

2 + 7 - 10 + 2

Exercise $\PageIndex{29}$

3(4 - 6)

Answer: -6

Exercise $\PageIndex{30}$

8(5 - 12)

Exercise $\PageIndex{31}$

-3(1 - 6)

Answer: 15

Exercise $\PageIndex{32}$

-8(4 - 12) + 2

Exercise $\PageIndex{33}$

-4(1 - 8) + 3(10 - 3)

Answer: 49

Exercise $\PageIndex{34}$

-9(0 - 2) + 4(8 - 9) + 0(-3)

Exercise $\PageIndex{35}$

6(-2 - 9) - 6(2 + 9) + 4(-1 - 1)

Answer: -140

Exercise $\PageIndex{36}$

$\dfrac{3(4 + 1) - 2 (5)}{-2}$

Exercise $\PageIndex{37}$

$\dfrac{4(8 + 1) - 3 (-2)}{-4 - 2}$

Answer: -7

Exercise $\PageIndex{38}$

$\dfrac{-1(3 + 2) + 5}{-1}$

Exercise $\PageIndex{39}$

$\dfrac{-3(4 - 2) + (-3)(-6)}{-4}$

Answer: -3

Exercise $\PageIndex{40}$

-1(4 + 2)

Exercise $\PageIndex{41}$

-1(6 - 1)

Answer: -5

Exercise $\PageIndex{42}$

-(8 + 21)

Exercise $\PageIndex{43}$

-(8 - 21)

Answer: 13

Exercises for Review

Exercise $\PageIndex{44}$

Use the order of operations to simplify $(5^2 + 3^2 + 2) \div 2^2$.

Exercise $\PageIndex{45}$

Find $\dfrac{3}{8}$ of $\dfrac{32}{9}$.

Answer: $\dfrac{4}{3} = 1 \dfrac{1}{3}$

Exercise $\PageIndex{46}$

Write this number in decimal form using digits: “fifty-two three-thousandths”

Exercise $\PageIndex{47}$

The ratio of chlorine to water in a solution is 2 to 7. How many mL of water are in a solution that contains 15 mL of chlorine?

Answer: $52 \dfrac{1}{2}$

Exercise $\PageIndex{48}$

Perform the subtraction -8 - (-20)