10.2: Use Multiplication Properties of Exponents (Part 1)
- Page ID
- 5013
- Simplify expressions with exponents
- Simplify expressions using the Product Property of Exponents
- Simplify expressions using the Power Property of Exponents
- Simplify expressions using the Product to a Power Property
- Simplify expressions by applying several properties
- Multiply monomials
Before you get started, take this readiness quiz.
- Simplify: \(\dfrac{3}{4} \cdot \dfrac{3}{4}\). If you missed the problem, review Example 4.3.7.
- Simplify: (−2)(−2)(−2). If you missed the problem, review Example 3.7.6.
Simplify Expressions with Exponents
Remember that an exponent indicates repeated multiplication of the same quantity. For example, 24 means to multiply four factors of 2, so 24 means 2 • 2 • 2 • 2. This format is known as exponential notation.
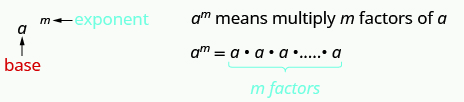
This is read a to the mth power.
In the expression am, the exponent tells us how many times we use the base a as a factor.

Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
Simplify: (a) 53 (b) 91
Solution
(a) 53
| Multiply 3 factors of 5. | 5 • 5 • 5 |
| Simplify. | 125 |
(b) 91
| Multiply 1 factor of 9. | 9 |
Simplify: (a) 43 (b) 111
- Answer a
-
64
- Answer b
-
11
Simplify: (a) 34 (b) 211
- Answer a
-
81
- Answer b
-
21
Simplify: (a) \(\left(\dfrac{7}{8}\right)^{2}\) (b) (0.74)2
Solution
(a) \(\left(\dfrac{7}{8}\right)^{2}\)
| Multiply two factors. | $$\left(\dfrac{7}{8}\right) \left(\dfrac{7}{8}\right)$$ |
| Simplify. | $$\dfrac{49}{64}$$ |
(b) (0.74)2
| Multiply two factors. | (0.74)(0.74) |
| Simplify. | 0.5476 |
Simplify: (a) \(\left(\dfrac{5}{8}\right)^{2}\) (b) (0.67)2
- Answer a
-
\(\frac{25}{64}\)
- Answer b
-
0.4489
Simplify: (a) \(\left(\dfrac{2}{5}\right)^{3}\) (b) (0.127)2
- Answer a
-
\(\frac{8}{125}\)
- Answer b
-
0.016129
Simplify: (a) (−3)4 (b) −34
Solution
(a) (−3)4
| Multiply four factors of −3. | (−3)(−3)(−3)(−3) |
| Simplify. | 81 |
(b) −34
| Multiply two factors. | −(3 • 3 • 3 • 3) |
| Simplify. | −81 |
Notice the similarities and differences in parts (a) and (b). Why are the answers different? In part (a) the parentheses tell us to raise the (−3) to the 4th power. In part (b) we raise only the 3 to the 4th power and then find the opposite.
Simplify: (a) (−2)4 (b) −24
- Answer a
-
16
- Answer b
-
-16
Simplify: (a) (−8)2 (b) −82
- Answer a
-
64
- Answer b
-
-64
Simplify Expressions Using the Product Property of Exponents
You have seen that when you combine like terms by adding and subtracting, you need to have the same base with the same exponent. But when you multiply and divide, the exponents may be different, and sometimes the bases may be different, too. We’ll derive the properties of exponents by looking for patterns in several examples. All the exponent properties hold true for any real numbers, but right now we will only use whole number exponents.
First, we will look at an example that leads to the Product Property.
| $$x^{2} \cdot x^{2}$$ | |
| What does this mean? How many factors altogether? | 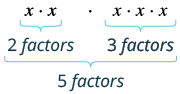 |
| So, we have | $$x^{5}$$ |
| Notice that 5 is the sum of the exponents, 2 and 3. | $$x^{2} \cdot x^{3}\; is\; x^{2+3},\; or\; x^{5}$$ |
| We write: | $$\begin{split} &x^{2} \cdot x^{3} \\ &x^{2+3} \\ &x^{5} \end{split}$$ |
The base stayed the same and we added the exponents. This leads to the Product Property for Exponents.
If a is a real number and m, n are counting numbers, then
\[a^{m} \cdot a^{n} = a^{m + n}\]
To multiply with like bases, add the exponents.
An example with numbers helps to verify this property.
\[\begin{split} 2^{2} \cdot 2^{3} &\stackrel{?}{=} 2^{2+3} \\ 4 \cdot 8 &\stackrel{?}{=} 2^{5} \\ 32 &= 32\; \checkmark \end{split}\]
Simplify: x5 • x7.
Solution
| Use the product property, am • an = am + n. | $$x^{\textcolor{red}{5+7}}$$ |
| Simplify. | $$x^{12}$$ |
Simplify: x7 • x8.
- Answer
-
x15
Simplify: x5 • x11.
- Answer
-
x16
Simplify: b4 • b.
Solution
| Rewrite, b = b1. | $$b^{4} \cdot b^{1}$$ |
| Use the product property, am • an = am + n. | $$b^{\textcolor{red}{4+1}}$$ |
| Simplify. | $$b^{5}$$ |
Simplify: p9 • p.
- Answer
-
p10
Simplify: m • m7.
- Answer
-
m8
Simplify: 27 • 29.
Solution
| Use the product property, am • an = am + n. | $$2^{\textcolor{red}{7+9}}$$ |
| Simplify. | $$2^{16}$$ |
Simplify: 6 • 69.
- Answer
-
610
Simplify: 96 • 99.
- Answer
-
915
Simplify: y17 • y23.
Solution
| Notice, the bases are the same, so add the exponents. | $$y^{\textcolor{red}{17+23}}$$ |
| Simplify. | $$y^{40}$$ |
Simplify: y24 • y19.
- Answer
-
y43
Simplify: z15 • z24.
- Answer
-
z39
We can extend the Product Property of Exponents to more than two factors.
Simplify: x3 • x4 • x2.
Solution
| Add the exponents, since the bases are the same. | $$x^{\textcolor{red}{3+4+2}}$$ |
| Simplify. | $$x^{9}$$ |
Simplify: x7 • x5 • x9.
- Answer
-
x21
Simplify: y3 • y8 • y4.
- Answer
-
y15
Simplify Expressions Using the Power Property of Exponents
Now let’s look at an exponential expression that contains a power raised to a power. See if you can discover a general property.
| $$(x^{2})^{3}$$ | |
| What does this mean? | $$x^{2} \cdot x^{2} \cdot x^{2}$$ |
| How many factors altogether? | 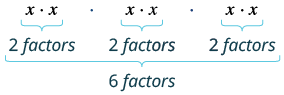 |
| So, we have | $$x^{6}$$ |
| Notice that 6 is the product of the exponents, 2 and 3. | $$(x^{2})^{3}\; is\; x^{2 \cdot 3}\; or\; x^{6}$$ |
| We write: | $$\begin{split} &(x^{2})^{3} \\ &x^{2 \cdot 3} \\ &x^{6} \end{split}$$ |
We multiplied the exponents. This leads to the Power Property for Exponents.
If a is a real number and m, n are whole numbers, then
\[(a^{m})^{n} = a^{m \cdot n}\]
To raise a power to a power, multiply the exponents.
An example with numbers helps to verify this property.
\[\begin{split} (5^{2})^{3} &\stackrel{?}{=} 5^{2 \cdot 3} \\ (25)^{3} &\stackrel{?}{=} 5^{6} \\ 15,625 &= 15,625\; \checkmark \end{split}\]
Simplify: (a) (x5)7 (b) (36)8
Solution
(a) (x5)7
| Use the Power Property, (am)n = am • n. | $$x^{\textcolor{red}{5 \cdot 7}}$$ |
| Simplify. | $$x^{35}$$ |
(b) (36)8
| Use the Power Property, (am)n = am • n. | $$3^{\textcolor{red}{6 \cdot 8}}$$ |
| Simplify. | $$x^{48}$$ |
Simplify: (a) (x7)4 (b) (74)8
- Answer a
-
x28
- Answer b
-
732
Simplify: (a) (x6)9 (b) (86)7
- Answer a
-
y54
- Answer b
-
842
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


