2.1.3: More about Constant of Proportionality

Lesson

Let's solve more problems involving proportional relationships using tables.

Exercise \(\PageIndex{1}\): Equal Measures

Use the numbers and units from the list to find as many equivalent measurements as you can. For example, you might write “30 minutes is \(\frac{1}{2}\) hour.”

You can use the numbers and units more than once.

\(\begin{array}{llll}{1}&{\frac{1}{2}}&{0.3}&{\text{centimeter}}\\{12}&{40}&{24}&{\text{meter}}\\{0.4}&{0.01}&{\frac{1}{10}}&{\text{hour}}\\{60}&{3\frac{1}{3}}&{6}&{\text{feet}}\\{50}&{30}&{2}&{\text{minute}}\\{}&{}&{\frac{2}{5}}&{\text{inch}}\end{array}\)

Exercise \(\PageIndex{2}\): Centimeters and Millimeters

There is a proportional relationship between any length measured in centimeters and the same length measured in millimeters.

Figure \(\PageIndex{1}\)

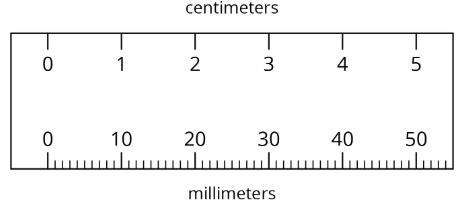
There are two ways of thinking about this proportional relationship.

1. If you know the length of something in centimeters, you can calculate its length in millimeters.
   1. Complete the table.
   2. What is the constant of proportionality?

      Table \(\PageIndex{1}\)

      length (cm)	length (mm)
      9
      12.5
      50
      88.49

2. If you know the length of something in millimeters, you can calculate its length in centimeters.
   1. Complete the table.
   2. What is the constant of proportionality?

      Table \(\PageIndex{2}\)

      length (mm)	length (cm)
      70
      245
      4
      699.1

3. How are these two constants of proportionality related to each other?
4. Complete each sentence:
   1. To convert from centimeters to millimeters, you can multiply by ________.
   2. To convert from millimeters to centimeters, you can divide by ________ or multiply by ________.

Are you ready for more?

1. How many square millimeters are there in a square centimeter?
2. How do you convert square centimeters to square millimeters? How do you convert the other way?

Exercise \(\PageIndex{3}\): Pittsburgh to Phoenix

On its way from New York to San Diego, a plane flew over Pittsburgh, Saint Louis, Albuquerque, and Phoenix traveling at a constant speed.

Complete the table as you answer the questions. Be prepared to explain your reasoning.

Figure \(\PageIndex{2}\): A United States map with 5 segments representing the distance a plane flew. The segments are New York to Pittsburgh, Pittsburgh to Saint Louis, Saint Louis to Albuquerque, Albuquerque to Phoenix and Phoenix to San Diego. By United States Census Bureau. Public Domain. American Fact Finder. Source.

Table \(\PageIndex{3}\)

segment	time	distance	speed
Pittsburgh to Saint Louis	1 hour	550 miles
Saint Louis to Albuquerque	1 hour 42 minutes
Albuquerque to Phoenix		330 miles

1. What is the distance between Saint Louis and Albuquerque?
2. How many minutes did it take to fly between Albuquerque and Phoenix?
3. What is the proportional relationship represented by this table?
4. Diego says the constant of proportionality is 550. Andre says the constant of proportionality is \(9\frac{1}{6}\). Do you agree with either of them? Explain your reasoning.

Summary

When something is traveling at a constant speed, there is a proportional relationship between the time it takes and the distance traveled. The table shows the distance traveled and elapsed time for a bug crawling on a sidewalk.

Figure \(\PageIndex{3}\): Table with 2 columns and 4 rows of data. The columns are: distance traveled (cm) and elapsed time (sec). The table has the ordered pairs (the fraction 3 over 2 comma 1), (1 comma the fraction 2 over 3), (3 comma 2) and (10 comma the fraction 20 over 3). Each pair has an arrow pointing from the value in the first column to the value in the second column. Times the fraction 2 over 3 is below the table.

We can multiply any number in the first column by \(\frac{2}{3}\) to get the corresponding number in the second column. We can say that the elapsed time is proportional to the distance traveled, and the constant of proportionality is \(\frac{2}{3}\). This means that the bug’s pace is \(\frac{2}{3}\) seconds per centimeter.

This table represents the same situation, except the columns are switched.

Figure \(\PageIndex{4}\): Table with 2 columns and 4 rows of data. The columns are: elapsed time (sec) and distance traveled (cm). The table has the ordered pairs (1 comma the fraction 3 over 2), (the fraction 2 over 3 comma 1), (2 comma 3) and (the fraction 20 over 3 comma 10). Each pair has an arrow pointing from the value in the first column to the value in the second column. Times the fraction three over 2 is below the table.

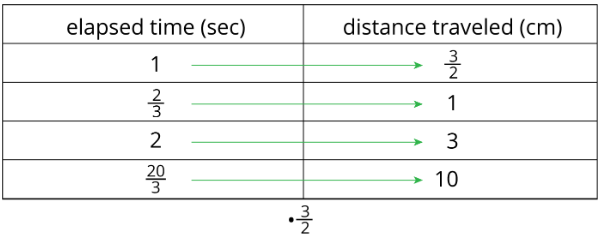
We can multiply any number in the first column by \(\frac{3}{2}\) to get the corresponding number in the second column. We can say that the distance traveled is proportional to the elapsed time, and the constant of proportionality is \(\frac{3}{2}\). This means that the bug’s speed is \(\frac{3}{2}\) centimeters per second.

Notice that \(\frac{3}{2}\) is the reciprocal of \(\frac{2}{3}\). When two quantities are in a proportional relationship, there are two constants of proportionality, and they are always reciprocals of each other. When we represent a proportional relationship with a table, we say the quantity in the second column is proportional to the quantity in the first column, and the corresponding constant of proportionality is the number we multiply values in the first column to get the values in the second.

Glossary Entries

Definition: Constant of Proportionality

In a proportional relationship, the values for one quantity are each multiplied by the same number to get the values for the other quantity. This number is called the constant of proportionality.

In this example, the constant of proportionality is 3, because \(2\cdot 3=6\), \(3\cdot 3=9\), and \(5\cdot 3=15\). This means that there are 3 apples for every 1 orange in the fruit salad.

Table \(\PageIndex{4}\)

number of oranges	number of apples
2	6
3	9
5	15

Definition: Equivalent Ratios

Two ratios are equivalent if you can multiply each of the numbers in the first ratio by the same factor to get the numbers in the second ratio. For example, \(8:6\) is equivalent to \(4:3\), because \(8\cdot\frac{1}{2}=4\) and \(6\cdot\frac{1}{2}=3\).

A recipe for lemonade says to use 8 cups of water and 6 lemons. If we use 4 cups of water and 3 lemons, it will make half as much lemonade. Both recipes taste the same, because and are equivalent ratios.

Table \(\PageIndex{5}\)

cups of water	number of lemons
8	6
4	3

Definition: Proportional Relationship

In a proportional relationship, the values for one quantity are each multiplied by the same number to get the values for the other quantity.

For example, in this table every value of \(p\) is equal to 4 times the value of \(s\) on the same row.

We can write this relationship as \(p=4s\). This equation shows that \(s\) is proportional to \(p\).

Table \(\PageIndex{6}\)

\(s\)	\(p\)
2	8
3	12
5	20
10	40

Practice

Exercise \(\PageIndex{4}\)

Noah is running a portion of a marathon at a constant speed of 6 miles per hour.

Complete the table to predict how long it would take him to run different distances at that speed, and how far he would run in different time intervals.

Table \(\PageIndex{7}\)

time in hours	miles traveled at 6 miles per hour
\(1\)
\(\frac{1}{2}\)
\(1\frac{1}{3}\)
	\(1\frac{1}{2}\)
	\(9\)
	\(4\frac{1}{2}\)

Exercise \(\PageIndex{5}\)

One kilometer is 1000 meters.

1. Complete the tables. What is the interpretation of the constant of proportionality in each case?

Table \(\PageIndex{8}\)

meters	kilometers
1,000	1
250
12
1

The constant of proportionality tells us that:

Table \(\PageIndex{9}\)

kilometers	meters
1	1,000
5
20
0.3

The constant of proportionality tells us that:

2. What is the relationship between two constants of proportionality?

Exercise \(\PageIndex{6}\)

Jada and Lin are comparing inches and feet. Jada says that the constant of proportionality is 12. Lin says it is \(\frac{1}{12}\). Do you agree with either of them? Explain your reasoning.

Exercise \(\PageIndex{7}\)

The area of the Mojave desert is 25,000 square miles. A scale drawing of the Mojave desert has an area of 10 square inches. What is the scale of the map?

(From Unit 1.2.6)

Exercise \(\PageIndex{8}\)

Which of these scales is equivalent to the scale 1 cm to 5 km? Select all that apply.

1. 3 cm to 15 km
2. 1 mm to 150 km
3. 5 cm to 1 km
4. 5 mm to 2.5 km
5. 1 mm to 500 m

(From Unit 1.2.5)

Exercise \(\PageIndex{9}\)

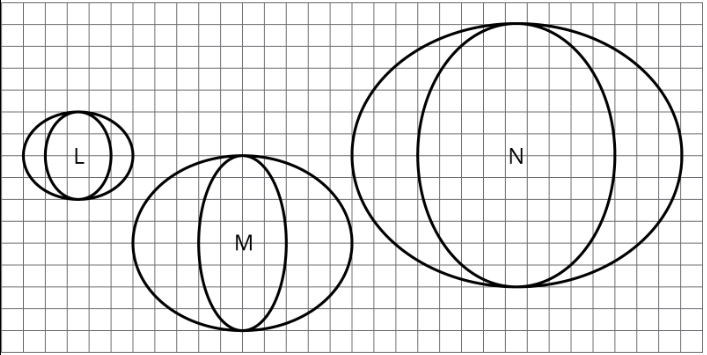
Which one of these pictures is not like the others? Explain what makes it different using ratios.

Figure \(\PageIndex{5}\)

(From Unit 2.1.1)