5.2: Angles
- Page ID
- 13859
Because many applications involving circles also involve a rotation of the circle, it is natural to introduce a measure for the rotation, or angle, between two rays (line segments) emanating from the center of a circle. The angle measurement you are most likely familiar with is degrees, so we’ll begin there.
Definition: measure of an angle
The measure 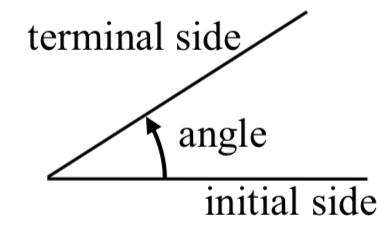 of an angle is a measurement between two intersecting lines, line segments or rays, starting at the initial side and ending at the terminal side. It is a rotational measure, not a linear measure.
of an angle is a measurement between two intersecting lines, line segments or rays, starting at the initial side and ending at the terminal side. It is a rotational measure, not a linear measure.
Measuring Angles
Definition: degrees
A degree is a measurement of angle. One full rotation around the circle is equal to 360 degrees, so one degree is 1/360 of a circle.
An angle measured in degrees should always include the unit “degrees” after the number, or include the degree symbol \(^{\circ}\). For example, 90 degrees = \(90^{\circ}\).
Definition: standard position
When measuring angles on a circle, unless otherwise directed, we measure angles in standard position: starting at the positive horizontal axis and with counter-clockwise rotation.
Example \(\PageIndex{1}\)
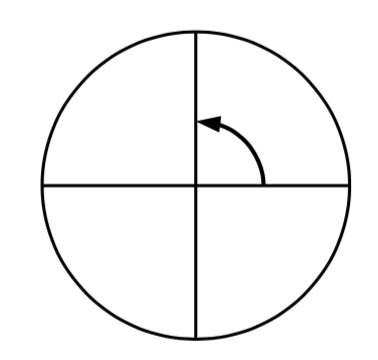
Give the degree measure of the angle shown on the circle.
Solution
The vertical and horizontal lines divide the circle into quarters. Since one full rotation is 360 degrees=\(360{}^\circ\), each quarter rotation is 360/4 = \(90^{\circ}\) or 90 degrees.
Example \(\PageIndex{2}\)
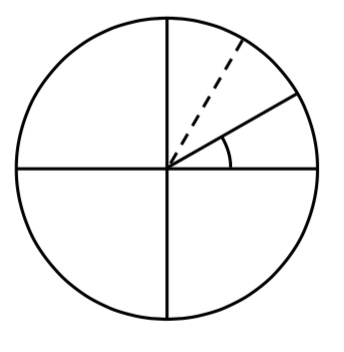
Show an angle of \(30^{\circ}\) on the circle.
Solution
An angle of \(30^{\circ}\) is 1/3 of \(90^{\circ}\), so by dividing a quarter rotation into thirds, we can sketch a line at \(30^{\circ}\).
Going Greek
When representing angles using variables, it is traditional to use Greek letters. Here is a list of commonly encountered Greek letters.
| \(\theta\) | \(varphi\) or \(\phi\) | \(\alpha\) | \(\beta\) | \(\gamma\) |
| theta | phi | alpha | beta | gamma |
Working with Angles in Degrees
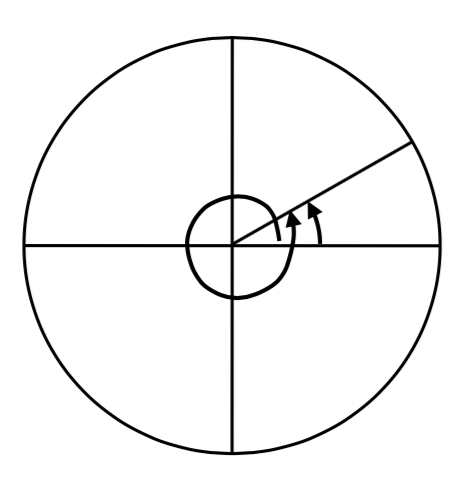 Notice that since there are 360 degrees in one rotation, an angle greater than 360 degrees would indicate more than 1 full rotation. Shown on a circle, the resulting direction in which this angle’s terminal side points would be the same as for another angle between 0 and 360 degrees. These angles would be called coterminal.
Notice that since there are 360 degrees in one rotation, an angle greater than 360 degrees would indicate more than 1 full rotation. Shown on a circle, the resulting direction in which this angle’s terminal side points would be the same as for another angle between 0 and 360 degrees. These angles would be called coterminal.
coterminal angles
After completing their full rotation based on the given angle, two angles are coterminal if they terminate in the same position, so their terminal sides coincide (point in the same direction).
Example \(\PageIndex{3}\)
Find an angle \(\theta\) that is coterminal with \(800^{\circ}\), where \(0^{\circ} \le \theta <360^{\circ}\)
Solution
Since adding or subtracting a full rotation, 360 degrees, would result in an angle with terminal side pointing in the same direction, we can find coterminal angles by adding or subtracting 360 degrees. An angle of 800 degrees is coterminal with an angle of 800 - 360 = 440 degrees. It would also be coterminal with an angle of 440 - 360 = 80 degrees.
The angle \(\theta =80^{\circ}\)is coterminal with \(800^{\circ}\).
By finding the coterminal angle between 0 and 360 degrees, it can be easier to see which direction the terminal side of an angle points in.
Exercise \(\PageIndex{1}\)
Find an angle \(\alpha\) that is coterminal with \(870^{\circ}\), where \(0^{\circ} \le \alpha <360^{\circ}\).
- Answer
-
\[\alpha =870-360-360=150^{\circ}\nonumber\]
On a number line a positive number is measured to the right and a negative number is measured in the opposite direction (to the left). Similarly a positive angle is measured counterclockwise and a negative angle is measured in the opposite direction (clockwise).
Example \(\PageIndex{4}\)
Show the angle \(-45^{\circ}\)on the circle and find a positive angle \(\alpha\) that is coterminal and \(0^{\circ} \le \alpha <360^{\circ}\).
Solution
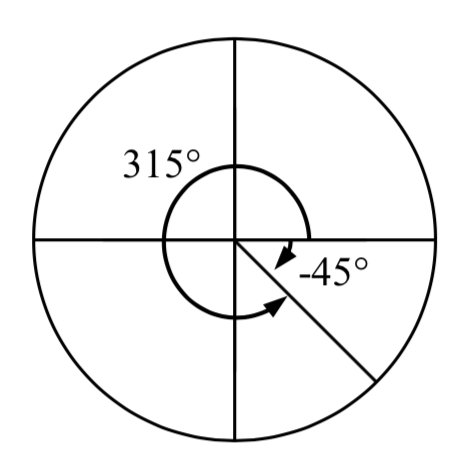
Since 45 degrees is half of 90 degrees, we can start at the positive horizontal axis and measure clockwise half of a 90 degree angle.
Since we can find coterminal angles by adding or subtracting a full rotation of 360 degrees, we can find a positive coterminal angle here by adding 360 degrees:
\[-45^{\circ} +360^{\circ} =315^{\circ}\nonumber\]
Exercise \(\PageIndex{2}\)
Find an angle\(\beta\) coterminal with \(-300^{\circ}\) where \(0^{\circ} \le \beta <360^{\circ}\).
- Answer
-
\[\beta =-300+360=60^{\circ}\nonumber\]
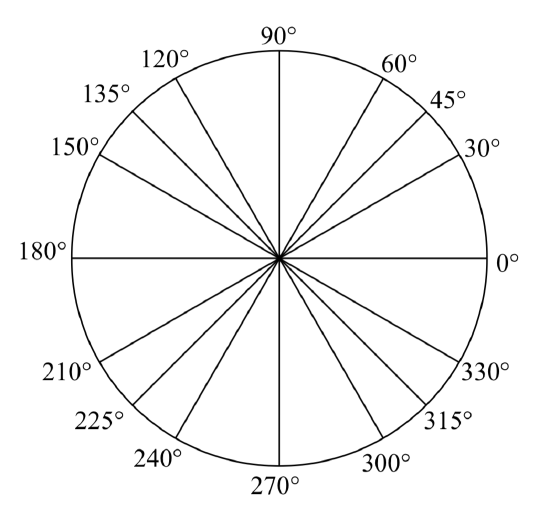 It can be helpful to have a familiarity with the frequently encountered angles in one rotation of a circle. It is common to encounter multiples of 30, 45, 60, and 90 degrees. These values are shown to the right. Memorizing these angles and understanding their properties will be very useful as we study the properties associated with angles
It can be helpful to have a familiarity with the frequently encountered angles in one rotation of a circle. It is common to encounter multiples of 30, 45, 60, and 90 degrees. These values are shown to the right. Memorizing these angles and understanding their properties will be very useful as we study the properties associated with angles
Angles in Radians
While measuring angles in degrees may be familiar, doing so often complicates matters since the units of measure can get in the way of calculations. For this reason, another measure of angles is commonly used. This measure is based on the distance around a circle.
Definition: arclength
Arclen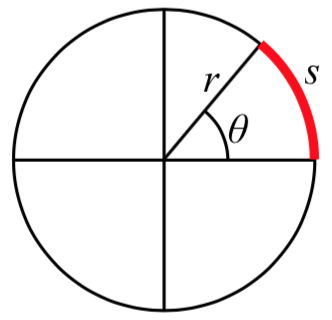 gth is the length of an arc, \(s\), along a circle of radius \(r\) subtended (drawn out) by an angle \(\theta\).
gth is the length of an arc, \(s\), along a circle of radius \(r\) subtended (drawn out) by an angle \(\theta\).
It is the portion of the circumference between the initial and terminal sides of the angle.
The length of the arc around an entire circle is called the circumference of a circle. The circumference of a circle is \(C=2\pi r\). The ratio of the circumference to the radius, produces the constant \(2\pi\). Regardless of the radius, this ratio is always the same, just as how the degree measure of an angle is independent of the radius.
To elaborate on this idea, consider two circles, one with radius 2 and one with radius 3. Recall the circumference (perimeter) of a circle is \(C=2\pi r\), where \(r\) is the radius of the circle. The smaller circle then has circumference \(2\pi (2)=4\pi\) and the larger has circumference\(2\pi (3)=6\pi\).
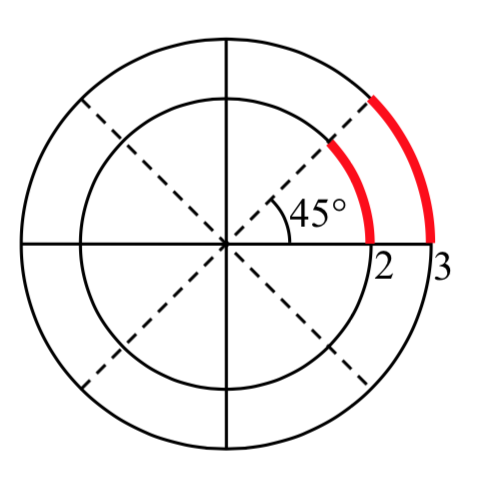 Drawing a 45 degree angle on the two circles, we might be interested in the length of the arc of the circle that the angle indicates. In both cases, the 45 degree angle draws out an arc that is \({1/8}^{th}\) of the full circumference, so for the smaller circle, the arclength = \(\dfrac{1}{8} (4\pi )=\dfrac{1}{2} \pi\), and for the larger circle, the length of the arc or arclength = \(\dfrac{1}{8} (6\pi )=\dfrac{3}{4} \pi\).
Drawing a 45 degree angle on the two circles, we might be interested in the length of the arc of the circle that the angle indicates. In both cases, the 45 degree angle draws out an arc that is \({1/8}^{th}\) of the full circumference, so for the smaller circle, the arclength = \(\dfrac{1}{8} (4\pi )=\dfrac{1}{2} \pi\), and for the larger circle, the length of the arc or arclength = \(\dfrac{1}{8} (6\pi )=\dfrac{3}{4} \pi\).
Notice what happens if we find the ratio of the arclength divided by the radius of the circle:
Smaller circle: \(\dfrac{\dfrac{1}{2} \pi }{2} =\dfrac{1}{4} \pi\)
Larger circle: \(\dfrac{\dfrac{3}{4} \pi }{3} =\dfrac{1}{4} \pi\)
The ratio is the same regardless of the radius of the circle – it only depends on the angle. This property allows us to define a measure of the angle based on arclength.
radians
The radian measure of an angle is the ratio of the length of the circular arc subtended by the angle to the radius of the circle.
In other words, if s is the length of an arc of a circle, and \(r\) is the radius of the circle, then
radian measure\(=\dfrac{s}{r}\)
If the circle has radius 1, then the radian measure corresponds to the length of the arc.
Because radian measure is the ratio of two lengths, it is a unitless measure. It is not necessary to write the label “radians” after a radian measure, and if you see an angle that is not labeled with “degrees” or the degree symbol, you should assume that it is a radian measure.
Considering the most basic case, the unit circle (a circle with radius 1), we know that 1 rotation equals 360 degrees, \(360^{\circ}\). We can also track one rotation around a circle by finding the circumference, \(C=2\pi r\), and for the unit circle \(C=2\pi\). These two different ways to rotate around a circle give us a way to convert from degrees to radians.
1 rotation = \(360{}^\circ\)=\(2\pi\) radians
1/2 rotation = \(180{}^\circ\) = \(\pi\) radians
1/4 rotation = \(90{}^\circ\)= \(\dfrac{\pi }{2}\) radians
Example \(\PageIndex{5}\)
Find the radian measure of one third of a full rotation.
Solution
For any circle, the arclength along such a rotation would be one third of the circumference, \(C=\dfrac{1}{3} (2\pi r)=\dfrac{2\pi r}{3}\). The radian measure would be the arclength divided by the radius:
\[\text{Radian measure} = \dfrac{2\pi r}{3r} =\dfrac{2\pi }{3}\]
converting between radians and degrees
1 degree = \(\dfrac{\pi }{180}\) radians
or: to convert from degrees to radians, multiply by \(\dfrac{\pi \text{radians}}{180^{\circ}}\)
1 radian = \(\dfrac{180}{\pi }\) degrees
or: to convert from radians to degrees, multiply by \(\dfrac{180^{\circ}}{\pi \text{radians}}\)
Converting Between Radians and Degrees
Example \(\PageIndex{6}\)
Convert \(\dfrac{\pi }{6}\) radians to degrees.
Solution
Since we are given a problem in radians and we want degrees, we multiply by \(\dfrac{180^{\circ}}{\pi }\).
Remember radians are a unitless measure, so we don’t need to write “radians.”
\(\dfrac{\pi }{6}\) radians = \(\dfrac{\pi }{6} \cdot \dfrac{180^{\circ}}{\pi } =30\) degrees.
Example \(\PageIndex{7}\)
Convert 15 degrees to radians.
Solution
In this example, we start with degrees and want radians so we use the other conversion\(\dfrac{\pi }{180^{\circ}}\)so that the degree units cancel and we are left with the unitless measure of radians.
15 degrees = \(15^{\circ} \cdot \dfrac{\pi }{180^{\circ}} =\dfrac{\pi }{12}\)
Exercise \(\PageIndex{3}\)
Convert \(\dfrac{7\pi }{10}\) radians to degrees.
- Answer
-
\[\dfrac{7\pi }{10} \cdot \dfrac{180^{\circ} }{\pi } =126^{\circ}\nonumber\]
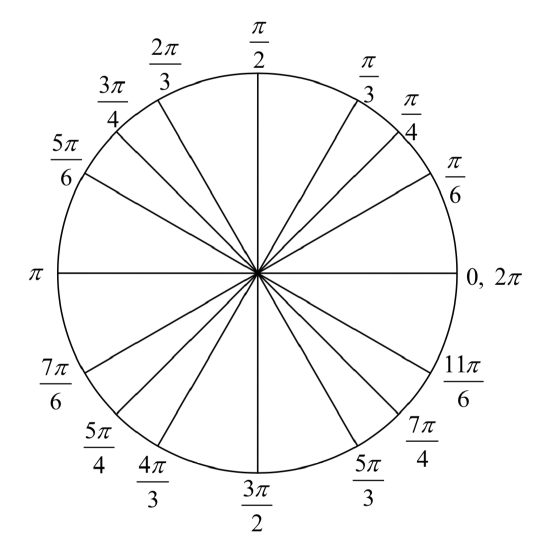 Just as we listed all the common angles in degrees on a circle, we should also list the corresponding radian values for the common measures of a circle corresponding to degree multiples of 30, 45, 60, and 90 degrees. As with the degree measurements, it would be advisable to commit these to memory.
Just as we listed all the common angles in degrees on a circle, we should also list the corresponding radian values for the common measures of a circle corresponding to degree multiples of 30, 45, 60, and 90 degrees. As with the degree measurements, it would be advisable to commit these to memory.
We can work with the radian measures of an angle the same way we work with degrees.
Example \(\PageIndex{8}\)
Find an angle \(\beta\) that is coterminal with \(\dfrac{19\pi }{4}\), where \(0\le \beta <2\pi\).
Solution
When working in degrees, we found coterminal angles by adding or subtracting 360 degrees, a full rotation. Likewise, in radians, we can find coterminal angles by adding or subtracting full rotations of \(2\pi\) radians.
\[\dfrac{19\pi }{4} -2\pi =\dfrac{19\pi }{4} -\dfrac{8\pi }{4} =\dfrac{11\pi }{4}\nonumber\]
The angle\(\dfrac{11\pi }{4}\) is coterminal, but not less than \(2\pi\), so we subtract another rotation.
\[\dfrac{11\pi }{4} -2\pi =\dfrac{11\pi }{4} -\dfrac{8\pi }{4} =\dfrac{3\pi }{4}\nonumber\]
The angle \(\dfrac{3\pi }{4}\) is coterminal with \(\dfrac{19\pi }{4}\).
Exercise \(\PageIndex{4}\)
Find an angle \(\phi\)that is coterminal with \(-\dfrac{17\pi }{6}\) where \(0\le \phi <2\pi\).
- Answer
-
\[-\dfrac{17\pi }{6} +2\pi +2\pi =-\dfrac{17\pi }{6} +\dfrac{12\pi }{6} +\dfrac{12\pi }{6} =\dfrac{7\pi }{6}\nonumber\]
Arclength and Area of a Sector
Recall that the radian measure of an angle was defined as the ratio of the arclength of a circular arc to the radius of the circle, \(\theta =\dfrac{s}{r}\). From this relationship, we can find arclength along a circle given an angle.
arclength on a circle
The length of an arc, \(s\), along a circle of radius \(r\) subtended by angle \(\theta\) in radians is
\[s=r\theta\]
Example \(\PageIndex{9}\)
Mercury orbits the sun at a distance of approximately 36 million miles. In one Earth day, it completes 0.0114 rotation around the sun. If the orbit was perfectly circular, what distance through space would Mercury travel in one Earth day?
Solution
To begin, we will need to convert the decimal rotation value to a radian measure.
Since one rotation = \(2\pi\) radians,
0.0114 rotation = \(2\pi (0.0114)=0.0716\) radians.
Combining this with the given radius of 36 million miles, we can find the arclength:
\(s=(36)(0.0716)=2.578\) million miles traveled through space.
Exercise \(\PageIndex{5}\)
Find the arclength along a circle of radius 10 subtended by an angle of 215 degrees.
- Answer
-
215\(^{\circ}\) = \(\dfrac{215\pi }{180}\) radians. \(s=10\cdot \dfrac{215\pi }{180} =\dfrac{215\pi }{18} \approx 37.525\)
In addition to arclength, we can also use angles to find the area of a sector of a circle. A sector is a portion of a circle contained between two lines from the center, like a slice of pizza or pie.
Recall that the area of a circle with radius \(r\) can be found using the formula \(A=\pi r^{2}\). If a sector is cut out by an angle of \(\theta\), measured in radians, then the fraction of full circle that angle has cut out is \(\dfrac{\theta }{2\pi }\), since \(2\pi\) is one full rotation. Thus, the area of the sector would be this fraction of the whole area:
\[\text{Area of sector}=\left(\dfrac{\theta }{2\pi } \right)\pi r^{2} =\dfrac{\theta \pi r^{2} }{2\pi } =\dfrac{1}{2} \theta r^{2}\nonumber\]
Definition: area of a sector
The area of a sector of a circle w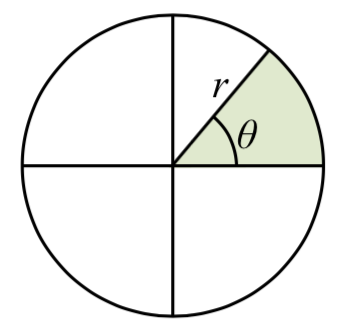 ith radius \(r\) subtended by an angle \(\theta\), measured in radians, is
ith radius \(r\) subtended by an angle \(\theta\), measured in radians, is
\[\text{Area of sector}=\dfrac{1}{2} \theta r^{2}\]
Example \(\PageIndex{10}\)
An automatic lawn sprinkler sprays a distance of 20 feet while rotating 30 degrees. What is the area of the sector of grass the sprinkler waters?
Solution
First, we need to convert the angle measure into radians. Since 30 degrees is one of our common angles, you ideally should already know the equivalent radian measure, but if not we can convert: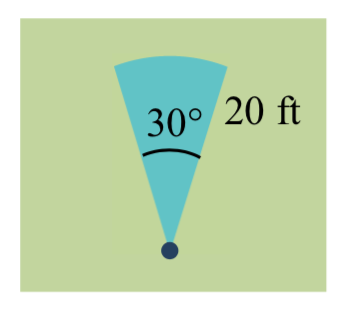
30 degrees = \(30 \cdot \dfrac{\pi }{180} =\dfrac{\pi }{6}\) radians.
The area of the sector is then Area \(=\dfrac{1}{2} \left(\dfrac{\pi }{6} \right)(20)^{2} =104.72\) ft\({}^{2}\)
Exercise \(\PageIndex{6}\)
In central pivot irrigation, a large irrigation pipe on wheels rotates around a center point, as pictured here (http://commons.wikimedia.org/wiki/Fi..._otech_002.JPG CC-BY-SA). A farmer has a central pivot system with a radius of 400 meters. If water restrictions only allow her to water 150 thousand square meters a day, what angle should she set the system to cover?

- Answer
-
\(\dfrac{1}{2} \theta (400)^{2} =150,000\). \(\theta =1.875\), or \(107.43^{\circ}\)
Linear and Angular Velocity
When your car drives down a road, it makes sense to describe its speed in terms of miles per hour or meters per second. These are measures of speed along a line, also called linear velocity. When a point on a circle rotates, we would describe its angular velocity, or rotational speed, in radians per second, rotations per minute, or degrees per hour.
Definition: angular and linear velocity
As a point moves along a circle of radius \(r\), its angular velocity, \(\omega\), can be found as the angular rotation \(\theta\) per unit time, \(t\).
\[\omega =\dfrac{\theta }{t}\]
The linear velocity, \(v\), of the point can be found as the distance traveled, arclength \(s\), per unit time, \(t\).
\[v=\dfrac{s}{t}\]
Example \(\PageIndex{11}\)
A water wheel completes 1 rotation every 5 seconds.  Find the angular velocity in radians per second. (http://en.Wikipedia.org/wiki/File:R%...m%C3%BChle.svg CC-BY)
Find the angular velocity in radians per second. (http://en.Wikipedia.org/wiki/File:R%...m%C3%BChle.svg CC-BY)
Solution
The wheel completes 1 rotation = \(2\pi\) radians in 5 seconds, so the angular velocity would be \(\omega =\dfrac{2\pi }{5} \approx 1.257\)radians per second.
Combining the definitions above with the arclength equation, \(s=r\theta\), we can find a relationship between angular and linear velocities. The angular velocity equation can be solved for \(\theta\), giving \(\theta =\omega t\). Substituting this into the arclength equation gives \(s=r\theta =r\omega t\).
Substituting this into the linear velocity equation gives
\(v=\dfrac{s}{t} =\dfrac{r\omega t}{t} =r\omega\)
relationship between linear and angular velocity
When the angular velocity is measured in radians per unit time, linear velocity and angular velocity are related by the equation
\[v=r\omega\]
Example \(\PageIndex{12}\)
A bicycle has wheels 28 inches in diameter. A tachometer determines the wheels are rotating at 180 RPM (revolutions per minute). Find the speed the bicycle is traveling down the road.
Solution
Here we have an angular velocity and need to find the corresponding linear velocity, since the linear speed of the outside of the tires is the speed at which the bicycle travels down the road.
We begin by converting from rotations per minute to radians per minute. It can be helpful to utilize the units to make this conversion
\[180\dfrac{\text{rotations}}{\text{minute}} \cdot \dfrac{2\pi \text{radians}}{\text{rotation}} =360\pi \dfrac{\text{radians}}{\text{minute}}\nonumber\]
Using the formula from above along with the radius of the wheels, we can find the linear velocity
\[v=(14 \text{inches})\left(360\pi \dfrac{\text{radians}}{\text{minute}} \right)=5040\pi \dfrac{\text{inches}}{\text{minute}}\nonumber\]
You may be wondering where the “radians” went in this last equation. Remember that radians are a unitless measure, so it is not necessary to include them.
Finally, we may wish to convert this linear velocity into a more familiar measurement, like miles per hour.
\[5040\pi \dfrac{\text{inches}}{\text{minute}} \cdot \dfrac{1 \text{feet}}{12 \text{inches}} \cdot \dfrac{1 \text{mile}}{5280 \text{feet}} \cdot \dfrac{60 \text{minutes}}{1 \text{hour}} =14.99\text{ miles per hour (mph)}\nonumber\]
Exercise \(\PageIndex{7}\)
A satellite is rotating around the earth at 27,934 kilometers per minute at an altitude of 242 km above the earth. If the radius of the earth is 6378 kilometers, find the angular velocity of the satellite.
- Answer
-
\(v\) = 27934. \(r\) = 6378+242=6620. \(\omega =\dfrac{v}{r} =\dfrac{27934}{6620} =4.2196\) radians per hour.
Important Topics of This Section
- Degree measure of angle
- Radian measure of angle
- Conversion between degrees and radians
- Common angles in degrees and radians
- Coterminal angles
- Arclength
- Area of a sector
- Linear and angular velocity


