9.1: Ellipses
- Page ID
- 13882
The National Statuary Hall in Washington, D.C. is an oval-shaped room called a whispering chamber because the shape makes it possible for sound to reflect from the walls in a special way. Two people standing in specific places are able to hear each other whispering even though they are far apart. To determine where they should stand, we will need to better understand ellipses.

Photo by Gary Palmer, Flickr, CC-BY, https://www.flickr.com/photos/gregpalmer/2157517950
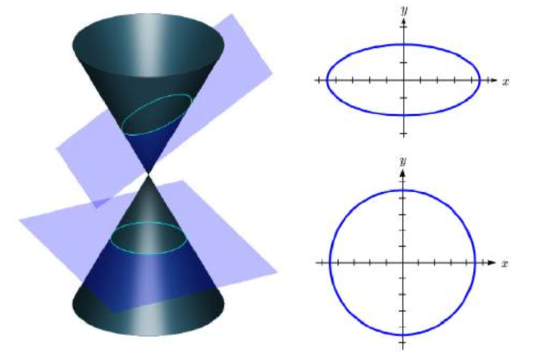
An ellipse is a type of conic section, a shape resulting from intersecting a plane with a cone and looking at the curve where they intersect. They were discovered by the Greek mathematician Menaechmus over two millennia ago.
The figure below (Pbroks13 (commons.wikimedia.org/wiki/F...with_plane.svg), “Conic sections with plane”, cropped to show only ellipse and circle by L Michaels, CC BY 3.0) shows two types of conic sections. When a plane is perpendicular to the axis of the cone, the shape of the intersection is a circle. A slightly titled plane creates an oval-shaped conic section called an ellipse.
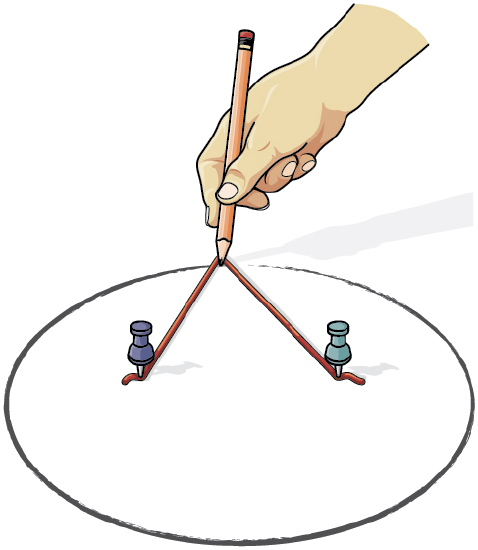
An ellipse can be drawn by placing two thumbtacks in a piece of cardboard then cutting a piece of string longer than the distance between the thumbtacks. Tack each end of the string to the cardboard, and trace a curve with a pencil held taught against the string. An ellipse is the set of all points where the sum of the distances from two fixed points is constant. The length of the string is the constant, and the two thumbtacks are the fixed points, called foci.
Definition: ELLIPSE Definition AND VOCABULARY
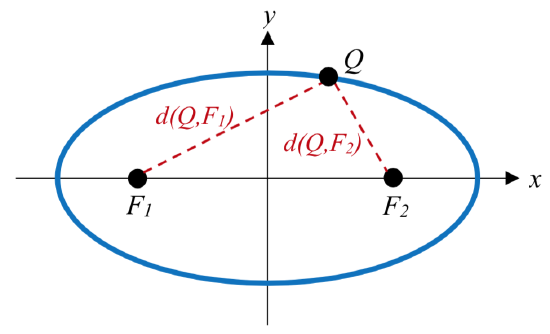
An ellipse is the set of all points \(\;Q\left( {x,y} \right)\) for which the sum of the distance to two fixed points \(F_1 \left( x_1,y_1 \right)\) and \(F_2 \left( x_2,y_2 \right)\), called the foci (plural of focus), is a constant k: \[d\left( {Q,{F_1}} \right) + d\left( {Q,{F_2}} \right) = k\]
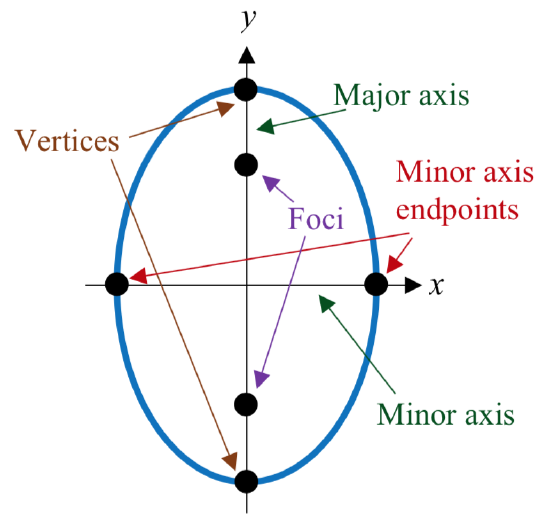
- The major axis is the line passing through the foci.
- Vertices are the points on the ellipse which intersect the major axis.
- The major axis length is the length of the line segment between the vertices.
- The center is the midpoint between the vertices (or the midpoint between the foci).
- The minor axis is the line perpendicular to the minor axis passing through the center.
- Minor axis endpoints are the points on the ellipse which intersect the minor axis.
- The minor axis endpoints are also sometimes called co-vertices.
- The minor axis length is the length of the line segment between minor axis endpoints.
Note that which axis is major and which is minor will depend on the orientation of the ellipse. In the ellipse shown at right, the foci lie on the \(y\) axis, so that is the major axis, and the \(x\) axis is the minor axis. Because of this, the vertices are the endpoints of the ellipse on the \(y\) axis, and the minor axis endpoints (co-vertices) are the endpoints on the \(x\) axis.
Ellipses Centered at the Origin
From the definition above we can find an equation for an ellipse. We will find it for a ellipse centered at the origin \(C\left( {0,0} \right)\) with foci at \({F_1}\left( {c,0} \right)\) and \({F_2}\left( { - c,0} \right)\) where \(c > 0\).
Suppose\(\;Q\left( {x,y} \right)\) is some point on the ellipse. The distance from \(F_1\) to \(Q\) is
\[d\left( Q,{F_1} \right) = \sqrt {{{\left( {x - c} \right)}^2} + {{\left( {y - 0} \right)}^2}\;} = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}\;} \nonumber\]
Likewise, the distance from \(F_2\) to \(Q\) is
\[d\left( {Q,{F_2}} \right) = \sqrt {{\left( {x - \left( { - c} \right)} \right)}^2 + {\left( {y - 0} \right)}^2} = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}\;} \nonumber\]
From the definition of the ellipse, the sum of these distances should be constant:
\[d\left( {Q,{F_1}} \right) + d\left( {Q,{F_2}} \right) = k\nonumber\]so that
\[\sqrt {\left( {x - c} \right)^2} + y^2; + \sqrt {{{\left( {x + c} \right)}^2} + {y^2}\;} = k\nonumber\]
If we label one of the vertices \(\left( a,0 \right)\), it should satisfy the equation above since it is a point on the ellipse. This allows us to write \(k\) in terms of \(a\).
\[\sqrt {\left( a - c \right)^2 +0^2} + \sqrt {\left( a + c \right)^2 + 0^2} = k\nonumber\]
\[\left| {a - c} \right| + \left| {a + c} \right| = k\nonumber\] Since \(a > c\), these will be positive
\[(a - c) + (a + c) = k\nonumber\]
\[2a = k\nonumber\]
Substituting that into our equation, we will now try to rewrite the equation in a friendlier form.
\[\sqrt {\left( x - c \right)^2 + y^2} + \sqrt {\left( x + c \right)^2 + y^2} = 2a\nonumber\]Move one radical
\[\sqrt {\left( x - c \right)^2 + y^2} = 2a - \sqrt {\left( x + c \right)^2 + y^2} \nonumber\]Square both sides
\[\left( \sqrt {\left( x - c \right)^2 + y^2 } \right)^2 = \left( 2a - \sqrt {\left( x + c \right)^2 + y^2} \right)^2\nonumber\]Expand
\[\left( x - c \right)^2 + y^2= 4a^2 - 4a\sqrt {\left( x + c \right)^2 + y^2} + \left( x + c \right)^2 + y^2\nonumber\]Expand more
\[x^2 - 2xc + c^2 + y^2 = 4a^2 - 4a\sqrt {\left( x + c \right)^2 + y^2} + x^2 + 2xc + c^2 + y^2\nonumber\]
Combining like terms and isolating the radical leaves
\[4a\sqrt {\left( x + c \right)^2 + y^2} = 4a^2 + 4xc\nonumber\]Divide by 4
\[a\sqrt {\left( x + c \right)^2 + y^2} = a^2 + xc\nonumber\]Square both sides again
\[a^2\left( \left( x + c \right)^2 + y^2 \right) = a^4 + 2a^2xc + x^2c^2\nonumber\]Expand
\[a^2\left( x^2 + 2xc + c^2 + y^2 \right) = a^4 + 2a^2xc + x^2c^2\nonumber\]Distribute
\[a^2x^2 + 2a^2xc + a^2c^2 + a^2y^2 = a^4 + 2a^2xc + x^2c^2\nonumber\]Combine like terms
\[a^2x^2 - x^2c^2 + a^2y^2 =a^4 - a^2c^2\nonumber\]Factor common terms
\[\left( a^2 - c^2 \right)x^2 + a^2y^2 = a^2\left( a^2 - c^2 \right)\nonumber\]
Let \(b^2 = a^2 - c^2\). Since \(a > c\), we know \(b > 0\). Substituting \(b^2\)for \(a^2 - c^2\) leaves
\[b^2x^2 + a^2y^2 = a^2b^2\nonumber\] Divide both sides by \(a^2b^2\)
\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\nonumber\]
This is the standard equation for an ellipse. We typically swap \(a\) and \(b\) when the major axis of the ellipse is vertical.
Definition: EQUATION OF AN ELLIPSE CENTERED AT THE ORIGIN IN STANDARD FORM
The standard form of an equation of an ellipse centered at the origin \(C\left( 0,0 \right)\) depends on whether the major axis is horizontal or vertical. The table below gives the standard equation, vertices, minor axis endpoints, foci, and graph for each.
| Major Axis | Horizontal | Vertical |
| Vertices | \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) | \(\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1\) |
| Standard Equation | (-\(a\), 0) and (\(a\), 0) | (0, -\(a\)) and (0, \(a\)) |
| Minor Axis Endpoints | (0, -\(b\)) and (0, \(b\)) | (-\(b\), 0) and (\(b\), 0) |
| Foci |
(-\(c\), 0) and (\(c\), 0) where \(b^2 = a^2 - c^2\) |
(0, -\(c\)) and (0, \(c\)) where \(b^2 = a^2 - c^2\) |
| Graph | 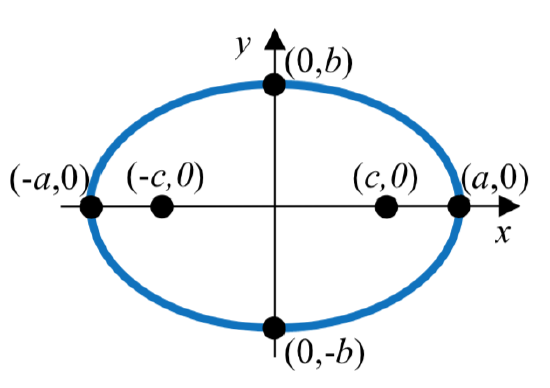 |
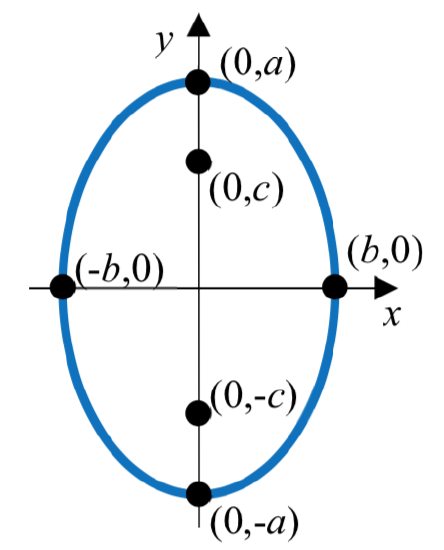 |
Example \(\PageIndex{1}\)
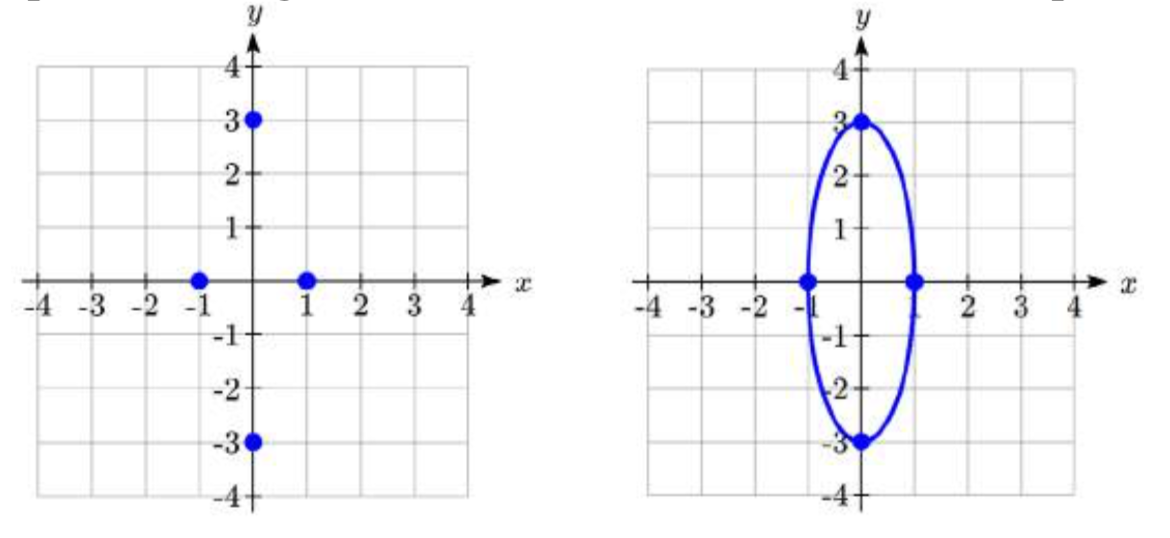
Put the equation of the ellipse \(9{x^2} + {y^2} = 9\) in standard form. Find the vertices, minor axis endpoints, length of the major axis, and length of the minor axis. Sketch the graph, then check using a graphing utility.
Solution
The standard equation has a 1 on the right side, so this equation can be put in standard form by dividing by 9:
\[\dfrac{x^2}{1} + \dfrac{y^2}{9} = 1\nonumber\]
Since the \(y\)-denominator is greater than the \(x\)-denominator, the ellipse has a vertical major axis. Comparing to the general standard form equation \(\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1\), we see the value of \(a = \sqrt 9 = 3\) and the value of \(b = \sqrt 1 = 1\).
- The vertices lie on the \(y\)-axis at (0, \(\pm a\)) = (0, \(\pm 3\)).
- The minor axis endpoints lie on the \(x\)-axis at (\(\pm b\), 0) = (\(\pm 1\), 0).
- The length of the major axis is \(2\left( a \right) = 2\left( 3 \right) = 6\).
- The length of the minor axis is \(2\left( b \right) = 2\left( 1 \right) = 2\).
To sketch the graph we plot the vertices and the minor axis endpoints. Then we sketch the ellipse, rounding at the vertices and the minor axis endpoints.
To check on a graphing utility, we must solve the equation for \(y\). Isolating \(y^2\) gives us
\[y^2 = 9\left( 1 - x^2 \right)\nonumber\]
Taking the square root of both sides we get
\[y = \pm 3\sqrt {1 - x^2} \nonumber\]
Under Y= on your graphing utility enter the two halves of the ellipse as \(y = 3\sqrt {1 - x^2} \) and \(y = - 3\sqrt {1 - x^2} \). Set the window to a comparable scale to the sketch with xmin = -5, xmax = 5, ymin= -5, and ymax = 5.
Here’s an example output on a TI-84 calculator:
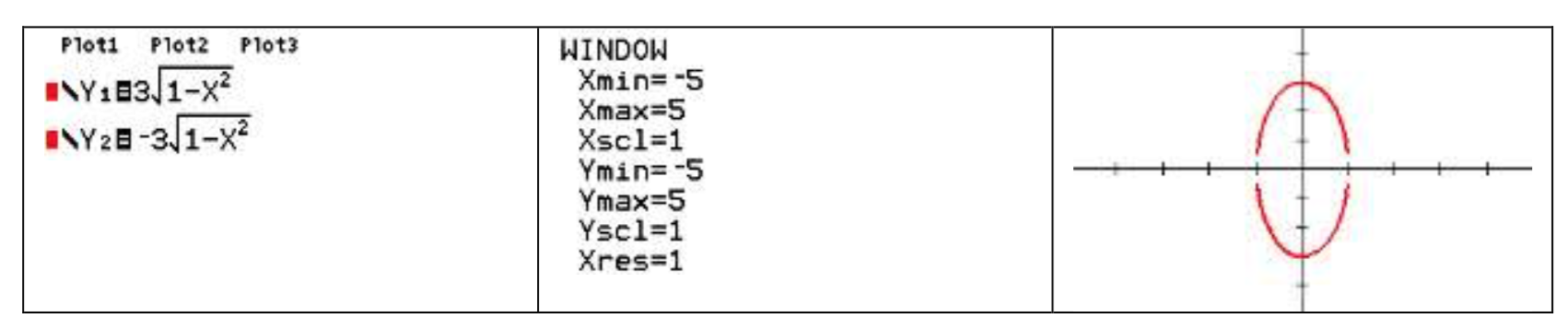
Sometimes we are given the equation. Sometimes we need to find the equation from a graph or other information.
Example \(\PageIndex{2}\)
Find the standard form of the equation for an ellipse centered at (0,0) with horizontal major axis length 28 and minor axis length 16.
Solution
Since the center is at (0,0) and the major axis is horizontal, the ellipse equation has the standard form \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\). The major axis has length \(2a = 28\) or \(a = 14\). The minor axis has length \(2b = 16\) or b = 8. Substituting gives \[\dfrac{x^2}{16^2} + \dfrac{y^2}{8^2} = 1\text{ or }\dfrac{x^2}{256} + \dfrac{y^2}{64.} = 1\nonumber\]
Exercise \(\PageIndex{1}\)
Find the standard form of the equation for an ellipse with horizontal major axis length 20 and minor axis length 6.
- Answer
-
\(2a = 20\), so \(a =10\). \(2b = 6\), so \(b = 3\). \[\dfrac{x^2}{100} + \dfrac{y^2}{9} = 1\nonumber\]
Example \(\PageIndex{3}\)
Find the standard form of the equation for the ellipse graphed here.
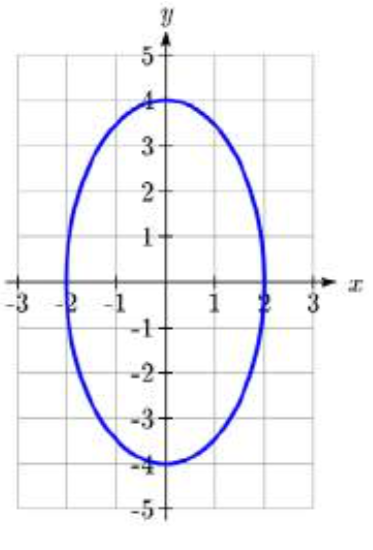
Solution
The center is at (0,0) and the major axis is vertical, so the standard form of the equation will be \(\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1\).
From the graph we can see the vertices are (0,4) and (0,-4), giving \(a = 4\).
The minor-axis endpoints are (2,0) and (-2,0), giving \(b = 2\).
The equation will be \[\dfrac{x^2}{2^2} + \dfrac{y^2}{4^2} = 1\text{ or }\dfrac{x^2}{4} + \dfrac{y^2}{16} = 1\nonumber\]
Ellipses Not Centered at the Origin
Not all ellipses are centered at the origin. The graph of such an ellipse is a shift of the graph centered at the origin, so the standard equation for one centered at (\(h\), \(k\)) is slightly different. We can shift the graph right \(h\) units and up \(k\) units by replacing \(x\) with \(x – h\) and \(y\) with \(y – k\), similar to what we did when we learned transformations.
Definition: EQUATION OF AN ELLIPSE CENTERED AT \((h,k)\) IN STANDARD FORM
The standard form of an equation of an ellipse centered at the point C\(\left( {h,k} \right)\) depends on whether the major axis is horizontal or vertical. The table below gives the standard equation, vertices, minor axis endpoints, foci, and graph for each.
| Major Axis | Horizontal | Vertical |
| Standard Equation | \(\dfrac{(x - h)^2}{a^2} + \dfrac{(y - k)^2}{b^2} = 1\) | \(\dfrac{(x - h)^2}{b^2} + \dfrac{(y - k)^2}{a^2} = 1\) |
| Vertices | \((h \pm a, k)\) | \((h, k \pm a)\) |
| Minor Axis Endpoints | \((h, k \pm b)\) | \((h \pm b, k)\) |
| Foci | \((h \pm c, k)\) where \(b^2 = a^2 - c^2\) |
\((h, k \pm c)\) where \(b^2 = a^2 - c^2\) |
| Graph | 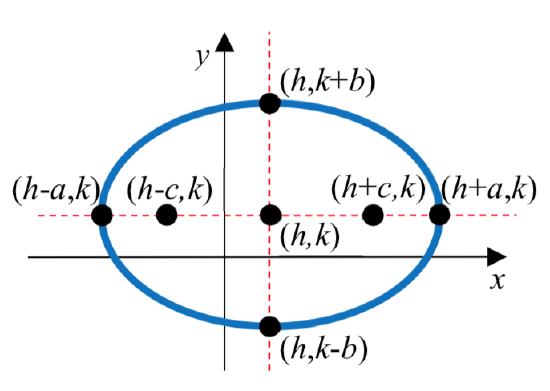 |
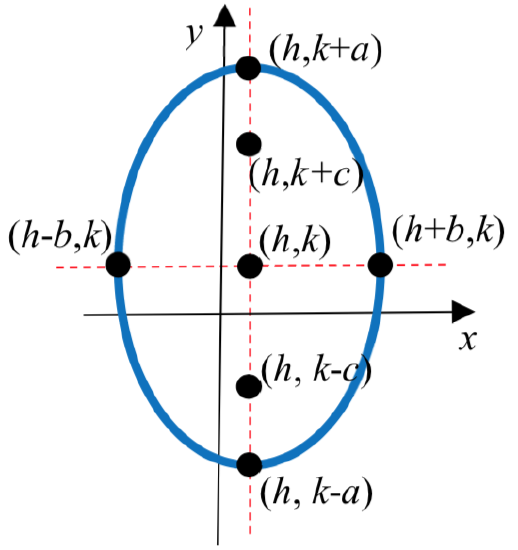 |
Example \(\PageIndex{4}\)
Put the equation of the ellipse \(x^2 + 2x + 4y^2 - 24y = - 33\) in standard form. Find the vertices, minor axis endpoints, length of the major axis, and length of the minor axis. Sketch the graph.
Solution
To rewrite this in standard form, we will need to complete the square, twice.
Looking at the \(x\) terms, \(x^2 + 2x\), we like to have something of the form \((x + n)^2\). Notice that if we were to expand this, we’d get \(x^2 + 2nx + n^2\), so in order for the coefficient on \(x\) to match, we’ll need \((x + 1)^2 = x^2 + 2x + 1\). However, we don’t have \(a +1\) on the left side of the equation to allow this factoring. To accommodate this, we will add 1 to both sides of the equation, which then allows us to factor the left side as a perfect square:
\[x^2 + 2x + 1 + 4y^2 - 24y = - 33 + 1\nonumber\]
\[(x + 1)^2 + 4y^2 - 24y = - 32\nonumber\]
Repeating the same approach with the \(y\) terms, first we’ll factor out the 4.
\[4y^2 - 24y = 4(y^2 - 6y)\nonumber\]
Now we want to be able to write \(4\left( y^2 - 6y \right)\) as
\[4(y + n)^2 = 4\left( y^2 + 2ny + n^2 \right)\nonumber\]
For the coefficient of \(y\) to match, \(n\) will have to -3, giving \(4(y - 3)^2 = 4\left( y^2 - 6y + 9 \right) = 4y^2 - 24y + 36\).
To allow this factoring, we can add 36 to both sides of the equation.
\[(x + 1)^2 + 4y^2 - 24y + 36 = - 32 + 36\nonumber\]
\[(x + 1)^2 + 4\left( y^2 - 6y + 9 \right) = 4\nonumber\]
\[(x + 1)^2 + 4\left( y - 3 \right)^2 = 4\nonumber\]
Dividing by 4 gives the standard form of the equation for the ellipse
\[\dfrac{\left( x + 1 \right)^2}{4} + \dfrac{\left( y - 3 \right)^2}{1} = 1\nonumber\]
Since the \(x\)-denominator is greater than the \(y\)-denominator, the ellipse has a horizontal major axis. From the general standard equation \(\dfrac{\left( x - h \right)^2}{a^2} + \dfrac{\left( h - k \right)^2}{b^2} = 1\) we see the value of \(a = \sqrt 4 = 2\) and the value of \(b = \sqrt 1 = 1\).
The center is at (\(h\), \(k\)) = (-1, 3).
The vertices are at (\(h \pm a\), \(k\)) or (-3, 3) and (1,3).
The minor axis endpoints are at (\(h\), \(k \pm b\)) or (-1, 2) and (-1,4).
The length of the major axis is \(2\left( a \right) = 2\left( 2 \right) = 4\).
The length of the minor axis is \(2\left( b \right) = 2\left( 1 \right) = 2\).
To sketch the graph we plot the vertices and the minor axis endpoints. Then we sketch the ellipse, rounding at the vertices and the minor axis endpoints.
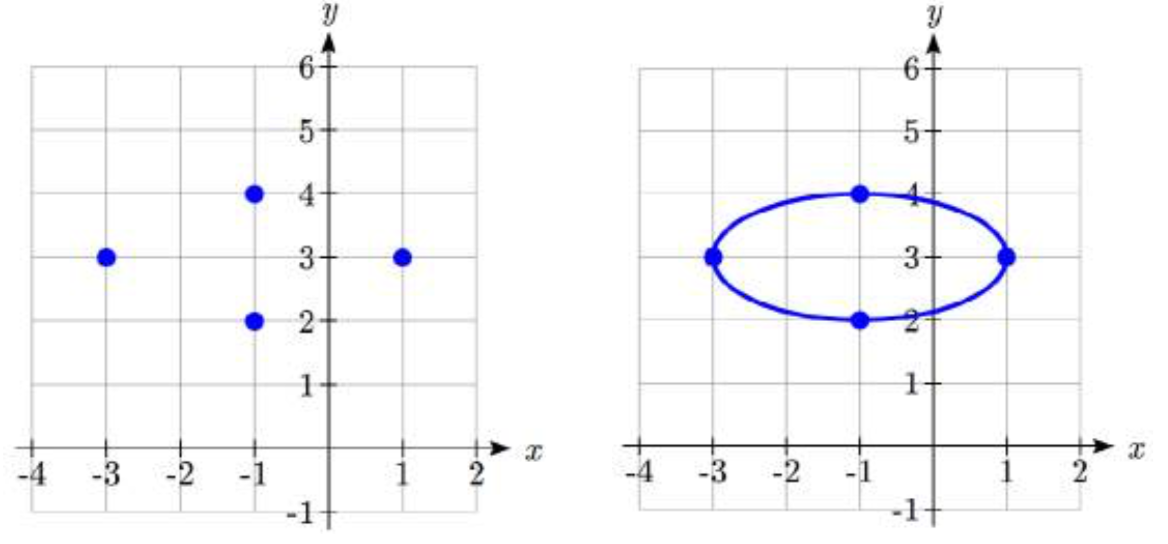
Example \(\PageIndex{5}\)
Find the standard form of the equation for an ellipse centered at (-2,1), a vertex at (-2,4) and passing through the point (0,1).
Solution
The center at (-2,1) and vertex at (-2,4) means the major axis is vertical since the x-values are the same. The ellipse equation has the standard form
\[\dfrac{\left( x - h \right)^2}{b^2} + \dfrac{\left( y - k \right)^2}{a^2} = 1\nonumber\]
The value of \(a = 4 - 1 = 3\). Substituting \(a = 3\), \(h = -2\), and \(k = 1\) gives
\[\dfrac{\left( x + 2 \right)^2}{b^2} + \dfrac{\left( y - 1 \right)^2}{3^2} = 1\nonumber\]Substituting for \(x\) and \(y\) using the point (0,1) gives
\[\dfrac{\left( 0 + 2 \right)^2}{b^2} + \dfrac{\left( 1 - 1 \right)^2}{3^2} = 1\nonumber\]
Solving for b gives \(b = 2\).
The equation of the ellipse in standard form is \[\dfrac{\left( x + 2 \right)^2}{2^2} + \dfrac{\left( y - 1 \right)^2}{3^2} = 1\text{ or }\dfrac{\left( x + 2 \right)^2}{4} + \dfrac{\left( y - 1 \right)^2}{9} = 1\nonumber\]
Exercise \(\PageIndex{2}\)
Find the center, vertices, minor axis endpoints, length of the major axis, and length of the minor axis for the ellipse \(\left( x - 4 \right)^2 + \dfrac{\left( y + 2 \right)^2}{4} = 1\).
- Answer
-
Center (4, -2). Vertical ellipse with \(a = 2\), \(b = 1\).
Vertices at (4, -2 \(\pm\) 2) = (4, 0) and (4, -4),
minor axis endpoints at (4 \(\pm\) 1, -2) = (3,-2) and (5,-2),
major axis length 4, minor axis length 2
Bridges with Semielliptical Arches
Arches have been used to build bridges for centuries, like in the Skerton Bridge in England which uses five semielliptical arches for support. Semielliptical arches can have engineering benefits such as allowing for longer spans between supports.

(Maxine Armstrong (commons.wikimedia.org/wiki/F...r,_England.JPG), “Skerton Bridge, Lancaster, England”, CC BY-SA)
Example \(\PageIndex{6}\)
A bridge over a river is supported by a single semielliptical arch. The river is 50 feet wide. At the center, the arch rises 20 feet above the river. The roadway is 4 feet above the center of the arch. What is the vertical distance between the roadway and the arch 15 feet from the center?
Solution
Put the center of the ellipse at (0,0) and make the span of the river the major axis.
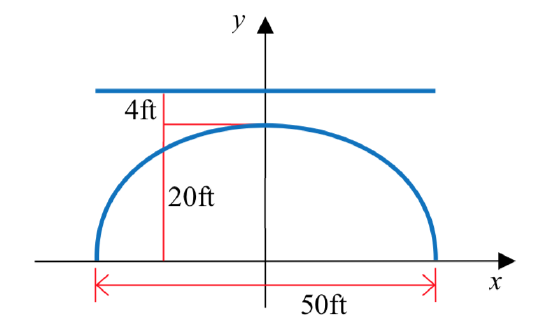
Since the major axis is horizontal, the equation has the form \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\).
The value of \(a = \dfrac{1}{2}(50) = 25\) and the value of \(b = 20\), giving \(\dfrac{x^2}{25^2} + \dfrac{y^2}{15^2} = 1\).
Substituting \(x = 15\) gives \(\dfrac{15^2}{25^2} + \dfrac{y^2}{20^2} = 1\). Solving for \(y\), \[y = 20\sqrt {1 - \dfrac{225}{625}} = 16\nonumber\]
The roadway is 20 + 4 = 24 feet above the river. The vertical distance between the roadway and the arch 15 feet from the center is 24 - 16 = 8 feet.
Ellipse Foci
The location of the foci can play a key role in ellipse application problems. Standing on a focus in a whispering gallery allows you to hear someone whispering at the other focus. To find the foci, we need to find the length from the center to the foci, \(c\), using the equation \({b^2} = {a^2} - {c^2}\). It looks similar to, but is not the same as, the Pythagorean Theorem.
Example \(\PageIndex{7}\)
The National Statuary Hall whispering chamber is an elliptical room 46 feet wide and 96 feet long. To hear each other whispering, two people need to stand at the foci of the ellipse. Where should they stand?
Solution
We could represent the hall with a horizontal ellipse centered at the origin. The major axis length would be 96 feet, so \(a = \dfrac{1}{2}(96) = 48\), and the minor axis length would be 46 feet, so \(b = \dfrac{1}{2}(46) = 23\). To find the foci, we can use the equation \(b^2 = a^2 - c^2\).
\[23^2 =48^2 - c^2\nonumber\]
\[c^2 = 48^2 - 23^2\nonumber\]
\[c = \sqrt {1775} \approx \pm 42\text{ ft}\nonumber\]
To hear each other whisper, two people would need to stand 2(42) = 84 feet apart along the major axis, each about 48 – 42 = 6 feet from the wall.
Example \(\PageIndex{8}\)
Find the foci of the ellipse \(\dfrac{\left( x - 2 \right)^2}{4} + \dfrac{\left( y + 3 \right)^2}{29} = 1\).
Solution
The ellipse is vertical with an equation of the form \(\dfrac{\left( x - h \right)^2}{b^2} + \dfrac{\left( y - k \right)^2}{a^2} = 1\).
The center is at (\(h\), \(k\)) = (2, -3). The foci are at (\(h\), \(k \pm c\)).
To find length \(c\) we use \(b^2 = a^2 - c^2\).
Substituting gives \(4 = 29 - c^2\) or \(c = \sqrt {25} = 5\).
The ellipse has foci (2, -3 ± 5), or (2, -8) and (2, 2).
Example \(\PageIndex{9}\)
Find the standard form of the equation for an ellipse with foci (-1,4) and (3,4) and major axis length 10.
Solution
Since the foci differ in the \(x\) -coordinates, the ellipse is horizontal with an equation of the form \(\dfrac{\left( x - h \right)^2}{a^2} + \dfrac{\left( h - k \right)^2}{b^2} = 1\).
The center is at the midpoint of the foci \(\left( \dfrac{x_1 + x_2}{2},\dfrac{y_1 + y_2}{2} \right) = \left( \dfrac{\left( - 1 \right) + 3}{2},\dfrac{4 + 4}{2} \right) = \left( 1,4 \right)\).
The value of \(a\) is half the major axis length: \[a = \dfrac{1}{2}(10) = 5\nonumber\]
The value of \(c\) is half the distance between the foci: \[c = \dfrac{1}{2}(3 - ( - 1)) = \dfrac{1}{2}(4) = 2\nonumber\]
To find length \(b\) we use \({b^2} = {a^2} - {c^2}\). Substituting a and c gives \(b^2 = 5^2 - 2^2\) = 21.
The equation of the ellipse in standard form is \[\dfrac{\left( x - 1 \right)^2}{5^2} + \dfrac{\left( y - 4 \right)^2}{21} = 1\text{ or }\dfrac{\left( x - 1 \right)^2}{25} + \dfrac{\left( y - 4 \right)^2}{21} = 1\nonumber\]
Exercise \(\PageIndex{3}\)
Find the standard form of the equation for an ellipse with focus (2,4), vertex (2,6), and center (2,1).
- Answer
-
Vertex, center, and focus have the same \(x\)-value, so it’s a vertical ellipse.
Using the vertex and center, \[a = 6 – 1 = 5\nonumber\]
Using the center and focus, \[c = 4 – 1 = 3\nonumber\]
\[b^2 = 5^2 - 3^2\quad b = 4\nonumber\]
\[\dfrac{\left( x - 2 \right)^2}{16} + \dfrac{\left( y - 1 \right)^2}{25} = 1\nonumber\]
Planetary Orbits
It was long thought that planetary orbits around the sun were circular. Around 1600, Johannes Kepler discovered they were really elliptical (Technically, they’re approximately elliptical. The orbits of the planets are not exactly elliptical because of interactions with each other and other celestial bodies.). His first law of planetary motion says that planets travel around the sun in an elliptical orbit with the sun as one of the foci. The length of the major axis can be found by measuring the planet’s aphelion, its greatest distance from the sun, and perihelion, its shortest distance from the sun, and summing them together.
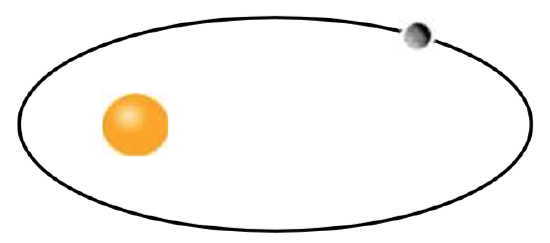
Example \(\PageIndex{10}\)
Mercury’s aphelion is 35.98 million miles and its perihelion is 28.58 million miles. Write an equation for Mercury’s orbit.
Solution
Let the center of the ellipse be (0,0) and its major axis be horizontal so the equation will have form \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\).
The length of the major axis is \(2a = 35.98 + 28.58 = 64.56\) giving \(a = 32.28\) and \(a^2 = 1041.9984\).
Since the perihelion is the distance from the focus to one vertex, we can find the distance between the foci by subtracting twice the perihelion from the major axis length: \(2c = 64.56 - 2\left( 28.58 \right) = 7.4\) giving \(c = 3.7\).
Substitution of \(a\) and \(c\) into \(b^2 = a^2 - c^2\) yields \(b^2 = 32.28^2 - 3.7^2 = 1028.3084\).
The equation is \[\dfrac{x^2}{1041.9984} + \dfrac{y^2}{1028.3084} = 1\nonumber\]
Important Topics of This Section
- Ellipse Definition
- Ellipse Equations in Standard Form
- Ellipse Foci
- Applications of Ellipses


