3.8: Inverses and Radical Functions
- Page ID
- 13848
In this section, we will explore the inverses of polynomial and rational functions, and in particular the radical functions that arise in the process.
Example \(\PageIndex{1}\)
A water runoff collector is built in the shape of a parabolic trough as shown below. Find the surface area of the water in the trough as a function of the depth of the water.
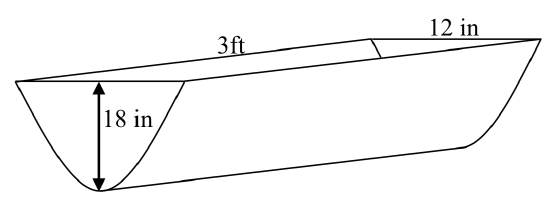
Solution
Since it will be helpful to have an equation for the parabolic cross-sectional shape, we will impose a coordinate system at the cross section, with \(x\) measured horizontally and \(y\) measured vertically, with the origin at the vertex of the parabola.
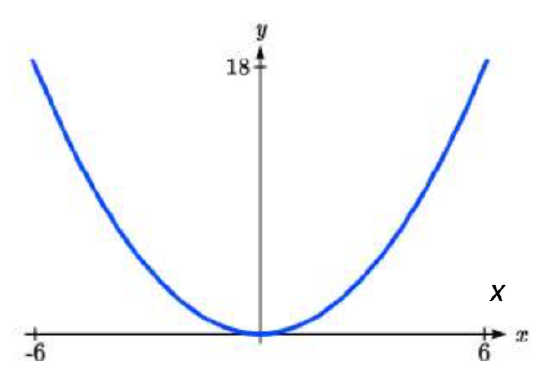
From this we find an equation for the parabolic shape. Since we placed the origin at the vertex of the parabola, we know the equation will have form \(y(x)=ax^{2}\). Our equation will need to pass through the point (6,18), from which we can solve for the stretch factor \(a\):
\[\begin{array}{l} {18=a6^{2} } \\ {a=\dfrac{18}{36} =\dfrac{1}{2} } \end{array}\nonumber \]
Our parabolic cross section has equation \(y(x)=\dfrac{1}{2} x^{2}\)
Since we are interested in the surface area of the water, we are interested in determining the width at the top of the water as a function of the water depth. For any depth \(y\) the width will be given by \(2x\), so we need to solve the equation above for \(x\). However notice that the original function is not one-to-one, and indeed given any output there are two inputs that produce the same output, one positive and one negative.
To find an inverse, we can restrict our original function to a limited domain on which it is one-to-one. In this case, it makes sense to restrict ourselves to positive x values. On this domain, we can find an inverse by solving for the input variable:
\[\begin{array}{l} {y=\dfrac{1}{2} x^{2} } \\ {2y=x^{2} } \end{array}\quad x=\pm \sqrt{2y}\nonumber \]
This is not a function as written. Since we are limiting ourselves to positive \(x\) values, we eliminate the negative solution, giving us the inverse function we’re looking for
\[x(y)=\sqrt{2y}\nonumber \]
Since \(x\) measures from the center out, the entire width of the water at the top will be \(2x\). Since the trough is 3 feet (36 inches) long, the surface area will then be 36(2x), or in terms of \(y\):
\[\text{Area}=72x=72\sqrt{2y}\nonumber\]
The previous example illustrated two important things:
- When finding the inverse of a quadratic, we have to limit ourselves to a domain on which the function is one-to-one.
- The inverse of a quadratic function is a square root function. Both are toolkit functions and different types of power functions.
Functions involving roots are often called radical functions.
Example \(\PageIndex{2}\)
Find the inverse of \(f(x)=(x-2)^{2} -3=x^{2} -4x+1\)
Solution
From the transformation form of the function, we can see this is a transformed quadratic with vertex at (2,-3) that opens upwards. Since the graph will be decreasing on one side of the vertex, and increasing on the other side, we can restrict this function to a domain on which it will be one-to-one by limiting the domain to\(x \ge 2\).
To find the inverse, we will use the vertex form of the quadratic. We start by replacing the \(f(x)\) with a simple variable \(y\), then solve for \(x\).
\[y=(x-2)^{2} -3\nonumber\] Add 3 to both sides
\[y+3=(x-2)^{2}\nonumber\] Take the square root
\[\pm \sqrt{y+3} =x-2\nonumber\] Add 2 to both sides
\[2\pm \sqrt{y+3} =x\nonumber \]
Of course, as written this is not a function. Since we restricted our original function to a domain of \(x\ge 2\), the outputs of the inverse should be the same, telling us to utilize the positive case:
\[x=f^{-1} (y)=2+\sqrt{y+3}\nonumber\]
If the quadratic had not been given in vertex form, rewriting it into vertex form is probably the best approach. Alternatively, we could have taken the standard equation and rewritten it equal to zero:
\[0=x^{2} -4x+1-y\nonumber\]
We would then be able to use the quadratic formula with \(a=1\), \(b=-4\), and \(c=(1-y)\), resulting in the same solutions we found above:
\[x=\dfrac{-(-4)\pm \sqrt{(-4)^{2} -4(1)(1-y)} }{2} =2\pm \dfrac{\sqrt{12+4y} }{2} =2\pm \sqrt{3+y}\nonumber \]
Exercise \(\PageIndex{1}\)
Find the inverse of the function \(f(x)=x^{2} +1\), on the domain \(x \ge 0\).
- Answer
-
\[y=x^{2} +1\nonumber\]
\[y-1=x^{2}\nonumber\]
\[x=f^{-1} (y)=\sqrt{y-1}\nonumber\]
While it is not possible to find an inverse of most polynomial functions, some other basic polynomials are invertible.
Example \(\PageIndex{3}\)
Find the inverse of the function \(f(x)=5x^{3} +1\).
Solution
This is a transformation of the basic cubic toolkit function, and based on our knowledge of that function, we know it is one-to-one. Solving for the inverse by solving for \(x\)
\[\begin{array}{l} {y=5x^{3} +1} \\ {y-1=5x^{3} } \\ {\dfrac{y-1}{5} =x^{3} } \\ {x=f^{-1} (y)=\sqrt[{3}]{\dfrac{y-1}{5} } } \end{array}\nonumber \]
Notice that this inverse is also a transformation of a power function with a fractional power, \(x^{1/3}\).
Exercise \(\PageIndex{2}\)
Which toolkit functions have inverse functions without restricting their domain?
- Answer
-
identity, cubic, square root, cube root
Besides being important as an inverse function, radical functions are common in important physical models.
Example \(\PageIndex{4}\)
The velocity, \(v\) in feet per second, of a car that slammed on its brakes can be determined based on the length of skid marks that the tires left on the ground. This relationship is given by
\[v(d)=\sqrt{2gfd} \nonumber\]
In this formula, \(g\) represents acceleration due to gravity (32 ft/sec\({}^{2}\)), d is the length of the skid marks in feet, and \(f\) is a constant representing the friction of the surface. A car lost control on wet asphalt, with a friction coefficient of 0.5, leaving 200 foot skid marks. How fast was the car travelling when it lost control?
Solution
Using the given values of \(f\) = 0.5 and \(d\) = 200, we can evaluate the given formula:
\(v(200)=\sqrt{2(32)(0.5)(200)} =80\) ft/sec, which is about 54.5 miles per hour.
When radical functions are composed with other functions, determining domain can become more complicated.
Example \(\PageIndex{5}\)
Find the domain of the function \(f(x)=\sqrt{\dfrac{(x+2)(x-3)}{(x-1)} }\).
Solution
Since a square root is only defined when the quantity under the radical is non-negative, we need to determine where \(\dfrac{(x+2)(x-3)}{(x-1)} \ge 0\). A rational function can change signs (change from positive to negative or vice versa) at horizontal intercepts and at vertical asymptotes. For this equation, the graph could change signs at \(x\) = -2, 1, and 3.
To determine on which intervals the rational expression is positive, we could evaluate the expression at test values, or sketch a graph. While both approaches work equally well, for this example we will use a graph.
This function has two horizontal intercepts, both of which exhibit linear behavior, where the graph will pass through the intercept. There is one vertical asymptote, corresponding to a linear factor, leading to a behavior similar to the basic reciprocal toolkit function. There is a vertical intercept at (0, 6). This graph does not have a horizontal asymptote, since the degree of the numerator is larger than the degree of the denominator.
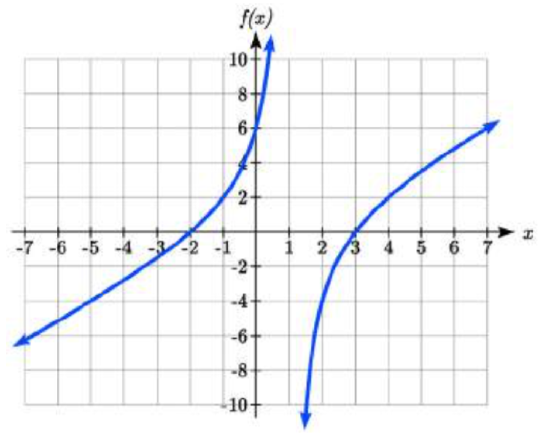 From the vertical intercept and horizontal intercept at \(x\) = -2, we can sketch the left side of the graph. From the behavior at the asymptote, we can sketch the right side of the graph.
From the vertical intercept and horizontal intercept at \(x\) = -2, we can sketch the left side of the graph. From the behavior at the asymptote, we can sketch the right side of the graph.
From the graph, we can now tell on which intervals this expression will be non-negative, so the original function \(f(x)\) will be defined.
\(f(x)\) has domain \(-2\le x<1\; or\; x\ge 3\), or in interval notation, \([-2,1)\bigcup [3,\infty )\).
Like with finding inverses of quadratic functions, it is sometimes desirable to find the inverse of a rational function, particularly of rational functions that are the ratio of linear functions, such as our concentration examples.
Example \(\PageIndex{6}\)
The function \(C(n)=\dfrac{20+0.4n}{100+n}\) was used in the previous section to represent the concentration of an acid solution after \(n\) mL of 40% solution has been added to 100 mL of a 20% solution. We might want to be able to determine instead how much 40% solution has been added based on the current concentration of the mixture.
Solution
To do this, we would want the inverse of this function:
\[C=\dfrac{20+0.4n}{100+n}\nonumber\] multiply both sides by the denominator
\[C(100+n)=20+0.4n\nonumber\] distribute
\[100C+Cn=20+0.4n\nonumber\] group everything with \(n\) on one side
\[100C-20=0.4n-Cn\nonumber\] factor out \(n\)
\[100C-20=(0.4-C)n\nonumber\] divide to find the inverse
\[n(C)=\dfrac{100C-20}{0.4-C}\nonumber\]
If, for example, we wanted to know how many mL of 40% solution need to be added to obtain a concentration of 35%, we can simply evaluate the inverse rather than solving an equation involving the original function:
\(n(0.35)=\dfrac{100(0.35)-20}{0.4-0.35} =\dfrac{15}{0.05} =300\) mL of 40% solution would need to be added.
Exercise \(\PageIndex{3}\)
Find the inverse of the function \(f(x)=\dfrac{x+3}{x-2}\).
- Answer
-
\[y=\dfrac{x+3}{x-2}\nonumber\]
\[y(x-2)=x+3\nonumber\]
\[yx-2y=x+3\nonumber\]
\[yx-x=2y+3\nonumber\]
\[x(y-1)=2y+3\nonumber\]
\[f^{-1} (y)=\dfrac{2y+3}{y-1}\nonumber\]
Important Topics of this Section
- Imposing a coordinate system
- Finding an inverse function
- Restricting the domain
- Invertible toolkit functions
- Radical Functions
- Inverses of rational functions


