5.5: Right Triangle Trigonometry
- Page ID
- 13862
In Section 5.3 we were introduced to the sine and cosine function as ratios of the sides of a triangle drawn inside a circle, and spent the rest of that section discussing the role of those functions in finding points on the circle. In this section, we return to the triangle, and explore the applications of the trigonometric functions to right triangles where circles may not be involved.
Recall that we defined sine and cosine as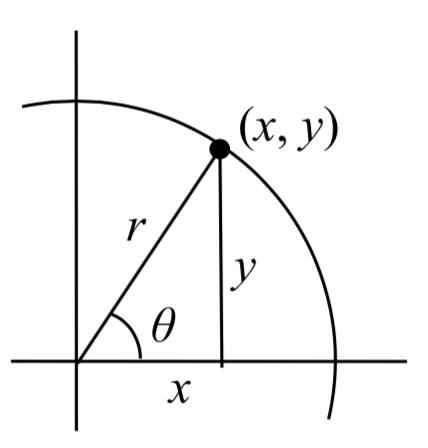
\[\sin (\theta ) = \dfrac{y}{r}\nonumber\]
\[\cos(\theta ) = \dfrac{x}{r}\nonumber\]
Separating the triangle from the circle, we can make equivalent but more general definitions of the sine, cosine, and tangent on a right triangle. On the right triangle, we will label the hypotenuse as well as the side opposite the angle and the side adjacent (next to) the angle.
RIGHT TRIANGLE RELATIONSHIPS
Given a right triangle with an angle of \(\theta\)
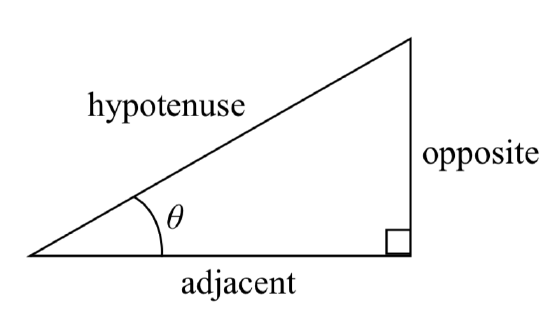
\[\text{sin} (\theta) = \dfrac{\text{opposite}}{\text{hypotenuse}}\]
\[\text{cos} (\theta) = \dfrac{\text{adjacent}}{\text{hypotenuse}}\]
\[\text{tan} (\theta) = \dfrac{\text{opposite}}{\text{adjacent}}\]
A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.”
Example \(\PageIndex{1}\)
\(\alpha\)\(\alpha\)Given the triangle shown, find the value for \(\text{cos}(\alpha)\).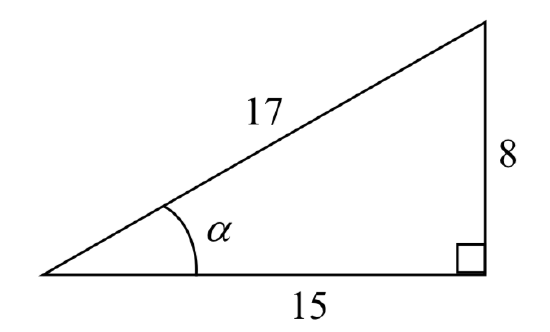
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so
\[\text{cos}(\alpha) = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{15}{17}\nonumber\]
When working with general right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the sine and cosine of either of the two acute angles in the triangle.
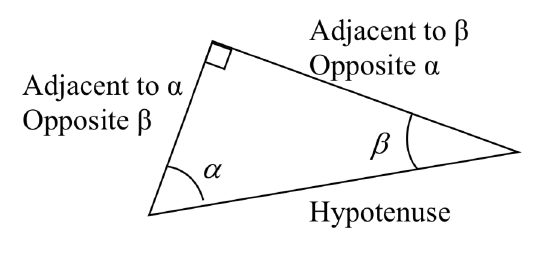
Example \(\PageIndex{2}\)
Using the triangle shown, evaluate cos(\(\alpha\)), sin(\(\alpha\)), cos(\(\beta\)), and sin(\(\beta\)),
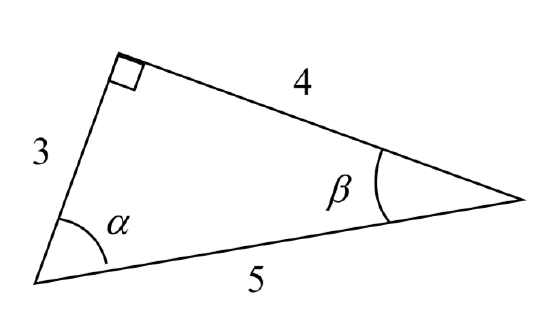
Solution
\[\text{cos}(\alpha) = \dfrac{\text{adjacent to } \alpha}{\text{hypotenuse}} = \dfrac{3}{5}\nonumber\]
\[\text{sin}(\alpha) = \dfrac{\text{opposite } \alpha}{\text{hypotenuse}} = \dfrac{4}{5}\nonumber\]
\[\text{cos}(\beta) = \dfrac{\text{adjacent to } \beta}{\text{hypotenuse}} = \dfrac{4}{5}\nonumber\]
\[\text{cos}(\beta) = \dfrac{\text{opposite } \beta}{\text{hypotenuse}} = \dfrac{3}{5}\nonumber\]
Exercise \(\PageIndex{1}\)
A right triangle is drawn with angle \(\alpha\) opposite a side with length 33, angle \(\beta\) opposite a side with length 56, and hypotenuse 65. Find the sine and cosine of \(\alpha\) and \(\beta\)
- Answer
-
\[\text{sin} (\alpha) = \frac{33}{65}\nonumber\]
\[\text{cos} (\alpha) = \frac{56}{65}\nonumber\]
\[\text{sin} (\beta) = \frac{56}{65}\nonumber\]
\[\text{cos} (\beta) = \frac{33}{65}\nonumber\]
You may have noticed that in the above example that \(\cos (\alpha )=\sin (\beta )\) and \(\cos (\beta )=\sin (\alpha )\). This makes sense since the side opposite \(\alpha\) is also adjacent to \(\beta\). Since the three angles in a triangle need to add to \(\pi\), or 180 degrees, then the other two angles must add to \(\dfrac{\pi }{2}\), or 90 degrees, so \(\beta =\dfrac{\pi }{2} -\alpha\), and \(\alpha =\dfrac{\pi }{2} -\beta\). Since \(\cos (\alpha )=\sin (\beta )\), then \(\cos (\alpha )=\sin \left(\dfrac{\pi }{2} -\alpha \right)\).
COFUNCTION IDENTITIES
The confunction identities for sine and cosine are:
\[\text{cos} (\theta) = \text{sin} (\dfrac{\pi}{2} - \theta)\]
\[\text{sin} (\theta) = \text{cos} (\dfrac{\pi}{2} - \theta)\]
In the previous examples, we evaluated the sine and cosine on triangles where we knew all three sides of the triangle. Right triangle trigonometry becomes powerful when we start looking at triangles in which we know an angle but don’t know all the sides.
Example \(\PageIndex{3}\)
Find the unknown sides of the triangle pictured here.
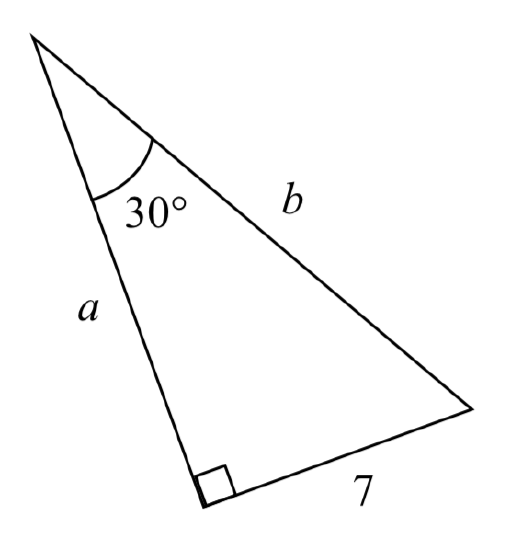
Solution
Since \(\text{sin} (\theta) = \dfrac{\text{opposite}}{\text{hypotenuse}}\). \(\text{sin}(30^{\circ}) = \dfrac{7}{b}\).
From this, we can solve for the side \(b\).
\[b\sin (30{}^\circ )=7\nonumber\]
\[b=\dfrac{7}{\sin (30{}^\circ )}\nonumber\]
To obtain a value, we can evaluate the sine and simplify
\[b = \dfrac{7}{1/2} = 14\nonumber\]
To find the value for side \(a\), we could use the cosine, or simply apply the Pythagorean Theorem:
\[a^2 + 7^2 = b^2\nonumber\]
\[a^2 + 7^2 = 14^2\nonumber\]
\[a = \sqrt{147}\nonumber\]
Notice that if we know at least one of the non-right angles of a right triangle and one side, we can find the rest of the sides and angles.
Exercise \(\PageIndex{2}\)
A right triangle has one angle of \(\dfrac{\pi }{3}\) and a hypotenuse of 20. Find the unknown sides and angles of the triangle.
- Answer
-
\[\text{cos} (\dfrac{\pi}{3}) = \dfrac{\text{adjacent}}{\text{hypoteuse}} = \dfrac{\text{Adj}}{20}\nonumber\] so, \[\text{adjacent} = 20 \text{cos} (\dfrac{\pi}{3}) = 20 (\dfrac{1}{2}) = 10\nonumber\]
\[\text{sin} (\dfrac{\pi}{3}) = \dfrac{\text{Opposite}}{\text{hypotenuse}} = \dfrac{\text{Opp}}{20}\nonumber\] so, \[\text{opposite} = 20 \text{sin} (\dfrac{\pi}{3}) = 20 (\dfrac{\sqrt{3}}{2}) = 10\sqrt{3}\nonumber\]
Missing angle = 180 - 90 - 60 = 30 degrees or \(\pi / 6\).
Example \(\PageIndex{4}\)
To find the height of a tree, a person walks to a point 30 feet from the base of the tree, and measures the angle from the ground to the top of the tree to be 57 degrees. Find the height of the tree.
Solution
We can introduce a variable, \(h\), to represent the height of the tree. The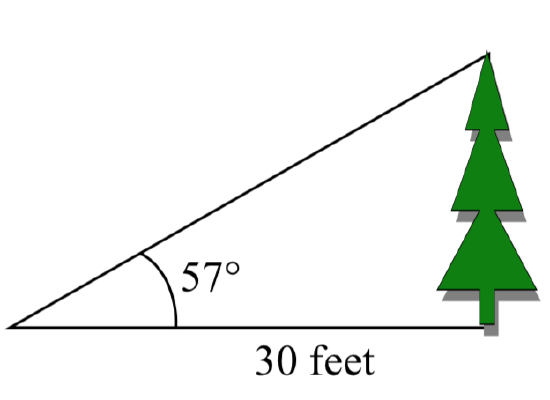 two sides of the triangle that are most important to us are the side opposite the angle, the height of the tree we are looking for, and the adjacent side, the side we are told is 30 feet long.
two sides of the triangle that are most important to us are the side opposite the angle, the height of the tree we are looking for, and the adjacent side, the side we are told is 30 feet long.
The trigonometric function which relates the side opposite of the angle and the side adjacent to the angle is the tangent.
\[\text{tan} (57^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{h}{30}\nonumber\] Solving for \(h\),
\[h=30\tan (57{}^\circ )\nonumber\] Using technology, we can approximate a value
\[h=30\tan (57{}^\circ )\approx 46.2\text{ feet}\nonumber\]
The tree is approximately 46 feet tall.
Example \(\PageIndex{5}\)
A person standing on the roof of a 100 foot tall building is looking towards a skyscraper a few blocks away, wondering how tall it is. She measures the angle of declination from the roof of the building to the base of the skyscraper to be 20 degrees and the angle of inclination to the top of the skyscraper to be 42 degrees.
Solution
To approach this problem, it would be good to start with a picture. Although we are interested in the height, 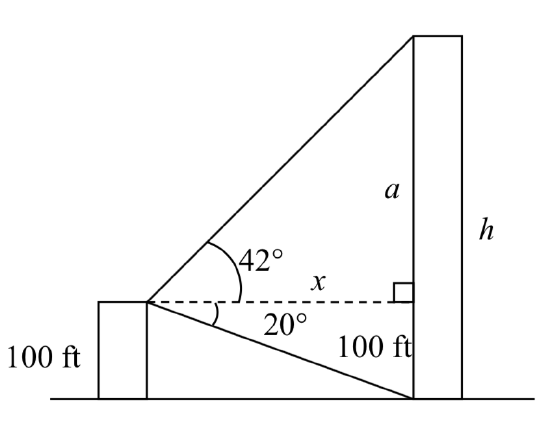 \(h\), of the skyscraper, it can be helpful to also label other unknown quantities in the picture – in this case the horizontal distance \(x\) between the buildings and \(a\), the height of the skyscraper above the person.
\(h\), of the skyscraper, it can be helpful to also label other unknown quantities in the picture – in this case the horizontal distance \(x\) between the buildings and \(a\), the height of the skyscraper above the person.
To start solving this problem, notice we have two right triangles. In the top triangle, we know one angle is 42 degrees, but we don’t know any of the sides of the triangle, so we don’t yet know enough to work with this triangle.
In the lower right triangle, we know one angle is 20 degrees, and we know the vertical height measurement of 100 ft. Since we know these two pieces of information, we can solve for the unknown distance \(x\).
\[\text{tan} (20^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{100}{x}\nonumber\] Solving for \(x\)
\[x \text{tan} (20^{\circ}) = 100\nonumber\]
\[x = \dfrac{100}{\text{tan} (20^{\circ})}\nonumber\]
Now that we have found the distance \(x\), we know enough information to solve the top right triangle.
\[\text{tan} (42^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{a}{x} = \dfrac{a}{100/\text{tan}(20^{circ})}\nonumber\]
\[\text{tan} (42^{\circ}) = \dfrac{a\text{tan} (20^{\circ})}{100}\nonumber\]
\[100 \text{tan} (42^{\circ}) = a\text{tan} (20^{\circ})\nonumber\]
\[\dfrac{\text{tan} (42^{\circ})}{\text{tan} (20^{\circ})} = a\nonumber\]
Approximating a value,
\[a=\dfrac{100\tan (42{}^\circ )}{\tan (20{}^\circ )} \approx 247.4\text{ feet}\nonumber\]
Adding the height of the first building, we determine that the skyscraper is about 347 feet tall.
Important Topics of This Section
- SOH CAH TOA
- Cofunction identities
- Applications with right triangles


