8.4: Vectors
- Page ID
- 13878
A woman leaves home, walks 3 miles north, then 2 miles southeast. How far is she from home, and in which direction would she need to walk to return home? How far has she walked by the time she gets home?
This question may seem familiar – indeed we did a similar problem with a boat in the first section of this chapter. In that section, we solved the problem using triangles. In this section, we will investigate another way to approach the problem using vectors, a geometric entity that indicates both a distance and a direction. We will begin our investigation using a purely geometric view of vectors.
A Geometric View of Vectors
Definition: VECTOR
A vector is an object that has both a length and a direction.
Geometrically, a vector can be represented by an arrow that has a fixed length and
indicates a direction. If, starting at the point \(A\), a vector, which means “carrier” in Latin, moves toward point \(B\), we write \(\overrightarrow{AB}\) to represent the vector.
A vector may also be indicated using a single letter in boldface type, like u, or by capping the letter representing the vector with an arrow, like \(\vec{u}\).
Example \(\PageIndex{1}\)
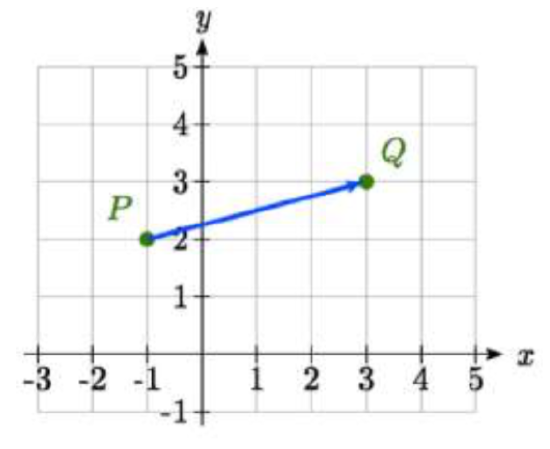
Draw a vector that represents the movement from the point \(P\) (-1, 2) to the point \(Q\) (3, 3)
Solution
By drawing an arrow from the first point to the second, we can construct a vector \(\overrightarrow {PQ}\).
Exercise \(\PageIndex{1}\)
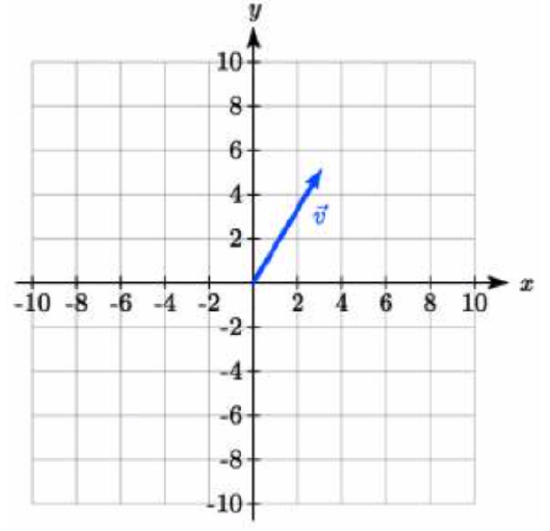
Draw a vector, \(\vec{v}\), that travels from the origin to the point (3, 5).
- Answer
-
Using this geometric representation of vectors, we can visualize the addition and scaling of vectors.
To add vectors, we envision a sum of two movements. To find \(\vec{u} + \vec{v}\), we first draw the vector \(\vec{u}\), then from the end of \(\vec{u}\) we drawn the vector \(\vec{v}\). This corresponds to the notion that first we move along the first vector, and then from that end position we move along the second vector. The sum \(\vec{u} + \vec{v}\) is the new vector that travels directly from the beginning of \(\vec{u}\) to the end of \(\vec{v}\) in a straight path.
ADDING VECTORS GEOMETRICALLY
To add vectors geometrically, draw \(\vec{v}\) starting from the end of \(\vec{u}\). The sum \(\vec{u} + \vec{v}\) is the vector from the beginn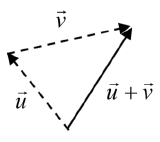 ing of \(\vec{u}\) to the end of \(\vec{v}\).
ing of \(\vec{u}\) to the end of \(\vec{v}\).
Example \(\PageIndex{2}\)
Given the two vectors shown below, draw \(\vec{u} + \vec{v}\)
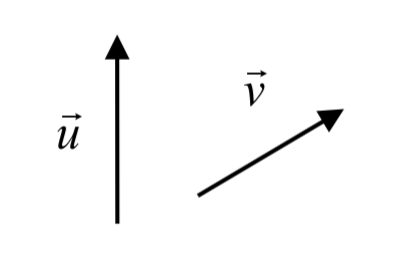
Solution
We draw \(\vec{v}\) starting from the end of \(\vec{u}\), then draw in the sum \(\vec{u} + \vec{v}\) from the beginning of \(\vec{u}\) to the end of \(\vec{v}\).
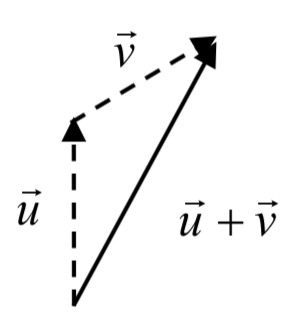
Notice that path of the walking woman from the beginning of the section could be visualized as the sum of two vectors. The resulting sum vector would indicate her end position relative to home.
Although vectors can exist anywhere in the plane, if we put the starting point at the origin it is easy to understand its size and direction relative to other vectors.
To scale vectors by a constant, such as \(3\vec{u}\), we can imagine adding \(\vec{u} + \vec{u} + \vec{u}\). The result will be a vector three times as long in the same direction as the original vector. If we were to scale a vector by a negative number, such as \(-\vec{u}\), we can envision this as the opposite of \(\vec{u}\); the vector so that \(\vec{u} + (-\vec{u}\) returns us to the starting point. This vector \(-\vec{u}\) would point in the opposite direction as \(\vec{u}\) but have the same length.
Another way to think about scaling a vector is to maintain its direction and multiply its length by a constant, so that \(3\vec{u}\) would point in the same direction but will be 3 times as long.
SCALING A VECTOR GEOMETRICALLY
To geometrically scale a vector by a constant, scale the length of the vector by the constant.
Scaling a vector by a negative constant will reverse the direction of the vector.
Example \(\PageIndex{3}\)
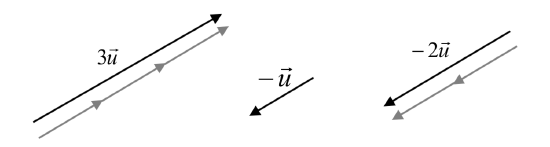
Given the vector shown, draw \(3\vec{u}\), \(-\vec{u}\), and \(-2\vec{u}\).
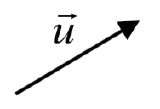
Solution
The vector \(3\vec{u}\) will be three times as long. The vector \(-\vec{u}\) will have the same length but point in the opposite direction. The vector \(-2\vec{u}\) will point in the opposite direction and be twice as long.
By combining scaling and addition, we can find the difference between vectors geometrically as well, since \(\vec{u} - \vec{v} = \vec{u} + (-\vec{v})\).
Example \(\PageIndex{4}\)
Given the vectors shown, draw \(\vec{u} - \vec{v}\)
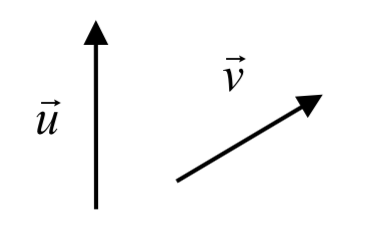
Solution
From the end of \(\vec{u}\) we draw \(-\vec{v}\), then draw in the result.
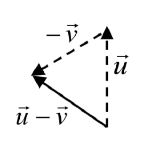
Notice that the sum and difference of two vectors are the two diagonals of a parallelogram with the vectors \(\vec{u}\) and \(\vec{v}\) as e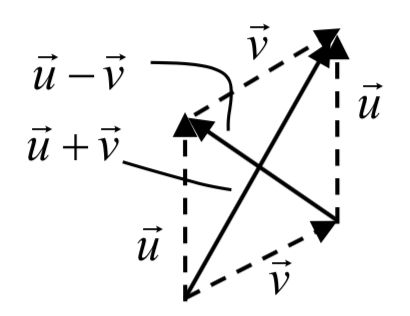 dges.
dges.
Exercise \(\PageIndex{2}\)
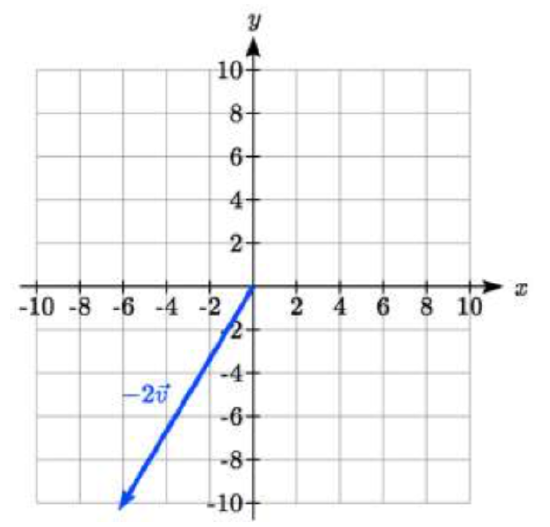
Using vector \(\vec{v}\) from previous Exercise, draw \(-2 \vec{v}\).
- Answer
-
Component Form of Vectors
While the geometric interpretation of vectors gives us an intuitive understanding of vectors, it does not provide us a convenient way to do ca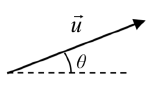 lculations. For that, we need a handy way to represent vectors. Since a vector involves a length and direction, it would be logical to want to represent a vector using a length and an angle \(\theta\), usually measured from standard position.
lculations. For that, we need a handy way to represent vectors. Since a vector involves a length and direction, it would be logical to want to represent a vector using a length and an angle \(\theta\), usually measured from standard position.
Definition: MAGNITUDE AND DIRECTION OF A VECTOR
A vector \(\vec{u}\) can be described by its magnitude, or length, \(|\vec{u}|\), and an angle \(\theta\).
A vector with length 1 is called unit vector.
While this is very reasonable, and a common way to describe vectors, it is often more convenient for calculations to represent a vector by horizontal and vertical components.
COMPONENT FORM OF A VECTOR
The component form of a vector represents the vector using two components. \(\vec{u} = \langle x, y \rangle\) indicates the vector represents a displacement of \(x\) units horizontally and \(y\) units vertically.
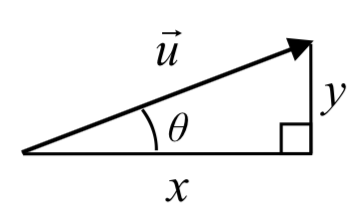
Notice how we can see the magnitude of the vector as the length of the hypotenuse of a right triangle, or in polar form as the radius, \(r\).
ALTERNATE NOTATION FOR VECTOR COMPONENTS
Sometimes you may see vectors written as the combination of unit vectors \(\vec{i}\) and \(\vec{j}\), where \(\vec{i}\) points the right and \(\vec{j}\) points up. In other words, \(\vec{i} = \langle 1, 0 \rangle\) and \(\vec{j} = \langle \theta, 1 \rangle\).
In this notation, the vector \(\vec{u} = \langle 3, -4 \rangle\) would be written as \(\vec{u} = 3\vec{i} - 4\vec{j}\) since both indicate a displacement of 3 units to the right, and 4 units down.
While it can be convenient to think of the vector \(\vec{u} = \langle x, y \rangle\) as an arrow from the origin to the point (\(x\), \(y\)), be sure to remember that most vectors can be situated anywhere in the plane, and simply indicate a displacement (change in position) rather than a position.
It is common to need to convert from a magnitude and angle to the component form of the vector and vice versa. Happily, this process is identical to converting from polar coordinates to Cartesian coordinates, or from the polar form of complex numbers to the \(a+bi\) form.
Example \(\PageIndex{5}\)
Find the component form of a vecor with length 7 at an angle of 135 degrees.
Solution
Using the conversion formulas \(x = r\cos(\theta)\) and \(y = r\sin(\theta)\), we can find the components
\[x = 7 \cos (135^{\circ}) = -\dfrac{7\sqrt{2}}{2}\nonumber\]
\[y = 7 \sin (135^{\circ}) = \dfrac{7\sqrt{2}}{2}\nonumber\]
The vector can be written in component form as \(\langle -\dfrac{7\sqrt{2}}{2}, \dfrac{7\sqrt{2}}{2} \rangle\)
Example \(\PageIndex{6}\)
Find the magnitude and angle \(\theta\) representing the vector \(\vec{u} = \langle 3, -2 \rangle\).
Solution
First we can find the magnitude by remembering the relationship between \(x\), \(y\) and \(r\):
\[r^2 = 3^2 + (-2)^2 = 13\nonumber\]
\[r = \sqrt{13}\nonumber\]
Second we can find the angle. Using the tangent,
\[\tan(\theta) = \dfrac{-2}{3}\nonumber\]
\[\theta = \tan^{-1}(-\dfrac{2}{3}) \approx -33.69^{\circ}\nonumber\]or written as a coterminal positive angle, \(326.31^{\circ}\). This angle is in the \(4^{\text{th}}\) quadrant as desired.
Exercise \(\PageIndex{3}\)
Using vector \(\vec{v}\) from the first Exercise, the vector that travels from the origin to the point (3, 5), find the components, magnitude and angle \(\theta\) that represent this vector.
- Answer
-
\[\vec{v} = \langle 3, 5 \rangle \nonumber\]
\[\text{magnitude} = \sqrt{34}\nonumber\]
\[\theta = \tan^{-1} (\dfrac{5}{3}) = 59.04^{\circ}\nonumber\]
In addition to representing distance movements, vectors are commonly used in physics and engineering to represent any quantity that has both direction and magnitude, including velocities and forces.
Example \(\PageIndex{7}\)
An object is launched with initial velocity 200 meters per second at an angle of 30 degrees. Find the initial horizontal and vertical velocities.
Solution
By viewing the initial velocity as a vector, we can resolve the vector into horizontal and vertical components.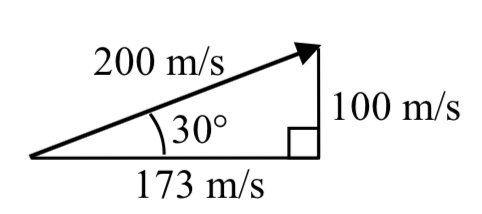
\[x = 200 \cos(30^{\circ} = 200 \cdot \dfrac{\sqrt{3}}{2} \approx 173.205\text{ m/sec}\nonumber\]
\[y = 200 \sin(30^{\circ} = 200 \cdot \dfrac{1}{2} = 100\text{ m/sec}\nonumber\]
This tells us that, absent wind resistance, the object will travel horizontally at about 173 meters each second. Gravity will cause the vertical velocity to change over time – we’ll leave a discussion of that to physics or calculus classes.
Adding and Scaling Vectors in Component Form
To add vectors in component form, we can simply add the corresponding components. To scale a vector by a constant, we scale each component by that constant.
COMBINING VECTORS IN COMPONENT FORM
To add, subtract, or scale vectors in component form
If \(\vec{u} = \langle u_1, u_2 \rangle\), \(\vec{v} = \langle v_1, v_2 \rangle\), and \(c\) is any constant, then
\[\vec{u} + \vec{v} = \langle u_1 + v_1, u_2 + v_2 \rangle\]
\[\vec{u} - \vec{v} = \langle u_1 - v_1, u_2 - v_2 \rangle\]
\[c\vec{u} = \langle cu_1, cu_2 \rangle\]
Example \(\PageIndex{8}\)
Given \(\vec{u} = \langle 3, -2 \rangle\) and \(\vec{v} = \langle -1, 4 \rangle\), find a new vector \(\vec{w} = 3\vec{u} - 2\vec{v}\)
Solution
Using the vectors given,
\[\begin{array} {rcl} {\vec{w}} &= & {3\vec{u} - 2\vec{v}} \\ {} &= & {3 \langle 3, -2 \rangle - 2\langle -1, 4 \rangle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Scale each vector}} \\ {} &= & {\langle 9, -6 \rangle - \langle -2, 8 \rangle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Subtract corresponding components}} \\ {} &= & {\langle 11, -14 \rangle} \end{array}\nonumber\]
By representing vectors in component form, we can find the resulting displacement vector after a multitude of movements without needing to draw a lot of complicated non- right triangles. For a simple example, we revisit the problem from the opening of the section. The general procedure we will follow is:
1) Convert vectors to component form
2) Add the components of the vectors
3) Convert back to length and direction if needed to suit the context of the question
Example \(\PageIndex{9}\)
A woman leaves home, walks 3 miles north, then 2 miles southeast. How far is she from home, and what direction would she need to walk to return home? How far has she walked by the time she gets home?
Solution
Let’s begin by understanding the question in a little more depth. When we use vectors to describe a traveling direction, we often position thin gs so north points in the upward direction, east points to the right, and so on, as pictured here.
gs so north points in the upward direction, east points to the right, and so on, as pictured here.
Consequently, travelling NW, SW, NE or SE, means we are travelling through the quadrant bordered by the given directions at a 45 degree angle.
With this in mind, we begin by converting each vector to components.
A walk 3 miles north would, in components, be \(\langle 0, 3 \rangle\).
A walk of 2 miles southeast would be at an angle of \(45^{\circ}\) South of East. Measuring from standard position the angle would be \(315^{\circ}\).
Converting to components, we choose to use the standard position angle so that we do not have to worry about whether the signs are negative or positive; they will work out automatically.
\[\langle 2\cos (315^{\circ}),\: 2\sin (315^{\circ })\rangle = \langle 2\cdot\frac{\sqrt{2}}{2},\:2\cdot\frac{-\sqrt{2}}{2}\rangle\approx\langle 1.414, -1.414\rangle\nonumber\]
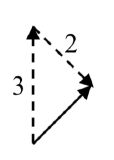
Adding these vectors gives the sum of the movements in component form
\[\langle 0, 3 \rangle + \langle 1.414, -1.414 \rangle = \langle 1.414 1.586 \rangle\nonumber\]
To find how far she is from home and the direction she would need to walk to return home, we could find the magnitude and angle of this vector.
\[\text{Length} = \sqrt{1.414^2 + 1.586^2} = 2.125\nonumber\]
To find the angle, we can use the tangent
\[\tan(\theta) = \dfrac{1.586}{1.414}\nonumber\]
\[\theta = tan^{-1} (\dfrac{1.586}{1.414}) = 48.273^{\circ}\text{ north of east}\nonumber\]
Of course, this is the angle from her starting point to her ending point. To return home, she would need to head the opposite direction, which we could either describe as \(180^{\circ} + 48.273^{\circ} = 228.273^{\circ}\) measured in standard position, or as \(48.273^{\circ}\) south of west (or \(41.727^{\circ}\) west of south).
She has walked a total distance of 3 + 2 + 2.125 = 7.125 miles.
Keep in mind that total distance traveled is not the same as the length of the resulting displacement vector or the “return” vector.
Exercise \(\PageIndex{4}\)
In a scavenger hunt, directions are given to find a buried treasure. From a starting point at a flag pole you must walk 30 feet east, turn 30 degrees to the north and travel 50 feet, and then turn due south and travel 75 feet. Sketch a picture of these vectors, find their components, and calculate how far and in what direction you must travel to go directly to the treasure from the flag pole without following the map.
- Answer
-
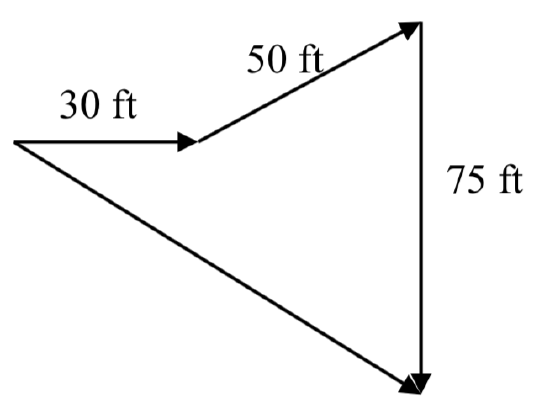
\[\vec{v}_1 = \langle 30, 0 \rangle\quad \vec{v}_2 = \langle 50\cos(30^{\circ}), 50\sin(30^{circ}) \rangle\quad \vec{v}_3 = \langle 0, -75 \rangle\nonumber\]
\[\vec{v}_f = \langle 30 + 50 \cos(30^{\circ}), 50 \sin(30^{\circ}) - 75 \rangle = \langle 73.301, -50 \rangle\nonumber\]
Magnitude = 88.73 feet at an angle of \(34.3^{\circ}\) south of east.
While using vectors is not much faster than using law of cosines with only two movements, when combining three or more movements, forces, or other vector quantities, using vectors quickly becomes much more efficient than trying to use triangles.
Example \(\PageIndex{10}\)
Three forces are acting on an object as shown below, each measured in Newtons (N). What force must be exerted to keep the object in equilibrium (where the sum of the forces is zero)?
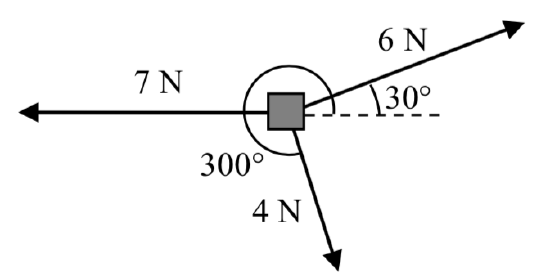
Solution
We start by resolving each vector into components.
The first vector with magnitude 6 Newtons at an angle of 30 degrees will have components
\[\langle 6\cos(30^{\circ}). 6\sin(30^{\circ}) \rangle = \langle 6 \cdot \dfrac{\sqrt{3}}{2}, 6 \cdot \dfrac{1}{2} \rangle = \langle 3\sqrt{3} 3 \rangle\nonumber\]
The second vector is only in the horizontal direction, so can be written as \(\langle -7, 0 \rangle\).
The third vector with magnitude 4 Newtons at an angle of 300 degrees will have components
\[\langle 4 \cos(300^{\circ}), 4\sin(300^{\circ}) \rangle = \langle 4 \cdot \dfrac{1}{2}, 4 \cdot \dfrac{-\sqrt{3}}{2} \rangle = \langle 2, -2\sqrt{3} \rangle\nonumber\]
To keep the object in equilibrium, we need to find a force vector \(x\), \(y\) so the sum of the four vectors is the zero vector, \(\langle 0, 0 \rangle\).
\[\langle 3\sqrt{3}, 3 \rangle + \langle -7, 0 \rangle + \langle 2, -2\sqrt{3} \rangle + \langle x, y \rangle = \langle 0, 0 \rangle\nonumber\]Add component-wise
\[\langle 3\sqrt{3} - 7 + 2, 3 + 0 - 2\sqrt{3} \rangle + \langle x, y \rangle = \langle 0, 0 \rangle\nonumber\]Simplify
\[\langle 3\sqrt{3} - 5, 3 - 2\sqrt{3} \rangle + \langle x, y \rangle = \langle 0, 0 \rangle\nonumber\]Solve
\[\langle x, y \rangle = \langle 0, 0 \rangle - \langle 3\sqrt{3} - 5, 3 - 2\sqrt{3} \rangle\nonumber\]
\[\langle x, y \rangle = \langle -3\sqrt{3} + 5, -3 + 2\sqrt{3} \rangle \approx \langle -0.196, 0.464 \rangle\nonumber\]
This vector gives in components the force that would need to be applied to keep the object in equilibrium. If desired, we could find the magnitude of this force and direction it would need to be applied in.
\[\text{Magnitude} = \sqrt{(-0.196)^2 + 0.464^2} = 0.504\text{ N}\nonumber\]
Angle:
\[\tan(\theta) = \dfrac{0.464}{-0.196}\nonumber\]
\[\theta = \tan^{-1} (\dfrac{0.464}{-0.196} = -67.089^{\circ}\nonumber\]
This is in the wrong quadrant, so we adjust by finding the next angle with the same tangent value by adding a full period of tangent:
\[\theta = -67.089^{\circ} + 180^{\circ} = 112. 911^{circ}\nonumber\]
To keep the object in equilibrium, a force of 0.504 Newtons would need to be applied at an angle of \(112.911^{\circ}\)
Important Topics of This Section
- Vectors, magnitude (length) & direction Addition of vectors
- Scaling of vectors
- Components of vectors
- Vectors as velocity
- Vectors as forces
- Adding & Scaling vectors in component form Total distance travelled vs. total displacement


