1.2: The Cosine and Sine Functions
- Page ID
- 7098
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- If the real number \(t\) represents the (signed) length of an arc, how do we define \(\cos(t)\) and \(\sin(t)\)?
- In what quadrants (of the terminal point of an arc t on the unit circle) is \(\cos(t)\) positive (negative)? In what quadrants (of the terminal point of an arc \(t\) on the unit circle) is \(\sin(t)\) positive (negative)?
- What is the Pythagorean Identity? How is this identity derived from the equation for the unit circle?
Beginning Activity
- What is the unit circle? What is the equation of the unit circle?
- Review Exercise 1.4 on page 9.
- Review the completed version of Figure1.4 that is in the answers for Exercise 1.2 on page 6.
- What is the terminal point of the arc on the unit circle that corresponds to the interval \([0, \dfrac{\pi}{2}]\)?
- What is the terminal point of the arc on the unit circle that corresponds to the interval \([0, \pi]\)?
- What is the terminal point of the arc on the unit circle that corresponds to the interval \([0, \dfrac{3\pi}{2}]\)?
- What is the terminal point of the arc on the unit circle that corresponds to the interval \([0, -\dfrac{\pi}{2}]\)?
The Cosine and Sine Functions
We started our study of trigonometry by learning about the unit circle, how to wrap the number line around the unit circle, and how to construct arcs on the unit circle. We are now able to use these ideas to define the two major circular, or trigonometric, functions. These circular functions will allow us to model periodic phenomena such as tides, the amount of sunlight during the days of the year, orbits of planets, and many others.
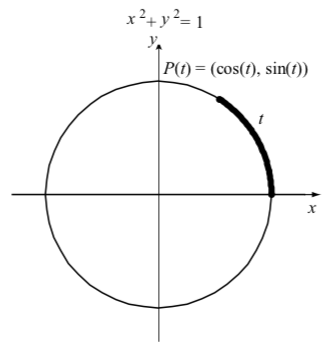
Figure \(\PageIndex{1}\): The Circular Functions
It may seem like the unit circle is a fairly simple object and of little interest, but mathematicians can almost always find something fascinating in even such simple objects. For example, we define the two major circular functions, the cosine and sine in terms of the unit circle as follows. Figure \(\PageIndex{1}\) shows an arc of length \(t\) on the unit circle. This arc begins at the point \((1, 0)\) and ends at its terminal point \(P(t)\). We then define the cosine and sine of the arc \(t\) as the \(x\) and \(y\) coordinates of the point \(P\), so that \(P(t) = (\cos(t), sin(t))\) (we abbreviate the cosine as \(\cos\) and the sine as \(\sin\)). So the cosine and sine values are determined by the arc \(t\) and the cosine and sine are functions of the arc \(t\). Since the arc lies on the unit circle, we call the cosine and sine circular functions. An important part of trigonometry is the study of the cosine and sine and the periodic phenomena that these functions can model. This is one reason why the circular functions are also called the trigonometric functions.
Note
According to the web site Earliest Known Uses of Some of the Words of Mathematics at jeff560.tripod.com/mathword.html, the origin of the word sine is Sanskrit through Arabic and Latin. While the accounts of the actual origin differ, it appears that the Sanskrit work “jya” (chord) was taken into Arabic as “jiba”, but was then translated into Latin as “jaib” (bay) which became “sinus” (bay or curve). This word was then anglicized to become our “sine”. The word cosine began with Plato of Tivoli who use the expression “chorda residui”. While the Latin word chorda was a better translation of the Sanskrit-Arabic word for sine than the word sinus, that word was already in use. Thus, “chorda residui” became “cosine”.
Note
In mathematics, we always create formal definitions for objects we commonly use. Definitions are critically important because with agreed upon definitions, everyone will have a common understanding of what the terms mean. With- out such a common understanding, there would be a great deal of confusion since different people who have different meanings for various terms. So careful and precise definitions are necessary in order to develop mathematical properties of these objects. In order to learn and understand trigonometry, a person needs to be able to explain how the circular functions are defined. So now is a good time to start working on understanding these definitions.
Definitions: cosine & Sine
If the real number t is the directed length of an arc (either positive or negative) measured on the unit circle \(x^2 + y^2 = 1\) (with counterclockwise as the positive direction) with initial point \((1, 0)\) and terminal point \((x, y)\), then the cosine of \(t\), denoted \(\cos(t)\), and sine of t, denoted \(\sin(t)\), are defined to be \[\cos (t) = x\] and \[\sin (t) = y.\]
Figure 1.6 illustrates these definitions for an arc whose terminal point is in the first quadrant.
At this time, it is not possible to determine the exact values of the cosine and sine functions for specific values of \(t\). It can be done, however, if the terminal point of an arc of length \(t\) lies on the \(x\)-axis or the \(y\)-axis. For example, since the circumference of the unit circle is \(2\pi\), an arc of length \(t = \pi\) will have it terminal point half-way around the circle from the point \((1, 0)\). That is, the terminal point is at \((1, 0)\). Therefore, \[\cos (\pi) = -1\] and \[\sin (\pi) = 0.\]
Exercise \(\PageIndex{1}\)
Determine the exact values of each of the following:
- \(\cos(\dfrac{\pi}{2})\) and \(\sin(\dfrac{\pi}{2})\).
- \(\cos(\dfrac{3\pi}{2})\) and \(\sin(\dfrac{3\pi}{2})\).
- \(\cos(0)\) and \(sin(0)\).
- \(\cos(-\dfrac{\pi}{2})\) and \(\sin(-\dfrac{\pi}{2})\).
- \(\cos(2\pi)\) and \(\sin(2\pi)\).
- \(cos(-\pi)\) and \(\sin(-\pi)\).
Important Note: Since the cosine and sine are functions of an arc whose length is the real number t, the input t determines the output of the cosine and sin. As a result, it is necessary to specify the input value when working with the cosine and sine. In other words, we ALWAYS write \(\cos(t)\) where \(t\) is the real number input, and NEVER just \(\cos\). To reiterate, the cosine and sine are functions, so we MUST indicate the input to these functions.
- Answer
-
- \[\cos(\dfrac{\pi}{2}) = 0\] \[\sin(\dfrac{\pi}{2}) = 1\]
- \[\cos(\dfrac{3\pi}{2}) = 0\] \[\sin(\dfrac{3\pi}{2}) = -1\]
- \[\cos(0) = 1\] \[\sin(0) = 1\]
- \[\cos(-\dfrac{\pi}{2}) = 0\] \[\sin(-\dfrac{\pi}{2}) = -1\]
- \[\cos(2\pi) = 0\] \[\sin(2\pi) = 1\]
- \[\cos(-\pi) = -1\] \[\sin(-\pi) = 0\]
Exercise \(\PageIndex{2}\)
For this Exercise, we will use the Geogebra Applet called Terminal Points of Arcs on the Unit Circle. A web address for this applet is
For this applet, we control the value of the input \(t\) with the slider for \(t\). The values of \(t\) range from \(-20\) to \(20\) in increments of \(0.5\). For a given value of \(t\), an arc is drawn of length \(t\) and the coordinates of the terminal point of that arc are displayed. Use this applet to find approximate values for each of the following:
- \(\cos(1)\) and \(\sin(1)\)
- \(\cos(2)\) and \(\sin(2)\)
- \(\cos(-4)\) and \(\sin(-4)\)
- \(\cos(5.5)\) and \(\sin(5.5)\)
- \(\cos(15)\) and \(\sin(15)\)
- \(\cos(-15)\) and \(\sin(-15)\)
- Answer
-
- \[\cos(1) \approx 0.5403, \sin(1) \approx 0.8415\]
- \[\cos(2) \approx -0.4161, \sin(2) \approx 0.9093\]
- \[\cos(-4) \approx -0.6536, \sin(-4) \approx 0.7568\]
- \[\cos(5.5) \approx 0.7807, \sin(5.5) \approx -0.7055\]
- \[\cos(15) \approx -0.7597, \sin(15) \approx 0.6503\]
- \[\cos(-15) \approx -0.7597, \sin(-15) \approx 0.6503\]
Some Properties of the Cosine and Sine Functions
The cosine and sine functions are called circular functions because their values are determined by the coordinates of points on the unit circle. For each real number \(t\), there is a corresponding arc starting at the point \((1, 0)\) of (directed) length \(t\) that lies on the unit circle. The coordinates of the end point of this arc determines the values of \(\cos(t\) and \(\sin(t\).
In previous mathematics courses, we have learned that the domain of a function is the set of all inputs that give a defined output. We have also learned that the range of a function is the set of all possible outputs of the function.
Exercise \(\PageIndex{3}\)
- What is the domain of the cosine function? Why?
- What is the domain of the sine function? Why?
- What is the largest \(x\) coordinate that a point on the unit circle can have? What is the smallest \(x\) coordinate that a point on the unit circle can have? What does this tell us about the range of the cosine function? Why?
- What is the largest \(y\) coordinate that a point on the unit circle can have? What is the smallest \(y\) coordinate that a point on the unit circle can have? What does this tell us about the range of the sine function? Why?
- Answer
-
- Since we can wrap any number onto the unit circle, we can always find the terminal point of an arc that corresponds to any number. So the cosine of any real number is defined and the domain of the cosine function is the set of all of the real numbers.
- For the same reason as for the cosine function, the domain of the sine function is the set of all real numbers.
- On the unit circle, the largest x-coordinate a point can have is 1 and the smallest x-coordinate a point can have is 1. Since the output of the cosine function is the x-coordinate of a point on the unit circle, the range of the cosine function is the closed interval \([-1, 1]\). That means \(-1 \leq \cos(t) \leq 1\) for any real number \(t\).
- On the unit circle, the largest y-coordinate a point can have is 1 and the smallest y-coordinate a point can have is 1. Since the output of the sine function is the y-coordinate of a point on the unit circle, the range of the sine function is the closed interval \([-1, 1]\). That means \(-1 \leq \sin(t) \leq 1\) for any real number \(t\).
Although we may not be able to calculate the exact values for many inputs for the cosine and sine functions, we can use our knowledge of the coordinate system and its quadrants to determine if certain values of cosine and sine are positive or negative. The idea is that the signs of the coordinates of a point \(P(x, y)\) that is plotted in the coordinate plan are determined by the quadrant in which the point lies (unless it lies on one of the axes). Figure \(\PageIndex{2}\) summarizes these results for the signs of the cosine and sine function values. The left column in the table is for the location of the terminal point of an arc determined by the real number \(t\).
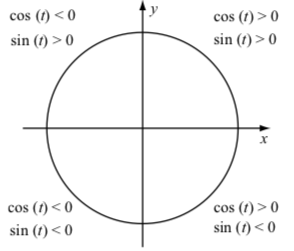
| Quadrant | \(\cos(t)\) | \(\sin(t)\) |
|---|---|---|
| QI | positive | positive |
| QII | negative | positive |
| QIII | negative | negative |
| QIV | positive | negative |
What we need to do now is to determine in which quadrant the terminal point of an arc determined by a real number t lies. We can do this by once again using the fact that the circumference of the unit circle is \(2\pi\), and when we move around the unit circle from the point .1; 0/ in the positive (counterclockwise) direction, we will intersect one of the coordinate axes every quarter revolution. For example, if \(0 < t < \dfrac{\pi}{2}\), the terminal point of the arc determined by \(t\) is in the first quadrant and \(\cos(t) > 0\) and \(\sin(t) > 0\).
Exercise \(\PageIndex{4}\)
- If \( \dfrac{\pi}{2} < t < \pi\), then what are the signs of \(\cos(t)\) and \(\sin(t)\)?
- If \( \pi < t < \dfrac{3\pi}{2}\), then what are the signs of \(\cos(t)\) and \(\sin(t)\)?
- If \( \dfrac{3\pi}{2} < t < 2\pi\), then what are the signs of \(\cos(t)\) and \(\sin(t)\)?
- If \( \dfrac{5\pi}{2} < t < 3\pi\), then what are the signs of \(\cos(t)\) and \(\sin(t)\)?
- For which values of \(t\) (between \(0\) and \(2\pi\)) is \(\cos(t)\) positive? Why?
- For which values of \(t\) (between \(0\) and \(2\pi\)) is \(\sin(t)\) positive? Why?
- For which values of \(t\) (between \(0\) and \(2\pi\)) is \(\cos(t)\) negative? Why?
- For which values of \(t\) (between \(0\) and \(2\pi\)) is \(\sin(t)\) negative? Why?
- Answer
-
- If \(\dfrac{\pi}{2} < t < \pi\), then the terminal point of the arc \(t\) is in the second quadrant and so \(\cos(t) < 0\) and \(\sin(t) > 0\).
- If \(\pi < t < \dfrac{3\pi}{2}\), then the terminal point of the arc t is in the third quadrant and so \(\cos(t) < 0\) and \(\sin(t) < 0\).
- If \(\dfrac{3\pi}{2} < t < 2\pi\), then the terminal point of the arc t is in the fourth quadrant and so \(\cos(t) > 0\) and \(\sin(t) < 0\).
- If \(\dfrac{5\pi}{2} < t < 3\pi\), then the terminal point of the arc t is in the second quadrant and so \(\cos(t) > 0\) and \(\sin(t) > 0\).
- Note that \(\cos(t) = 0\) at \(t = \dfrac{\pi}{2}\) and \(t = \dfrac{3\pi}{2}\). Since \(\cos(t)\) is the x-coordinate of the terminal point of the arc \(t\), the previous response shows that \(\cos(t)\) is positive when \(t\) is in one of the intervals \([0, \dfrac{\pi}{2})\) or \((\dfrac{3\pi}{2}, 2\pi]\).
- Note that \(\sin(t) = 0\) at \(t = 0\) and \(t = \pi\). Since \(\sin(t)\) is the x-coordinate of the terminal point of the arc \(t\), the previous response shows that \(\sin(t)\) is positive when \(t\) is in one of the intervals \((0, \pi)\).
- Note that \(\cos(t) = 0\) at \(t = \dfrac{\pi}{2}\) and \(t = \dfrac{3\pi}{2}\). Since \(\cos(t)\) is the x-coordinate of the terminal point of the arc \(t\), the previous response shows that \(\cos(t)\) is positive when \(t\) is in the interval \((\dfrac{\pi}{2}, \dfrac{3\pi}{2})\).
- Note that \(\sin(t) = 0\) at \(t = \pi\) and \(t = 2\pi\). Since \(\sin(t)\) is the x-coordinate of the terminal point of the arc \(t\), the previous response shows that \(\sin(t)\) is positive when \(t\) is in one of the intervals \([0, \dfrac{\pi}{2})\) or \((\pi, 2\pi)\).
Exercise \(\PageIndex{5}\)
Use the results summarized in Figure \(\PageIndex{2}\) to help determine if the following quantities are positive, negative, or zero. (Do not use a calculator.)
- \(\cos(\dfrac{\pi}{5})\)
- \(\sin(\dfrac{\pi}{5})\)
- \(\cos(\dfrac{5\pi}{8})\)
- \(\sin(\dfrac{5\pi}{8})\)
- \(\cos(\dfrac{-9\pi}{16})\)
- \(\sin(\dfrac{-9\pi}{16})\)
- \(\cos(\dfrac{-25\pi}{12})\)
- \(\sin(\dfrac{-25\pi}{12})\)
- Answer
-
- Since \(0 < \dfrac{\pi}{5} < \dfrac{\pi}{2}\), the terminal point of the arc \(\dfrac{\pi}{5}\) is in the first quadrant. Therefore, \(\cos(\dfrac{\pi}{5})\) is positive.
- Using the information about \(t\) in (1), \(\sin(\dfrac{\pi}{5})\) is positive.
- We can write \(\dfrac{\pi}{2}\) as \(\dfrac{4\pi}{8}\) and \(\pi\) as \(\dfrac{8\pi}{8}\), so \(\dfrac{\pi}{2}\ < \dfrac{5\pi}{8} < \pi\). This puts the terminal point of the arc \(\dfrac{5\pi}{8}\) in the second quadrant. Therefore, \(\cos(\dfrac{5\pi}{8})\) is negative.
- Using the information about \(t\) in (3), \(\sin(\dfrac{5\pi}{8})\) is negative.
- We can write \(-\dfrac{\pi}{2}\) as \(\dfrac{-8\pi}{16}\) and \(-\pi\) as \(\dfrac{-16\pi}{16}\), so \(-\pi < \dfrac{-9\pi}{16} < -\dfrac{\pi}{2}\). This puts the terminal point of the arc \(\dfrac{-9\pi}{16}\) in the third quadrant. Therefore, (\cos(\dfrac{-9\pi}{16})\) is negative.
- Using the information about \(t\) in (5), (\sin(\dfrac{-9\pi}{16})\) is negative.
- We can write \(-2\pi\) as \(\dfrac{-24\pi}{12}\) and \(-\dfrac{5\pi}{2}\) as \(\dfrac{-30\pi}{12}\), so \(\dfrac{-5\pi}{2} < \dfrac{-25\pi}{12} < 2\pi\). This puts the terminal point of the arc \(\cos(\dfrac{-25\pi}{12})\) in the fourth quadrant.
- Using the information about the arc \(t\) in (7), \(\sin(\dfrac{-25\pi}{12})\) is negative.
The Pythagorean Identity
In mathematics, an identity is a statement that is true for all values of the variables for which it is defined. In previous courses, we have worked with algebraic identities such as
\[7x+12x = 19x\] \[a^2 - b^2 = (a + b)(a - b)\]
\[a + b = b + a\]
\[x(y + z) = xy + xz\]
where it is understood that all the variables represent real numbers. In trigonometry, we will develop many so-called trigonometric identities. The following Exercise introduces one such identity between the cosine and sine functions.
Exercise \(\PageIndex{6}\)
We know that the equation for the unit circle is \(x^2 + y^2 = 1\). We also know that if \(t\) is an real number, then the terminal point of the arc determined by \(t\) is the point \((\cos(t), \sin(t))\) and that this point lies on the unit circle. Use this information to develop an identity involving \(\cos(t)\) and \(\sin(t)\).
- Answer
-
Any point on the unit circle satisfies the equation \(x^{2} + y^{2} = 1\). Since \((\cos(t), \sin(t))\) is a point on the unit circle, it follows that \((\cos(t))^{2} + (\sin(t))^{2} = 1\) or \[\cos^{2}(t) + \sin^{2}(t) = 1.\]
Definition: Pythagorean Identity
Using the definitions \(x = \cos(t)\) and \(y = \sin(t)\) along with the equation for the unit circle, we obtain the following identity, which is perhaps the most important trigonometric identity.
For each real number \(t\),
\[(\cos(t))^2 + (\sin(t))^2 = 1.\]
This is called the Pythagorean Identity. We often use the shorthand notation \(\cos^2(t)\) for \((\cos(t))^2\) and \(\sin^2(t)\) for \((\sin(t))^2\) and write
\[\cos^2(t) + \sin^2(t) = 1.\]
Important Note about Notation:
Always remember that by \(\cos^2(t)\) we mean \((\cos(t))^2\). In addition, note that \(\cos^2(t)\) is different from \(\cos(t^2)\).
The Pythagorean Identity allows us to determine the value of \(\cos(t)\) or \(\sin(t)\) if we know the value of the other one and the quadrant in which the terminal point of arc \(t\) lies. This is illustrated in the next example.
Example \(\PageIndex{1}\)
Assume that \(\cos(t) = \dfrac{2}{5}\) and the terminal point of arc\((t)\) lies in the fourth quadrant.5 Use this information to determine the value of \(\sin(t)\).
Solution
The primary tool we will use is the Pythagorean Identity, but please keep in mind that the terminal point for the arc \(t\) is the point \((\cos(t), \sin(t))\). That is, \(x = \cos(t)\) and \(y = \sin(t)\) So this problem is very similar to using the equation \(x^2 + y^2 = 1\) for the unit circle and substituting \(x = \dfrac{2}{5}\).
Using the Pythagorean Identity, we then see that
\[\cos^2(t) + \sin^2(t) = 1\]
\[ (\dfrac{2}{5})^2+ \sin^2(t) = 1\]
\[\dfrac{4}{25} + \sin^2(t) = 1\]
\[ \sin^2(t) = 1 - \dfrac{4}{25} \]
\[ \sin^2(t) = \dfrac{21}{25} \]
This means that \(\sin(t) = \pm\sqrt{\dfrac{21}{25}}\), and since the terminal point of arc\((t)\) is in the fourth quadrant, we know that \(\sin(t) < 0\). Therefore, \(\sin(t) = -\sqrt{\dfrac{21}{25}}\). Since \(\sqrt{25} = 5\), we can write
\[\sin(t) = -\sqrt{\dfrac{21}{25}} = -\dfrac{\sqrt{21}}{5}.\]
Exercise \(\PageIndex{7}\)
- If \(\cos(t) = \dfrac{1}{2}\) and the terminal point of the arc \(t\) is in the fourth quadrant, determine the value of \(\sin(t)\).
- If \(\sin(t) = -\dfrac{2}{3}\) and \(\pi < t < \dfrac{3\pi}{2}\), determine the value of \(\cos(t)\).
- Answer
-
1. Since \(\cos(t) = \dfrac{1}{2}\), we can use the Pythagorean Identity to obtain
\[(\dfrac{1}{2})^{2} + \sin^{2}(t) = 1]
\[\dfrac{1}{4} + \sin^{2}(t) = 1\]
\[\sin^{2}(t) = \dfrac{3}{4}\]
\[\sin(t) = \pm\dfrac{\sqrt{3}}{4}\]
Notice that we cannot determine the sign of \(\sin(t)\) using only the Pythagorean Identity. We need further information about the arc \(t\). In this case, we are given that the terminal point of the arc \(t\) is in the fourth quadrant, and hence, \(\sin(t) < 0\). Consequently,
\[\sin(t) = -\sqrt{\dfrac{3}{4}} = -\dfrac{\sqrt{3}}{2}\]
2. Since \(\sin(t) = -\dfrac{2}{3}\), we can use the Pythagorean Identity to obtain
\[\cos^{2}(t) + (-\dfrac{2}{3})^{2} = 1]
\[\cos^{2}(t) + \dfrac{4}{9} = 1\]
\[\cos^{2}(t) = \dfrac{5}{9}\]
\[\sin(t) = \pm\dfrac{\sqrt{5}}{9}\]
Once again, we need information about the arc \(t\) to determine the sign of \(\cos(t)\). In this case, we are given that \(\pi < t < \dfrac{3\pi}{2}\). Hence, the terminal point of the arc t is in the third quadrant and so, \(\sin(t) < 0\). Therefore,
\[\cos(t) = -\sqrt{\dfrac{5}{9}} = \dfrac{\sqrt{5}}{3}.\]
Summary
In this section, we studied the following important concepts and ideas:
- If the real number t is the directed length of an arc (either positive or negative) measured on the unit circle \(x^2 + y^2 = 1\) (with counterclockwise as the positive direction) with initial point \((1, 0)\) and terminal point \((x, y)\), then \(\cos(t) = x\) and \(\sin(t) = y\).

- The signs of \(\cos(t)\) and \(\sin(t)\) are determined by the quadrant in which the terminal point of an arc \(t\) lies.
| Quadrant | \(\cos(t)\) | \(\sin(t)\) |
|---|---|---|
| QI | positive | positive |
| QII | negative | positive |
| QIII | negative | negative |
| QIV | positive | negative |
- One of the most important identities in trigonometry, called the Pythagorean Identity, is derived from the equation for the unit circle and states:
For each real number \(t\), \[\cos^2(t) + \sin^2(t) = 1.\nonumber\]


