2.E: Graphs of the Trigonometric Functions (Exercises)
- Page ID
- 17333
Exercise \(\PageIndex{1}\)
In each of the following, the graph on the left shows the terminal point of an arc \(t\) (with \(0 \leq t \leq 2\pi\)) on the unit circle. The graphs on the right show the graphs of \(y = \cos(t)\) and \(y = \sin(t)\) with some points on the graph labeled. Match the point on the graphs of \(y = \cos(t)\) and \(y = \sin(t)\) that correspond to the point on the unit circle. In addition, state the coordinates of the points on \(y = \cos(t)\) and \(y = \sin(t)\).
(a)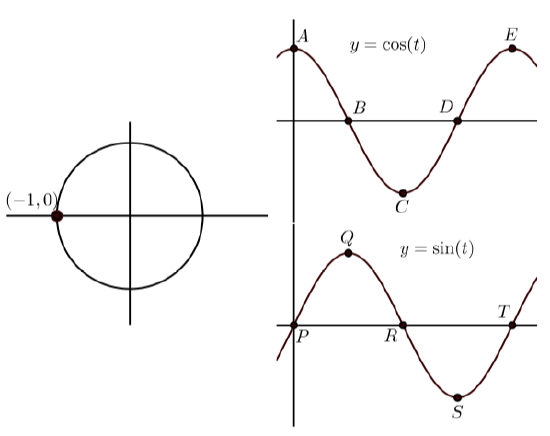
(b)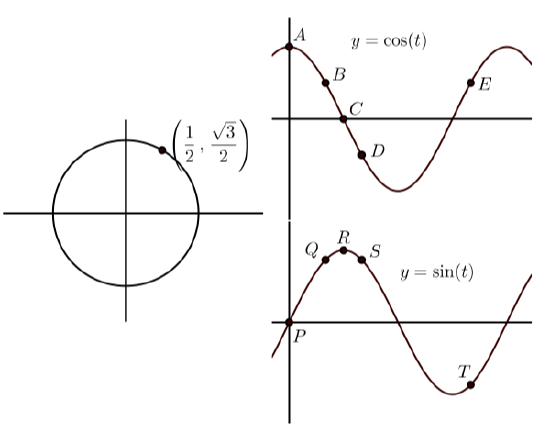
(c)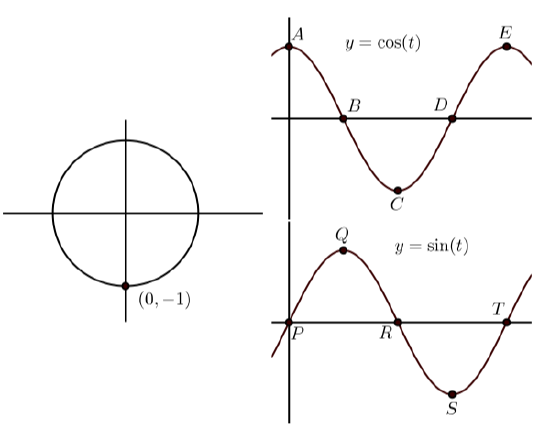
(d)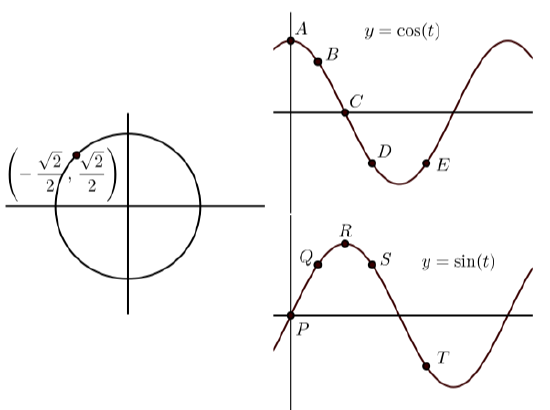
- Answer
-
(a) \(C(\pi, -1)\) \(R(\pi, 0)\)
(b) \(B(\dfrac{\pi}{3}, \dfrac{1}{2})\) \(Q(\dfrac{\pi}{3}, \dfrac{\sqrt{3}}{2})\)
Exercise \(\PageIndex{2}\)
For each of the following, determine an equation of the form \(y = A\cos(t)\) or \(y = A\sin(t)\)for the given graph.
-
(a)
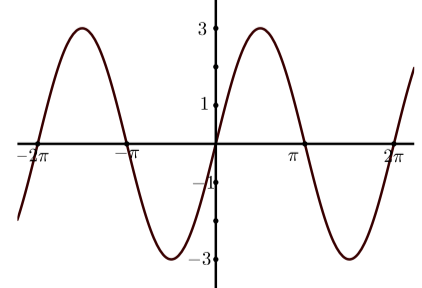
(b)
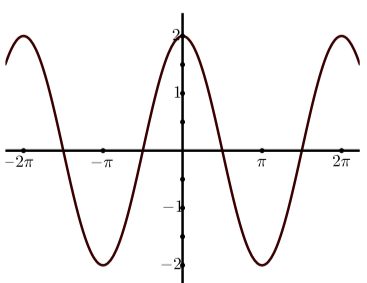
(c)
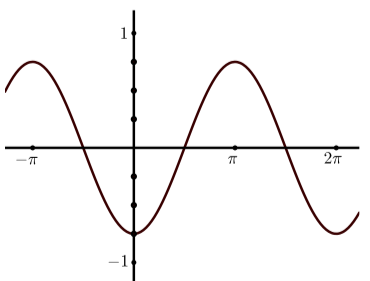
- Answer
-
(a) \(y = 3\sin(x)\)
(b) \(y = 2\cos(x)\)
Exercise \(\PageIndex{3}\)
Draw the graph of each of the following sinusoidal functions over the indicated interval. For each graph,
- State the \(t\)-intercepts on the given interval.
- State the \(y\)-intercept.
- State the maximum value of the function and the coordinates of all the points where the maximum value occurs.
- State the minimum value of the function and the coordinates of all the points where the minimum value occurs.
- \(y = \sin(t)\) with \(-2\pi \leq t \leq 2\pi\).
- \(y = 3\cos(t)\) with \(-\pi \leq t \leq 3\pi\).
- \(y = 5\sin(t)\) with \(0 \leq t\leq 4\pi\).
- \(y = \dfrac{3}{7}\cos(t)\) with \(-\pi \leq t \leq 3\pi\).
- \(y = -2.35\sin(t)\) with \(-\pi \leq t \leq \pi\).
- \(y = -4\cos(t)\) with \(0 \leq t \leq 6\pi\).
- Answer
-
(a) \(t\)-intercepts: \(-2\pi, -\pi, 0, \pi, 2\pi\), \(y\)-intercept: \((0, 0)\)
The maximum value is \(1\). Maximum value occurs at the points \((-\dfrac{3\pi}{2}, 1)\) and \((\dfrac{\pi}{2}, 1)\).
The minimum value is \(-1\). Minimum value occurs at the points \((-\dfrac{\pi}{2}, -1)\) and \((\dfrac{3\pi}{2}, -1)\).
(b) \(t\)-intercepts: \(-\dfrac{3\pi}{2}, -\dfrac{\pi}{2}, \dfrac{\pi}{2}, \dfrac{3\pi}{2}\), \(y\)-intercept: \((0, 2)\)
The maximum value is \(2\). Maximum value occurs at the points \((0, 2)\) and \((2\pi, 2)\).
The minimum value is \(-2\). Minimum value occurs at the points \((-\pi -2)\), \((\pi, -2)\) and \((3\pi, -2)\).
Exercise \(\PageIndex{4}\)
The following is a graph of slightly more than one period of a sinusoidal function. Six points are labeled on the graph.
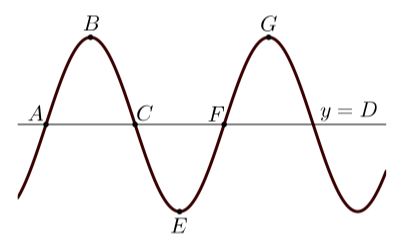
Figure \(\PageIndex{1}\)
For each of the following sinusoidal functions:
- State the amplitude, period, phase shift, and vertical shift.
- State the coordinates of the points \(A, B, C, E, F\), and \(G\). Since the functions are periodic, there are several correct answers. For these functions, make the point \(A\) be as close to the origin as possible.
Notice that the horizontal line is not the horizontal axis but rather, the line \(y = D\).
\[(a) y = 2\sin(\pi x)\]
\[(b) y = 7.2\cos(2x)\]
\[(c) y = 3\sin(x - \dfrac{\pi}{4})\]
\[(d) y = 3\sin(x + \dfrac{\pi}{4})\]
\[(e) y = 4\cos(x - \dfrac{\pi}{3})\]
\[(f) y = 2.8\cos(2(x - \dfrac{\pi}{3}))\]
\[(g) y = 4\sin(2(x - \dfrac{\pi}{4}))+1\]
\[(h) y = -4\cos(2(x + \dfrac{\pi}{4}))+1\]
\[(i) y = 3\cos(2\pi x - \dfrac{\pi}{2})\]
\[(j) y = -1.75\sin(2x - \dfrac{\pi}{3}) + 2\]
\[(k) y = 5\sin(120\pi x)\]
\[(l) y = 40\sin(50\pi(x - \dfrac{1}{100}))\]
- Answer
-
(a) \(y = 2\sin(\pi x)\). The amplitude is \(2\); the period is \(2\); the phase shift is \(0\); and the vertical shift is \(0\).
\[A(0, 0)\] \[B(\dfrac{\pi}{2}, 2)\] \[C(\pi, 0)\] \[E(\dfrac{3\pi}{2}, -2)\] \[F(2\pi, 0)\] \[G(\dfrac{5\pi}{2}, 2)\]
(c) \(y = 3\sin(x - \dfrac{\pi}{4})\). The amplitude is \(3\); the period is \(2\pi\); the phase shift is \(\dfrac{\pi}{4}\); and the vertical shift is \(0\).
\[A(\dfrac{\pi}{4}, 0)\] \[B(\dfrac{3\pi}{4}, 3)\] \[C(\dfrac{5\pi}{4}, 0)\] \[E(\dfrac{7\pi}{4}, -3)\] \[F(\dfrac{7\pi}{4}, -3)\] \[G(\dfrac{11\pi}{4}, 3)\]
(g) \(y = 4\sin(2(x - \dfrac{\pi}{4})) + 1\). The amplitude is \(4\); the period is \(\pi\); the phase shift is \(\dfrac{\pi}{4}\); and the vertical shift is \(1\).
\[A(\dfrac{\pi}{4}, 1)\] \[B(\dfrac{\pi}{2}, 5)\] \[C(\dfrac{3\pi}{4}, 1)\] \[E(\pi, -3)\] \[F(\dfrac{5\pi}{4}, 1)\] \[G(\dfrac{3\pi}{2}, 5)\]
Exercise \(\PageIndex{5}\)
Each of the following graphs is a graph of a sinusoidal function. In each case:
- Determine the amplitude of the sinusoidal function.
- Determine the period of the sinusoidal function.
- Determine the vertical shift of the sinusoidal function.
- Determine an equation of the form \(y = A\sin(B(x - C)) + D\) that produces the given graph.
- Determine an equation of the form \(y = A\cos(B(x - C)) + D\) that produces the given graph.
(a)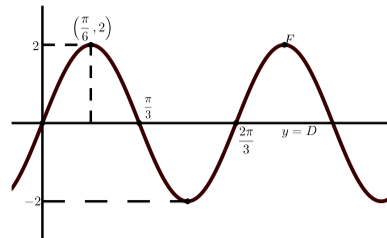
(b)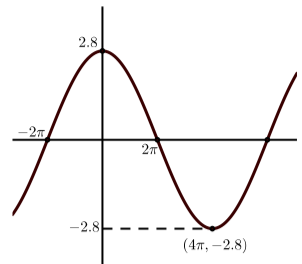
(c)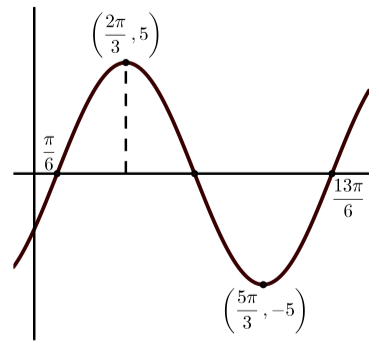
(d)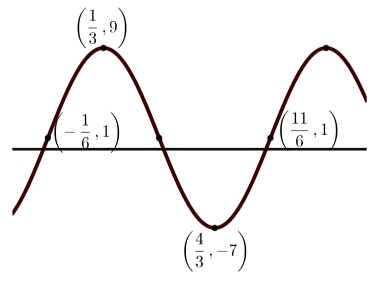
(e)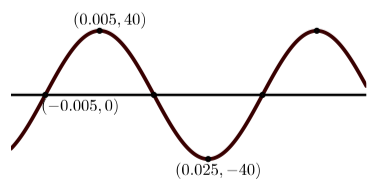
(f)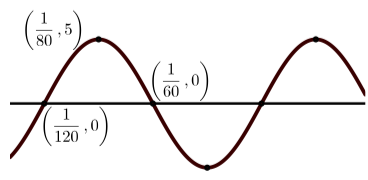
- Answer
-
(a) The amplitude is \(2\); the period is \(\dfrac{2\pi}{3}\); and there is no vertical shift.
For \(y = A\sin(B(x - C)) + D\), there is no phase shift and so \(C = 0\). So \[y = 2\sin(3x)\]. For \(y = A\cos(B(x - C)) + D\), the phase shift is \(\dfrac{\pi}{6}\) and so \(C = \dfrac{\pi}{6}\). So \[y = 2\cos(3(x - \dfrac{\pi}{6}))\].(d) The amplitude is \(8\); the period is \(2\); and the vertical shift is \(1\).
For \(y = A\sin(B(x - C)) + D\), the phase shift is \(-\dfrac{1}{6}\) and so \(C = -\dfrac{1}{6}\). So \[y = 8\sin(\pi(x + \dfrac{1}{6}))\]. For \(y = A\cos(B(x - C)) + D\), the phase shift is \(\dfrac{1}{3}\) and so \(C = \dfrac{1}{3}\). So \[y = 8\cos(\pi(x - \dfrac{1}{3})) + 1\].
Exercise \(\PageIndex{6}\)
Each of the following web links is to an applet on Geogebratube. For each one, the graph of a sinusoidal function is given. The goal is to determine a function of the form
\[f(x) = A\sin(B(x - C)) + D\] or \[f(x) = A\cos(B(x - C)) + D\]
as directed in the applet. There are boxes that must be used to enter the values of \(A, B, C\), and \(D\).
- gvsu.edu/s/09f
- gvsu.edu/s/09g
- http://gvsu.edu/s/09h
- gvsu.edu/s/09i
- gvsu.edu/s/09j
- http://gvsu.edu/s/09k
Exercise \(\PageIndex{7}\)
Determine the amplitude, period, phase shift, and vertical shift for each of the following sinusoids. Then use this information to graph one complete period of the sinusoid and state coordinates of a high point, a low point, and a point where the sinusoid crosses the center line.
\[(a) y = 4\sin(\pi x - \dfrac{\pi}{8})\]
\[(b) y = 5\cos(4x + \dfrac{\pi}{2}) + 2\]
\[(c) y = -3.2\cos(50\pi x - \dfrac{\pi}{2})\]
\[(d) y = 4.8\sin(\dfrac{1}{4}x + \dfrac{\pi}{8})\]
Add text here. For the automatic number to work, you need to add the "AutoNum" template (preferably at the end) to the page.
- Answer
-
(a) We write \(y = 4\sin(\pi x - \dfrac{\pi}{8}) = 4\sin(\pi(x - \dfrac{1}{8}))\). So the amplitude is \(4\), the period is \(2\), the phase shift is \(\dfrac{1}{8}\), and there is no vertical shift.
Some high points on the graph: \((\dfrac{5}{8}, 4)\), \((\dfrac{21}{8}, 4)\). Some low points on the graph: \((\dfrac{13}{8}, -4)\), \((\dfrac{29}{8}, -4)\). Graph crosses the center line at: \((\dfrac{1}{8}, 0)\), \((\dfrac{9}{8}, 0)\), \((\dfrac{17}{8}, 0)\).(b) We write \(y = 4\cos(4x + \dfrac{\pi}{2}) + 2 = 5\cos(4(x + \dfrac{\pi}{8})) + 2\). So the amplitude is \(5\), the period is \(\dfrac{\pi}{2}\), the phase shift is \(-\dfrac{\pi}{8}\), and the vertical shift is \(2\).
Some high points on the graph: \((-\dfrac{\pi}{8}, 7)\), \((\dfrac{3\pi}{8}, 7)\). Some low points on the graph: \((\dfrac{\pi}{8}, -3)\), \((\dfrac{5\pi}{8}, -3)\). Graph crosses the center line at: \((0, 2)\), \((\dfrac{\pi}{4}, 2)\), \((\dfrac{\pi}{2}, 2)\).
Exercise \(\PageIndex{8}\)
Modeling a Heartbeat. For a given person at rest, suppose the heart pumps blood at a regular rate of about 75 pulses per minute. Also, suppose that the volume of this person’s heart is approximately 150 milliliters (ml), and it pushes out about \(54\%\) its volume with each beat. We will model the volume, \(V(t)\)of blood (in milliliters) in the heart at any time \(t\), as a sinusoidal function of the form \[V(t) = A\cos(Bt) + D\]
- If we choose time \(0\) to be a time when the heart is full of blood, why is it reasonable to use a cosine function for our model?
- What is the maximum value of \(V(t)\)? What is the minimum value of (V(t)\)? What does this tell us about the values of A and D? Explain.
- The frequency of a simple harmonic motion is the number of periods per unit time, or the number of pulses per minute in this example. How is the frequency f related to the period? What value should B have? Explain.
- Draw a graph (without a calculator) of your (V(t)\) using your values of A, B, and D, of two periods beginning at \(t = 0\).
- Clearly identify the maximum and minimum values of \(V(t)\)on the graph. What do these numbers tell us about the heart at these times?
- Answer
-
(b) The maximum value is \(150\) ml, and the minimum value is \(81\) ml. So we can use \(A = \dfrac{150 - 81}{2} = 34.5\) and \(D = \dfrac{150 + 81}{2} = 115.5\).
(c) The period is \(\dfrac{1}{75}\) min.
Exercise \(\PageIndex{9}\)
The electricity supplied to residential houses is called alternating current (AC) because the current varies sinusoidally with time. The voltage which causes the current to flow also varies sinusoidally with time. In an alternating (AC) current circuit, the voltage \(V\) (in volts) as a function of time is a sinusoidal function of the form \[V = V_{0}\sin(2\pi ft)\]
where \(V_{0}\) is a positive constant and f is the frequency. The frequency is the number of complete oscillations (cycles) per second. In the United States, fis 60 hertz (Hz), which means that the frequence is 60 cycles per second.
- What is the amplitude and what is the period of the sinusoidal function in (1)? The power (in watts) delivered to a resistance R (in ohms)at any time t is given by \[P = \dfrac{V^2}{R}\]
- Show that \(P = \dfrac{V^2}{R}\sin^2(2\pi ft)\)
- The graph of \(P\) as a function of time is shown below.
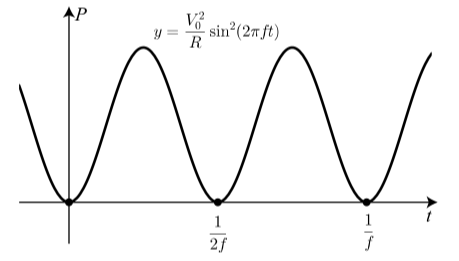
Figure \(\PageIndex{2}\)
Assuming that this shows that \(P\) is a sinusoidal function of t, write \(P\) as a sinusoidal function of time \(t\) by using the negative of a cosine function with no phase shift.
4. So we know that \(P = \dfrac{V_{0}^2}{R}\sin^2(2\pi ft)\) and that P is equal to the sinusoidal function in part (c). Set the two expressions for \(P\) equal to each other and use the resulting equation to conclude that \[sin^2(2\pi ft) = \dfrac{1}{2}[1 - cos(4\pi ft)]\]
Exercise \(\PageIndex{10}\)
The electricity supplied to residential houses is called alternating current (AC) because the current varies sinusoidally with time. The voltage which causes the current to flow also varies sinusoidally with time. Both current and voltage have a frequency of 60 cycles per second, but they have different phase shifts. (Note: A frequency of 60 cycles per second corresponds to a period of \(\dfrac{1}{60}\) of a second.)
Let \(C\) be the current (in amperes), let \(V\) be the voltage (in volts), and let t be time (in seconds). The following list gives information that is known about \(C\) and \(V\).
- The current \(C\) is a sinusoidal function of time with a frequency of 60 cycles per second, and it reaches its maximum of 5 amperes when \(t = 0\) seconds.
- The voltage \(V\) is a sinusoidal function of time with a frequency of 60 cycles per second. As shown in the graphs on the next page, \(V\) “leads” the current in the sense that it reaches its maximum before the current reaches its maximum. (“Leading” corresponds to a negative phase shift, and “lagging” corresponds to a positive phase shift.) In this case, the voltage V leads the current by 0.003 seconds, meaning that it reaches its maximum 0.003 seconds before the current reaches its maximum.
- The peak voltage is 180 volts.
- There is no vertical shift on either the current or the voltage graph.
- Determine sinusoidal functions for both \(C\) and \(V\).
- What is the voltage when the current is a maximum?
- What is the current when the voltage is a minimum?
- What is the current when the voltage is equal to zero?
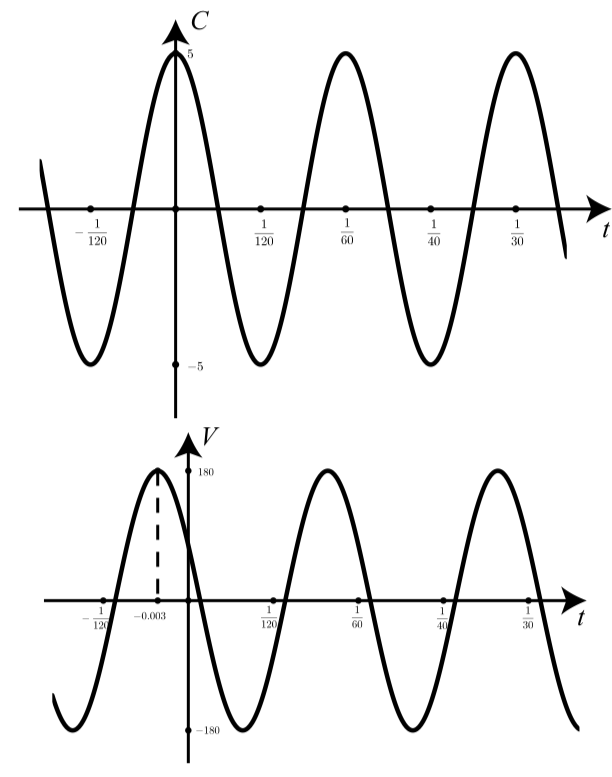
Figure \(\PageIndex{3}\): Current \(C\) and Voltage \(V\) As Functions of Time
Exercise \(\PageIndex{11}\)
We will let \(t\) be the number of the day of the year. The following table shows sunrise times (in minutes since midnight) for certain days of the year at Houghton, Michigan.
| day | 1 | 31 | 61 | 91 | 121 | 151 | 181 | 211 | 241 | 271 | 301 | 331 | 361 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| time | 521 | 501 | 453 | 394 | 339 | 304 | 302 | 330 | 369 | 408 | 451 | 494 | 520 |
The points for this table are plotted on the following graph.
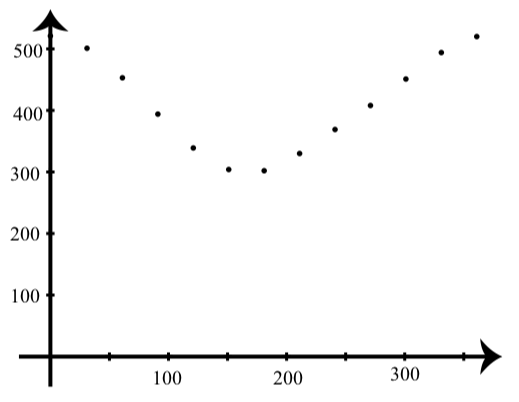
Figure \(\PageIndex{4}\)
- Let \(t\) be the number of the day of the year and let \(y\) be the the sunrise time in minutes since midnight at Houghton, MI. Determine a sinusoidal model for \(y\) as a function of \(t\).
- To check the work in Part(a), use a graphing utility or Geogebra to plot the points in the table and superimpose the graph of the function from Part (a).
- Use Geogebra to determine a sinusoidal model for \(y\) as a function of \(t\). This model will be in the form \(y = a\sin(bt + c) + d\), where \(a, b, c\), and \(d\) are real numbers.
- Determine the amplitude, period, phase shift, and vertical shift for the sinusoidal model in Part (c).
Exercise \(\PageIndex{12}\)
Modeling the Distance from the Earth to the Sun.
The Earth’s orbit around the sun is not a perfect circle. In 1609 Johannes Kepler published two of his famous laws of planetary motion, one of which states that planetary orbits are actually ellipses. So the distance from the Earth to the sun is not a constant, but varies over the course of its orbit (we will assume a 365 day year). According to the 1996 US Ephemeris, the distances from the sun to the Earth on the 21st of each month are given in Table 2.3. The distances are measured in Astronomical Units (AU), where 1 AU is approximately \(149597900\) kilometers.
http://image.gsfc.nasa.gov/poetry/venus/q638.html
| Month | Day of the year | Distance |
|---|---|---|
| January | 21 | 0.9840 |
| February | 52 | 0.9888 |
| March | 80 | 0.9962 |
| April | 111 | 1.0050 |
| May | 141 | 1.0122 |
| June | 172 | 1.0163 |
July |
202 | 1.0161 |
| August | 233 | 1.0116 |
| September | 264 | 1.0039 |
| October | 294 | 0.9954 |
| November | 325 | 0.9878 |
| December | 355 | 0.9837 |
Table \(\PageIndex{1}\): Distances from the Earth to the sun on the 21st of each month
A plot of this data with the day of the year along the horizontal axis and the distance from the Earth to the sun on the vertical axis is given in Figure \(\PageIndex{5}\).
We will use a sinusoidal function to model this data. That is, we will let \(f(t)\) be the distance from the Earth to the Sun on day \(t\) of the year and that \[f(t) = A\sin(B(t - C)) + D\]
- What are the maximum and minimum distances from the Earth to the sun given by the data? What does this tell us about the amplitude off.t/? Use this to approximate the values of \(A\) and \(D\) in the model function \(f\)? What is the center line for this sinusoidal model?
- The period of this sinusoidal function is 365 days. What is the value of \(B\) for this sinusoidal function?
- Draw the center line you found in part (a) on the plot of the data in Figure \(\PageIndex{5}\). At approximately what value of \(t\) will the graph of fintersect this center line? How is this number related to the phase shift of the data? What is the value of \(C\) for this sinusoidal function?
- Use Geogebra to plot the points from the data in Table \(\PageIndex{1}\) and then use Geogebra to draw the graph of the sinusoidal model \(f(t) = A\sin(B(t - C)) + D\). Does this function model the data reasonably well?
- Use the sinusoidal model \(f(t) = A\sin(B(t - C)) + D\) to estimate the distance from the Earth to the Sun on July 4.
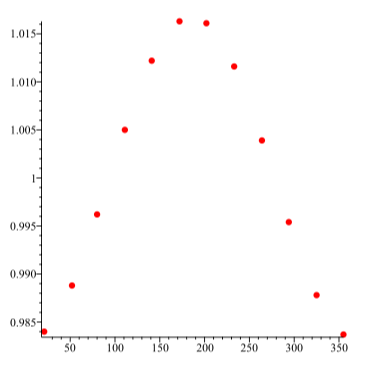
Figure \(\PageIndex{5}\): Distance from the Earth to the sun as a function of the day of the year
Exercise \(\PageIndex{13}\)
Continuation of Exercise \(\PageIndex{12}\).
Use Geogebra to plot the points from the data in Table \(\PageIndex{1}\). Then use the “FitSin” command in Geogebra to find a sinusoidal model for this data of the form \(g(t) = a\sin(bt + c) + d\)
What is the amplitude of this sinusoidal model? What is the period? What is the horizontal shift? What is the phase shift?
How do these values compare with the corresponding values for the sinusoid \(f(t) = A\sin(B(t - C)) + D\) obtained in Exercise (6)?
Exercise \(\PageIndex{14}\)
As the moon orbits the earth, the appearance of the moon changes. We see various lunar disks at different times of the month. These changes reappear during each lunar month. However, a lunar month is not exactly the same as the twelve months we use in our calendar today. A lunar month is the number of days it takes the moon to go through one complete cycle from a full moon (100% illumination) to the next full moon.
The following data were gathered from the web site for the U.S. Naval Observatory. The data are the percent of the moon that is illuminated is geocentric value of the percent of the moon that is illuminated. That is, the percent of illumination is computed for a fictitious observer located at the center of the Earth.
| Date | Percent Illuminated |
|---|---|
| 3/1/2013 | \(87\%\) |
| 3/3/2013 | \(69\%\) |
| 3/5/2017 | \(47\%\) |
| 3/7/2017 | \(25\%\) |
| 3/9/2017 | \(9\%\) |
| 3/12/2013 | \(0\%\) |
| 3/13/2013 | \(2\%\) |
| 3/15/2017 | \(12\%\) |
| 3/17/2013 | \(27\%\) |
| 3/19/2013 | \(45\%\) |
| 3/21/2013 | \(64\%\) |
| 3/23/2013 | \(81\%\) |
| 3/25/2013 | \(94\%\) |
| 3/27/2013 | \(100\%\) |
| 3/29/2013 | \(96\%\) |
Table \(\PageIndex{2}\)
- Determine a sinusoidal function of the form \(y = A\cos(B(t - C)) + D\) to model this data. For this function, let x be the number of days since the beginning of March 2017 and let y be the percent of the moon that is illuminated. What is the amplitude, period, phase shift, and vertical shift of this sinusoidal function?
- Use Geogebra to draw a scatter plot of this data and superimpose the graph of the function from part (a).
- Use Geogebra to determine a sinusoidal function of the form \(y = A\sin(Bx + K) + D\) to model this data and superimpose its graph on the scatter plot. What is the amplitude, period, phase shift, and vertical shift of this sinusoidal function?
Exercise \(\PageIndex{15}\)
Each of the following web links is to an applet on Geogebratube. For each one, data is plotted and in some cases, the actual data is shown in a spread-sheet on the right. The goal is to determine a function of the form
\[f(x) = A\sin(B(x- C)) + D\] or \[f(x) = A\cos(B(x- C)) + D\]
that fits the data as closely as possible. Each applet will state which type of function to use. There are boxes that must be used to enter the values of \(A, B, C\), and \(D\).
- gvsu.edu/s/09l
- http://gvsu.edu/s/09m
- http://gvsu.edu/s/09n
- http://gvsu.edu/s/09o
Exercise \(\PageIndex{16}\)
In this exercise, we will explore the period of the tangent function.
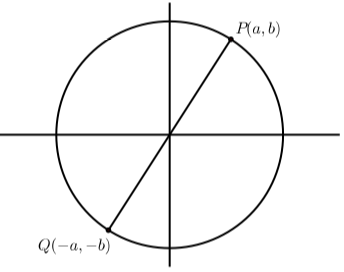
Figure \(\PageIndex{6}\)
- Use the definition of the tangent function and the fact that the period of both the sine and cosine functions is equal to \(2\pi\) to prove that for any real number t in the domain of the tangent function, \[\tan(t + 2\pi) = \tan(t)\] However, this does not prove that the period of the tangent function is equal to \(2\pi\). We will now show that the period is equal to \(\pi\). The key to the proof is the diagram to the right. Suppose that \(P\) is the terminal point of the arc \(t\). So \(\cos(t) = a\) and \(\sin(t) = b\). The diagram shows a point Q that is the terminal point of the arc \(t + \pi\). By the symmetry of the circle, we know that the point \(Q\) has coordinates \((-a, -b)\).
- Explain why \(\cos(t + \pi) = -a\) and \(\sin(t + \pi) = -b\)
- Use the information in part(1) and the definition of the tangent function to prove that \(\tan(t + \pi) = \tan(t)\).
The diagram also indicates that the smallest positive value of \(p\) for which \(\tan(t + p) = \tan(t)\) must be \(p = \pi\). Hence, the period the tangent function is equal to \(\pi\).
Exercise \(\PageIndex{17}\)
We have seen that \(\cos(-t) = \cos(t)\) and \(\sin(-t) = \sin(t)\) for every real number \(t\). Now assume that \(t\) is a real number for which \(\tan(t)\) is defined.
- Use the definition of the tangent function to write a formula for \(\tan(-t)\) in terms of \(\sin(-t)\) and \(\cos(-t)\).
- Now use the negative arc identities for the cosine and sine functions to help prove that \(\tan(-t) = -\tan(t)\). This is called the negative arc identity for the tangent function.
- Use the negative arc identity for the tangent function to explain why the graph of \(y = \tan(t)\) is symmetric about the origin.
Exercise \(\PageIndex{18}\)
Use the negative arc identities for sine, cosine, and tangent to help prove the following negative arc identities for cosecant, secant, and cotangent.
- For every real number \(t\) for which \(t \neq k\pi\) for every integer \(k\), \(\csc(-t) = -\csc(t)\).
- For every real number \(t\) for which \(t \neq \dfrac{\pi}{2} + k\pi\) for every integer \(k\), \(\sec(-t) = \sec(t)\).
- For every real number \(t\) for which \(t \neq k\pi\) for every integer \(k\), \(\cot(-t) = -\cot(t)\).
Exercise \(\PageIndex{19}\)
The Cosecant Function.
If necessary, refer to Section 1.6 to answer the following questions.
- How is the cosecant function defined?
- What is the domain of the cosecant function?
- Where will the graph of the cosecant function have vertical asymptotes?
- What is the period of the cosecant function?
Exercise \(\PageIndex{20}\)
Exploring the Graph of the Cosecant Function.
- Use the Geogebra Applet with the following web address to explore the relationship between the graph of the cosecant function and the sine function. http://gvsu.edu/s/0bH In the applet, the graph of \(y = \sin(t)\) is shown and is left fixed. Points on the graph of \(y = \csc(t)\) are generated by using the slider for \(t\). For each value of \(t\), a vertical line is drawn from the point \((t, \sin(t))\) to the point \((t, \csc(t))\). Notice how these points indicate that the graph of the cosecant function has vertical asymptotes at \(t = 0, t = \pi\) and \(t = 2\pi\).
- Use a graphing utility to draw the graph of \(y = \csc(t)\) using \(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\) and \(-10 \leq y \leq 10\). Note: It may be necessary to use \(\csc(x) = \dfrac{1}{\sin(x)}\)
- Use a graphing utility to draw the graph of \(y = \csc(t)\) using \(-\dfrac{3\pi}{2} \leq x \leq \dfrac{3\pi}{2}\) and \(-10 \leq y \leq 10\).
Exercise \(\PageIndex{21}\)
The Graph of the Cosecant Function.
- Why does the graph of \(y = \csc(t)\) have vertical asymptotes at \(x = 0, x = \pi\), and \(x = 2\pi\)? What is the domain of the cosecant function?
- Why is the graph of \(y = \csc(t)\) above the x-axis when \(0 < x < \pi\)?
- Why is the graph of \(y = \csc(t)\) above the x-axis when \(\pi < x < 2\pi\)?
- What is the range of the cosecant function?
Exercise \(\PageIndex{22}\)
The Cotangent Function.
If necessary, refer to Section 1.6 to answer the following questions.
- How is the cotangent function defined?
- What is the domain of the cotangent function?
- Where will the graph of the cotangent function have vertical asymptotes?
- What is the period of the cotangent function?
Exercise \(\PageIndex{23}\)
Exploring the Graph of the Cotangent Function.
- Use a graphing utility to draw the graph of \(y = \cot(x)\) using \(-\pi \leq x \leq \pi\) and \(-10 \leq y \leq 10\). Note: It may be necessary to use \(\cot(x) = \dfrac{1}{tan(x)}\).
- Use a graphing utility to draw the graph of \(y = \cot(x)\) using \(-2\pi \leq x \leq 2\pi\) and \(-10 \leq y \leq 10\).
Exercise \(\PageIndex{24}\)
The Graph of the Cotangent Function.
- Why does the graph of \(y = \cot(t)\) have vertical asymptotes at \(x = 0, x = \pi\), and \(x = 2\pi\)? What is the domain of the cosecant function?
- Why is the graph of \(y = \cot(t)\) above the x-axis when \(0 < x < \dfrac{\pi}{2}\) and when \(\pi < x < \dfrac{3\pi}{2}\)?
- Why is the graph of \(y = \cot(t)\) above the x-axis when \(\dfrac{\pi}{2} < x < \pi\) and when \(\dfrac{3\pi}{2} < x < 2\pi\)?
- What is the range of the cotangent function?
Exercise \(\PageIndex{25}\)
Rewrite each of the following using the corresponding trigonometric function for the inverse trigonometric function. Then determine the exact value of the inverse trigonometric function.
\[(a) t = \arcsin(\dfrac{\sqrt{2}}{2})\]
\[(b) t = \arcsin(-\dfrac{\sqrt{2}}{2})\]
\[(c) t = \arccos(\dfrac{\sqrt{2}}{2})\]
\[(d) t = \arccos(-\dfrac{\sqrt{2}}{2})\]
\[(e) y = \tan^{-1}(\dfrac{\sqrt{3}}{2})\]
\[(f) y = \tan^{-1}(\dfrac{-\sqrt{3}}{2})\]
\[(g) y = \cos^{-1}(0)\]
\[(h) t = \arctan(0)\]
\[(i) y = \sin^{-1}(-\dfrac{1}{2})\]
\[(j) y = \cos^{-1}(-\dfrac{1}{2})\]
- Answer
-
(a) \(t = \arcsin(\dfrac{\sqrt{2}}{2})\) means \(\sin(t) = \dfrac{\sqrt{2}}{2}\) and \(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\). Since \(\sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}\), we see that \(t = \arcsin(\dfrac{\sqrt{2}}{2}) = \dfrac{\pi}{4}\).
(b) \(t = \arcsin(-\dfrac{\sqrt{2}}{2})\) means \(\sin(t) = -\dfrac{\sqrt{2}}{2}\) and \(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\). Since \(\sin(\dfrac{-\pi}{4}) = -\dfrac{\sqrt{2}}{2}\), we see that \(t = \arcsin(\dfrac{\sqrt{2}}{2}) = -\dfrac{\pi}{4}\).
(d) \(t = \arccos(-\dfrac{\sqrt{2}}{2})\) means \(\cos(t) = -\dfrac{\sqrt{2}}{2}\) and \(0 \leq t \leq \pi\). Since \(\cos(\dfrac{3\pi}{4}) = -\dfrac{\sqrt{2}}{2}\), we see that \(t = \arccos(\dfrac{\sqrt{2}}{2}) = \dfrac{3\pi}{4}\).
(f) \(y = \tan^{-1}(-\dfrac{\sqrt{3}}{3})\) means \(\tan(y) = -\dfrac{\sqrt{3}}{3}\) and \(-\dfrac{\pi}{2} < y < \dfrac{\pi}{2}\). Since \(\tan(-\dfrac{\pi}{6}) = -\dfrac{\sqrt{3}}{3}\), we see that \(y = \tan^{-1}(-\dfrac{\sqrt{3}}{2}) = -\dfrac{\pi}{6}\).
(h) \(t = \arctan(0) = 0\)
(j) \(y = \cos^{-1}(-\dfrac{1}{2}) = \dfrac{2\pi}{3}\).
Exercise \(\PageIndex{26}\)
Determine the exact value of each of the following expressions.
\[(a) \sin(\sin^{-1}(1))\]
\[(b) \sin^{-1}(\sin(\dfrac{\pi}{3}))\]
\[(c) \cos^{-1}(\sin(\dfrac{\pi}{3}))\]
\[(d) \sin^{-1}(\sin(-\dfrac{\pi}{3}))\]
\[(e) \cos^{-1}(\cos(-\dfrac{\pi}{3}))\]
\[(f) \arcsin(\sin(\dfrac{2\pi}{3}))\]
\[(g) \tan(\arctan(1))\]
\[(h) \arctan(\tan(\dfrac{\pi}{4}))\]
\[(i) \arctan(\tan(\dfrac{3\pi}{4}))\]
- Answer
-
(a) \(\sin(\sin^{-1}(1)) = \sin(\dfrac{\pi}{2}) = 1\)
(b) \(\sin^{-1}(\sin(\dfrac{\pi}{3})) = \sin^{-1}(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\)
(e) \(\cos^{-1}(\cos(-\dfrac{\pi}{3})) = \cos^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{3}\)
(f) \(\arcsin(\sin(\dfrac{2\pi}{3})) = \arcsin(\dfrac{\sqrt{3}}{2}) = \dfrac{\pi}{3}\)
(i) \(\arctan(\tan(\dfrac{3\pi}{4})) = \arctan(-1) = -\dfrac{\pi}{4}\)
Exercise \(\PageIndex{27}\)
Determine the exact value of each of the following expressions.
\[(a) \cos(\arcsin(\dfrac{2}{5}))\]
\[(b) \sin(\arccos(-\dfrac{2}{3}))\]
\[(c) \tan(\arcsin(\dfrac{1}{3}))\]
\[(d) \cos(\arcsin(-\dfrac{2}{5}))\]
\[(e) \tan(\arccos(-\dfrac{2}{9}))\]
- Answer
-
(a) Let \(t = \arcsin(\dfrac{2}{5})\). Then \(\sin(t) = \dfrac{2}{5}\) and \(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\), and
\[\cos^{2}(t) + \sin^{2}(t) = 1\]
\[\cos^{2}(t) + \dfrac{4}{25} = 1\]
\[\cos^{2}(t) = \dfrac{21}{25}\]
Since \(-\dfrac{\pi}{2} \leq t \leq \dfrac{\pi}{2}\), we know that \(\cos(t) \geq 0\). Hence, \(\cos(t) = \dfrac{\sqrt{21}}{5}\) and \(\cos(\arcsin(\dfrac{2}{5})) = \dfrac{\sqrt{21}}{5}\).
(b) \(\sin(\arccos(-\dfrac{2}{3})) = \dfrac{\sqrt{5}}{3}\).
(c) \(\tan(\arcsin(\dfrac{1}{3})) = \dfrac{1}{\sqrt{8}}\).
Exercise \(\PageIndex{28}\)
This exercise provides a justification for the properties of the inverse cosine function on page 150. Let \(t\) be a real number in the closed interval \([0, \pi]\) and let \[y = \cos(t).\] We then see that \(-1 \leq y \leq 1\) and \[\cos^{-1}(y) = t\]
- Use the equations to rewrite the expression \(\cos^{-1}(\cos(t))\).
- Use the equations to rewrite the expression \(\cos(\cos^{-1}(y))\).
Exercise \(\PageIndex{29}\)
This exercise provides a justification for the properties of the inverse cosine function on page 151. Let \(t\) be a real number in the open interval \((-\dfrac{\pi}{2}, \dfrac{\pi}{2})\) and let \[y = \tan(t).\] We then see that \(y\) is a real number and \[\tan^{-1}(y) = t\]
- Use the equations to rewrite the expression \(\tan^{-1}(\tan(t))\).
- Use the equations to rewrite the expression \(\tan(\tan^{-1}(y))\).
Exercise \(\PageIndex{30}\)
For each of the following equations, use a graph to approximate the solutions (to three decimal places) of the equation on the indicated interval. Then use the periodic property of the trigonometric function to write formulas that can be used to approximate any solution of the given equation.
- \(\sin(x) = 0.75\) with \(-\pi \leq x \leq \pi\)
- \(\cos(x) = 0.75\) with \(-\pi \leq x \leq \pi\)
- \(\tan(x) = 0.75\) with \((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\)
- \(\sin(x) = -0.75\) with \(-\pi \leq x \leq \pi\)
- \(\cos(x) = -0.75\) with \(-\pi \leq x \leq \pi\)
- \(\tan(x) = -0.75\) with \((-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2})\)
- Answer
-
(a) \(x = 0.848 + k(2\pi)\) or \(x = 2.294 + k(2\pi)\), where \(k\) is an integer.
(d) \(x = -0.848 + k(2\pi)\) or \(x = -2.294 + k(2\pi)\), where \(k\) is an integer.
Exercise \(\PageIndex{31}\)
For each of the equations in Exercise (1), use an inverse trigonometric function to write the exact values of all the solutions of the equation on the indicated interval. Then use the periodic property of the trigonometric function to write formulas that can be used to generate all of the solutions of the given equation.
- Answer
-
(a) \(x = \sin^{-1}(0.75) + k(2\pi)\) or \(x = (\pi - \sin^{-1}(0.75)) + k(2\pi)\), where \(k\) is an integer.
(d) \(x = \arcsin(-0.75) + k(2\pi)\) or \(x = (\pi - \arcsin(-0.75)) + k(2\pi)\), where \(k\) is an integer.
Exercise \(\PageIndex{32}\)
For each of the equations of the following equations, use an inverse trigonometric function to write the exact values of all the solutions of the equation on the indicated interval. Then use the periodic property of the trigonometric function to write formulas that can be used to generate all of the solutions of the given equation.
- \(\sin(x) + 2 = 2.4\) with \(-\pi \leq x \leq \pi\)
- \(5\cos(x) + 3 = 7\) with \(-\pi \leq x \leq \pi\)
- \(2\tan(x) + 4 = 10\) with \(-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}\)
- \(-3.8\sin(x) + 7 = 10\) with \(-\pi \leq x \leq \pi\)
- \(8\cos(x) + 7 = 2\) with \(-\pi \leq x \leq \pi\)
- Answer
-
(a) \(x = \sin^{-1}(0.4) + k(2\pi)\) or \(x = (\pi - \sin^{-1}(0.4)) + k(2\pi)\), where \(k\) is an integer.
(b) \(x = \cos^{-1}(\dfrac{4}{5}) + k(2\pi)\) or \(x = -\cos^{-1}(\dfrac{4}{5}) + k(2\pi)\), where \(k\) is an integer.
Exercise \(\PageIndex{33}\)
Determine the exact values of the solutions of the given equation on one complete period of the trigonometric function that is used in the equation. Then use the periodic property of the trigonometric function to write formulas that can be used to all of the solutions of the given equation.
- \(4\sin(2x) = 3\)
- \(4\cos(2x) = 3\)
- \(\cos(\pi x) = 0.6\)
- \(\sin(\pi x - \dfrac{\pi}{4}) = 0.2\)
- \(\cos(\pi x - \dfrac{\pi}{4}) = 0.2\)
- Answer
-
(a) The period for the trigonometric function is \(\pi\). We first solve the equation \(4\sin(t) = 3\) with \(-\pi \leq t \leq \pi\) and obtain \(t = \sin^{-1}(0.75) + k(2\pi)\) or \(t = (\pi - \sin^{-1}(0.75)) + k(2\pi)\). We then use the substitution \(t = 2x\) to obtain \(x = \dfrac{1}{2}\sin^{-1}(0.75) + k\pi\) or \(x = \dfrac{1}{2}(\pi - \sin^{-1}(0.75)) + k\pi\), where \(k\) is an integer.
(d) The period for the trigonometric function is \(2\). We first solve the equation \(\sin(t) = 0.2\) with \(-\pi \leq t \leq \pi\) and obtain \(t = \sin^{-1}(0.2) + k(2\pi)\) or \(t = (\pi - \sin^{-1}(0.2)) + k(2\pi)\). We now use the substitution \(t = \pi x - \dfrac{\pi}{4}\) to obtain \(x = \dfrac{1}{\pi}\sin^{-1}(0.2) + \dfrac{1}{4}\) or \(x = -\dfrac{1}{\pi} + \dfrac{5}{4}) + 2k\), where \(k\) is an integer.
Exercise \(\PageIndex{34}\)
In Example 2.17 on page 2.17, we used graphical methods to find two solutions of the equation \[35\cos(\dfrac{5\pi}{3}t) + 105 = 100\]
We found that two solutions were \(t \approx 0.3274\) and \(t \approx 0.8726\). Rewrite this equation and then use the inverse cosine function to determine the exact values of these two solutions. Then use the period of the function \(35\cos(\dfrac{5\pi}{3}t) + 105\) to write formulas that can be used to generate all of the solutions of the given equation.

