3.3: Triangles that are Not Right Triangles

Last updated
Save as PDF

Page ID: 7113

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Focus Questions

The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.

What is the Law of Sines?
What information do we need about a triangle to apply the Law of Sines?
What do we mean by the ambiguous case for the Law of Sines? Why is it ambiguous?
What is the Law of Cosines?
What information do we need about a triangle to apply the Law of Cosines?

In Section 3.2, we learned how to use the trigonometric functions and given information about a right triangle to determine other parts of that right triangle. Of course, there are many triangles without right angles (these triangles are called oblique triangles). Our next task is to develop methods to relate sides and angles of oblique triangles. In this section, we will develop two such methods, the Law of Sines and the Law of Cosines. In the next section, we will learn how to use these methods in applications.

As with right triangles, we will want some standard notation when working with general triangles. Our notation will be similar to the what we used for right triangles. In particular, we will often let the lengths of the three sides of a triangle be $a$, $b$, and $c$. The angles opposite the sides of length $a$, $b$, and $c$ will be labeled $\alpha$, $\beta$, and $\gamma$ respectively (Figure $\PageIndex{1}$).

We will sometimes label the vertices of the triangle as A, B, and C as shown in Figure $\PageIndex{1}$.

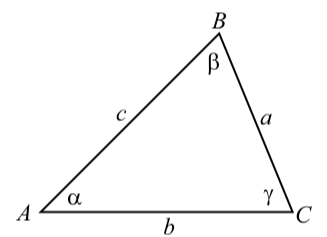
$3.12.png$

Figure $\PageIndex{1}$: Standard Labeling for a Triangle

Beginning Activity

Before we state the Law of Sines and the Law of Cosines, we are going to use two Geogebra apps to explore the relationships about the parts of a triangle. In each of these apps, a triangle is drawn. The lengths of the sides of the triangle and the measure for each of the angles in shown. The size and shape of the triangle can be changed by dragging one (or all) of the points that form the vertices of the triangle.

1. Open the Geogebra app called The Law of Sines at http://gvsu.edu/s/01B

Experiment by moving the vertices of the triangle and observing what happens with the lengths and the angles and the computations shown in the lower left part of the screen.
Use a particular triangle and verify the computations shown in the lower left part of the screen. Round your results to the nearest thousandth as is done in the app.
Write an equation (or equations) that this app is illustrating. This will be part of the Law of Sines.

2. Open the Geogebra app called The Law of Cosines at http://gvsu.edu/s/01C

Experiment by moving the vertices of the triangle and observing what happens with the lengths and the angles and the computations shown in the lower left part of the screen.
Use a particular triangle and verify the computations shown in the lower left part of the screen. Round your results to the nearest thousandth as is done in the app.
Write an equation that this app is illustrating. This will be part of the Law of Cosines.

The Law of Sines

The first part of the beginning activity was meant to illustrate the Law of Sines. Following is a formal statement of the Law of Sines.

Law of Sines

In a triangle, if $a$, $b$, and $c$ are the lengths of the sides opposite angles $\alpha$, $\beta$, and $\gamma$, respectively, then

\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c}\]

This is equivalent to

\[\dfrac{a}{\sin(\alpha)} = \dfrac{b}{\sin(\beta)} = \dfrac{c}{\sin(\gamma)}\]

Please note that the Law of Sines actually has three equations condensed into a single line. The three equations are:

\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b}\]\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\gamma)}{c}\]\[\dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c}\]

The key to using the Law of Sines is that each equation involves 4 quantities, and if we know 3 of these quantities, we can use the Law of Sines to determine the fourth. These 4 quantities are actually two different pairs, where one element of a pair is an angle and the other element of that pair is the length of the side opposite that angle. In Figure $\PageIndex{2}$, $\theta$ and $x$ form one such pair, and $\phi$ and $y$ are another such pair. We can write the Law of Sines as follows:

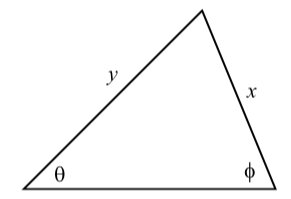
$3.13.png$

Figure $\PageIndex{2}$: Diagram for the Law of Sines

Law of Sines

In a triangle, if $x$ is the length of the side opposite angle $\theta$ and $y$ is the length of the side opposite angle $\phi$, then

\[\dfrac{x}{\sin(\theta)} = \dfrac{y}{\sin(\phi)}\]or \[\dfrac{\sin(\theta)}{x} = \dfrac{\sin(\phi)}{y}. \label{lawofsines}\]

Example $\PageIndex{1}$: Using the Law of Sines

Suppose that the measures of two angles of a triangle are $25^\circ$ and $51.3^\circ$ and that the side opposite the $25^\circ$ angle is 12 feet long. We will use the Law of Sines to determine the other three parts of the triangle. (Remember that we often say that we are “solving the triangle.”) The first step is to draw a reasonable accurate diagram of the triangle and label the parts. This is shown in the following diagram.

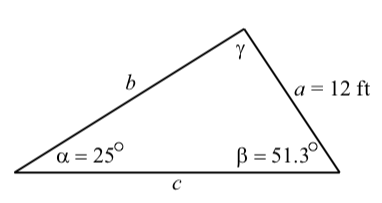
$example 3.13.png$

We notice that we know the values of the length of a side and its opposite angles ($a$ and $\alpha$). Since we also know the value of $\beta$, we can use the Law of Sines to determine $b$. This is done as follows:

\[\dfrac{a}{\sin(\alpha)} = \dfrac{b}{\sin(\beta)}\]\[b = \dfrac{a\sin(\beta)}{\sin(\alpha)}\]\[b = \dfrac{12\sin(51.3^\circ)}{\sin(25^\circ)}\]\[b \approx 22.160\]

So we see that the side opposite the $51.3^\circ$ angle is about 22.160 feet in length. We still need to determine $\gamma$ and $c$. We will use the fact that the sum of the angles of a triangle is equal to $180^\circ$ to determine $\gamma$.
Now that we know $\gamma$, we can use the Law of Sines again to determine $c$. To do this, we solve the following equation for $c$.

\[\dfrac{a}{\sin(\alpha)} = \dfrac{c}{\sin(\gamma)}\]

We should verify that the result is $c \approx 27.587$ feet. To check our results, we should verify that for this triangle, \[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c} \approx 0.035.\]

Exercise $\PageIndex{1}$

Suppose that the measures of two angles of a triangle are $15^\circ$ and $135^\circ$ and that the side that is common to these two angles is $71$ inches long. Following is a reasonably accurate diagram for this triangle.

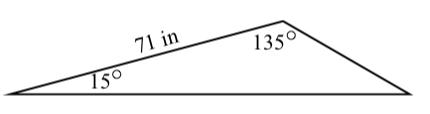
$pc 3.14.png$

Determine the lengths of the other two sides of the triangle and the measure of the third angle. Hint: First introduce some appropriate notation, determine the measure of the third angle, and then use the Law of Sines.

Answer

We first note that the third angle in the triangle is $30^\circ$ since the sum of the two given angles is $150^\circ$. We let x be the length of the side opposite the $15^\circ$ angle and let $y$ be the length of the side opposite the $135^\circ$ angle. We then see that

\[\dfrac{x}{\sin(15^\circ)} = \dfrac{71}{\sin(30^\circ)}\]
\[x = \dfrac{71\sin(15^\circ)}{\sin(30^\circ)}\]
\[x \approx 36.752\]

\[\dfrac{y}{\sin(135^\circ)} = \dfrac{71}{\sin(30^\circ)}\]
\[y = \dfrac{71\sin(135^\circ)}{\sin(30^\circ)}\]
\[y \approx 100.409\]

So the length of the side opposite the $15^\circ$ angle is about $36.75$ inches, and the length of the side opposite the $135^\circ$ angle is about $100.41$ inches.

Using the Law of Sines to Determine an Angle

As we have stated, an equation for the Law of Sines involves four quantities, two angles and the lengths of the two sides opposite these angles. In the examples we have looked at, two angles and one side has been given. We then used the Law of Sines to determine the length of the other side.

We can run into a slight complication when we want to determine an angle using the Law of Sines. This can occur when we are given the lengths of two sides and the measure of an angle opposite one of these sides. The problem is that there are two different angles between $0^\circ$ and $180^\circ$ that are solutions of an equation of the form $\sin(\theta) = $ "a number between $0$ and $1$".
For example, consider the equation $\sin(\theta) = 0.7$. We can use the inverse sine function to determine one solution of this equation, which is \[\theta_{1} = \sin^{-1}(0.7) \approx 44.427^\circ.\]

The inverse sine function gives us the solution that is between $0^\circ$ and $90^\circ$, that is, the solution in the first quadrant. There is a second solution to this equation in the second quadrant, that is, between $90^\circ$ and $180^\circ$. This second solution is $\theta_{2} = 180^\circ - \theta_{1}$. So in this case, \[\theta_{2} = 180^\circ - \sin^{-1}(0.7) \approx 135.573^\circ.\]
The next two progress checks will be guided activities through examples where we will need to use the Law of Sines to determine an angle.

Exercise $\PageIndex{2}$

Suppose a triangle has a side of length $2$ feet that is an adjacent side for an angle of $40^\circ$. Is it possible for the side opposite the $40^\circ$ angle to have a length of $1.7$ feet?

To try to answer this, we first draw a reasonably accurate diagram of the situation as shown below.

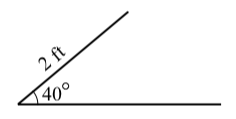
$pc 3.15.png$

The horizontal line is not a side of the triangle (yet). For now, we are just using it as one of the sides of the $40^\circ$ angle. In addition, we have not drawn the side opposite the $40^\circ$ angle since just by observation, it appears there could be two possible ways to draw a side of length 3 feet. Now we get to the details.

Let $\theta$ be the angle opposite the side of length 2 feet. Use the Law of Sines to determine $\sin(\theta)$.
Use the inverse sine function to determine one solution (rounded to the nearest tenth of a degree) for $\theta$. Call this solution $\theta_{1}$.
Let $\theta_{2} = 180^\circ - \theta_{1}$ Explain why (or verify that) $\theta_{2}$ is also a solution of the equation in part (1).

This means that there could be two triangles that satisfy the conditions of the problem.

Determine the third angle and the third side when the angle opposite the side of length $2$ is $\theta_{1}$.
Determine the third angle and the third side when the angle opposite the side of length $2$ is $\theta_{2}$.

Answer

1. The side opposite the angle of $40^\circ$ has length $1.7$ feet. So we get

\[\dfrac{\sin(\theta)}{2} = \dfrac{\sin(40^\circ)}{1.7}\]
\[\sin(\theta) = \dfrac{2\sin(40^\circ)}{1.7} \approx 0.75622\]
2. We see that

\[\theta_{1} = \sin^{-1}(\dfrac{2\sin(40^\circ)}{1.7}) \approx 49.132^\circ\]

3. $\theta_{2} = 180^\circ - \theta_{1} \approx 130.868^\circ$. Using reference angles instead of reference arcs, $\theta_{1}$ is the reference angle for $\theta_{2}$, which is in the second quadrant. Hence, $\sin(\theta_{2}) = \sin(\theta_{1})$

4. The third angle $\alpha$ can be determined using the sum of the angles of a triangle.

\[\alpha + \theta_{1} + 40^\circ = 180^\circ\]

\[\alpha \approx 180^\circ - 40^\circ - 49.132^\circ\]

\[\alpha \approx 90.868^\circ\]

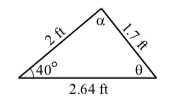
We use the Law of Sines to determine the length $x$ of the side opposite $\alpha$. The resulting triangle is shown on the right.

\[\dfrac{x}{\sin(\alpha)} = \dfrac{1.7}{\sin^(40^\circ)}\]

\[x = \dfrac{1.7\sin(\alpha)}{\sin(40^\circ)}\]

\[x \approx 2.644\space ft\]

$3.15.png$

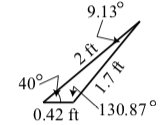
5. Using the same procedure that we did in part (4), we obtain

\[\theta_{2} \approx 130.868^\circ\]

\[\theta_{2} \approx 9.132^\circ\]

\[x_{2} \approx 0.420\space ft\]

The triangle is shown on the right.

$3.15 5.png$

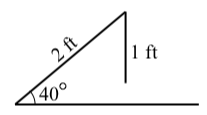
There are times when the Law of Sines will show that there are no triangles that meet certain conditions. We often see this when an equation the Law of Sines produces an equation of the form \[\sin(\theta) = p\]

where $p$ is real number but is not between 0 and 1. For example, changing the conditions in Progress Check 3.15 so that we want a triangle that has a side of length 2 feet that is an adjacent side for an angle of $40^\circ$ and the side opposite the $40^\circ$ angle is to have a length of 1 foot. As in Progress Check 3.15, we let $\theta$ be the angle opposite the side of length 2 feet and use the Law of Sines to obtain

\[\dfrac{\sin(\theta)}{2} = \dfrac{\sin(40^\circ)}{1}\]

\[\sin(\theta) = \dfrac{2\sin(40^\circ)}{1} \approx 1.2856\]

There is no such angle $\theta$ and this shows that there is no triangle that meets the specified conditions. The diagram on the right illustrates the situation.

$p197.png$

Exercise $\PageIndex{3}$

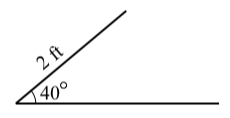
Suppose a triangle has a side of length $2$ feet that is an adjacent side for an angle of $40^\circ$. Is it possible for the side opposite the $40^\circ$ angle to have a length of $3$ feet?

$pc 3.16.png$

Answer

The only difference between this and Progress Check 3.15 is in the length of the side opposite the $40^\circ$ angle. We can use the same diagram. By observation, it appears there is likely only way to draw a side of length $3$ feet. Now we get to the details.

Let $\theta$ be the angle opposite the side of length $2$ feet. Use the Law of Sines to determine $\sin(\theta)$. Use the inverse sine function to determine one solution (rounded to the nearest tenth of a degree) for $\theta$. Call this solution$\theta_{1}$.

This means that there could be two triangles that satisfy the conditions of the problem.

Determine the third angle and the third side when the angle opposite the side of length 2 is $\theta_{1}$. Determine the third angle and the third side when the angle opposite the side of length $2$ is $\theta_{2}$. Now determine the sum $40^\circ + \theta_{2}$ and explain why this is not possible in a triangle.

Let $\theta_{2} = 180^\circ - \theta_{1}$
Explain why (or verify that) $\theta_{2}$ is also a solution of the equation in part (1).

Law of Cosines

We have seen how the Law of Sines can be used to determine information about sides and angles in oblique triangles. However, to use the Law of Since (Equation \ref{lawofsines}) we need to know three pieces of information. We need to know an angle and the length of its opposite side, and in addition, we need to know another angle or the length of another side. If we have three different pieces of information such as the lengths of two sides and the included angle between them or the lengths of the three sides, then we need a different method to determine the other pieces of information about the triangle. This is where the Law of Cosines is useful.

We first explored the Law of Cosines in the beginning activity for this section. Following is the usual formal statement of the Law of Cosines. The proof of the Law of Cosines is included at the end of this section.

Law of Cosines

In a triangle, if $a$, $b$, and $c$ are the lengths of the sides opposite angles $\alpha$, $\beta$, and $\gamma$, respectively, then

\[c^{2} = a^{2} + b^{2} - 2ab\cos(\gamma)\]

\[b^{2} = a^{2} + c^{2} - 2ac\cos(\beta)\]

\[a^{2} = b^{2} + c^{2} - 2bc\cos(\alpha)\]

As with the Law of Sines, there are three equations in the Law of Sines. However, we can remember this with only one equation since the key to using the Law of Cosines is that this law involves 4 quantities. These 4 quantities are the lengths of the three sides and the measure of one of the angles of the triangle as shown in Figure 3.14.

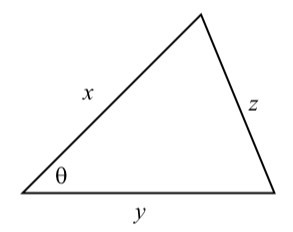
$3.14.png$

Figure $\PageIndex{3}$: Diagram for the Law of Cosines

In this diagram, are the lengths of the three sides and $\theta$ is the angle between the sides $x$ and $y$. Theta can also be thought of as the angle opposite sides. So we can write the Law of Cosines as follows:

Law of Cosines

In a triangle, if $x$, $y$, and $z$ are the lengths of the sides of a triangle and $\theta$ is the angle between the sides $x$ and $y$ as in Figure $\PageIndex{3}$, then

\[z^{2} = x^{2} + y^{2} - 2xy\cos(\theta).\]

The idea is that if you know 3 of these 4 quantities, you can use the Law of Cosines to determine the fourth quantity. The Law of Cosines involves the lengths of all three sides of a triangle and one angle. It states that:

The square of the side opposite an angle is the sum of the squares of the two sides of the angle minus two times the product of the two sides of the angle and the cosine of the angle.

We will explore the use of the Law of Cosines in the next progress check.

Exercise $\PageIndex{4}$

Two sides of a triangle have length $2.5$ meters and $3.5$ meters, and the angle formed by these two sides has a measure of $60^\circ$. Determine the other parts of the triangle.

The first step is to draw a reasonably accurate diagram of the triangle and label the parts. This is shown in the diagram below.

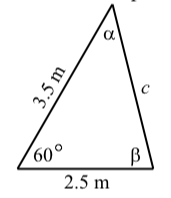
$pc 3.17.png$

Use the Law of Cosines to determine the length of the side opposite the $60^\circ$ angle. ($c$). We now know an angle ($60^\circ$) and the length of its opposite side. We can use the Law of Sines to determine the other two angles. However, remember that we must be careful when using the Law of Sines to determine an angle since the equation may produce two angles.
Use the Law of Sines to determine $\sin(\alpha)$.Determine the two possible values for $\alpha$ and explain why one of them is not possible.
Use the fact that the sum of the angles of a triangle is $180^\circ$ to determine the angle $\beta$.
Use the Law of Sines to check the results.

Answer

1. Using the Law of Cosines, we obtain

\[c^{2} = 3.5^{2} + 2.5^{2} - 2(3.5)(2.5)\cos(60^\circ) = 9.75\]

So $c = \sqrt{9.75} \approx 3.12250\space ft$
2. Using the Law of Sines, we obtain

\[\dfrac{\sin(\alpha)}{2.5} = \dfrac{\sin(60^\circ)}{c}\]

\[\sin(\alpha) = \dfrac{2.5\sin(60^\circ)}{c} \approx 0.69338\] $page385image770554416$

From this, we get $\alpha \approx 43.898^\circ$ or $\alpha \approx 136.102^\circ$. However, since the given angle in $60^\circ$, the second value is not possible since $136.102^\circ + 60^\circ < 180^\circ$. So $\alpha \approx 43.898^\circ$.

Since the sum of the angles of a triangle must be $180^\circ$, we have \[60^\circ + 43.898^\circ + \beta = 180^\circ\] \[\beta \approx 76.102^\circ\]

With the values we have determined, we can check our work by showing that \[\dfrac{\sin(60^\circ)}{c} = \dfrac{\sin(\alpha)}{2.5} = \dfrac{\beta}{3.5} \approx 0.27735.\]

We used the Law of Sines to determine two angles in Progress Check 3.17 and saw that we had to be careful since the equation for the Law of Sines often produces two possible angles. We can avoid this situation by using the Law of Cosines to determine the angles instead. This is because an equation of the form $\cos(\theta) = p$, where p is a real number between $0$ and $1$ has only one solution for $\theta$ between $0^\circ$ and $180^\circ$. The idea is to solve an equation from the Law of Cosines for the cosine of the angle. In Exercise $\PageIndex{4}$, we first determined $\theta^{2} = 3.12250$. We then could have proceeded as follows:

\[2.5^{2} = 3.5^{2} + 3.12250^{2} - 2(3.5)(3.12250)\cos(\alpha)\]
\[2(3.5)(3.12250)\cos(\alpha) = 3.5^{2} + 3.12250^{2} - 2.5^{2}\]
\[\cos(\alpha) = \dfrac{15.75}{21.8575} \approx 0.720577\]

We can then use the inverse cosine function and obtain $\alpha \approx 43.898^\circ$, which is what we obtained in Exercise $\PageIndex{4}$.

We can now use the fact that the sum of the angles in a triangle is $180^\circ$ to determine $\beta$ but for completeness, we could also use the Law of Cosines to determine $\beta$ and then use the angle sum for the triangle as a check on our work.

Exercise $\PageIndex{5}$

The three sides of a triangle have lengths of $3$ feet, $5$ feet, and $6$ feet. Use the Law of Cosines to determine each of the three angles.

Answer

The first step is to draw a reasonably accurate diagram and label the angles. We will use the diagram on the right.

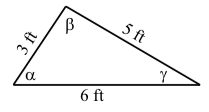
$3.18.png$

Law of Cosines, we obtain

\[5^{2} = 3^{2} + 6^{2} - 2(3)(6)\cos(\alpha)\] \[\cos(\alpha) = \dfrac{20}{36}\] \[\alpha \approx 56.251^\circ\]

\[6^{2}\ = 3^{2} + 5^{2} - 2(3)(5)\cos(\beta)\] \[\cos(\beta) = \dfrac{-2}{30}\] \[\beta \approx 98.823^\circ\]

\[3^{2}\ = 5^{2} + 6^{2} - 2(5)(6)\cos(\gamma)\] \[\cos(\gamma) = \dfrac{52}{60}\] \[\gamma \approx 29.926^\circ\]

We check these results by verifying that $\alpha + \beta + \gamma = 180^\circ$.

Appendix – Proof of the Law of Sines

We will use what we know about right triangles to prove the Law of Sines. The key idea is to create right triangles from the diagram for a general triangle by drawing an altitude of length $h$ from one of the vertices. We first note that if $\alpha$, $\beta$, and $\gamma$ are the three angles of a triangle, then \[\alpha + \beta + \gamma = 180^\circ\]

This means that at most one of the three angles can be an obtuse angle (between $90^\circ$ and $180^\circ$), and hence, at least two of the angles must be acute (less than $90^\circ$).Figure 3.15 shows the two possible cases for a general triangle. The triangle on the left has three acute angles and the triangle on the right has two acute angles ($\alpha$ and $\beta$) and and one obtuse angle $\gamma$.

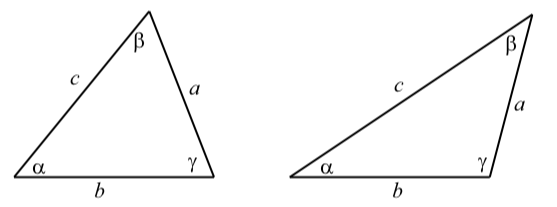
$3.15.png$

Figure $\PageIndex{4}$: General Triangles

We will now prove the Law of Sines for the case where all three angles of the triangle are acute angles. The proof for the case where one angle of the triangle is obtuse is included in the exercises. The key idea is to create right triangles from the diagram for a general triangle by drawing altitudes in the triangle as shown in Figure $\PageIndex{5}$ where an altitude of length $h$ is drawn from the vertex of angle $\beta$ and an altitude of length $k$ is drawn from the vertex of angle $\gamma$

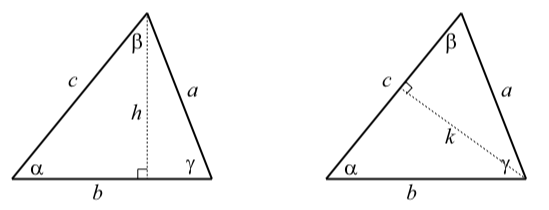
$3.16.png$

Figure $\PageIndex{5}$: Diagram for the Proof of the Law of Sines

Using the right triangles in the diagram on the left, we see that \[\sin(\alpha) = \dfrac{h}{c}\]\[\sin(\gamma) = \dfrac{h}{a}\]

From this, we can conclude that \[h = c\sin(\alpha)\]\[h = a\sin(\gamma)\]

Using the two equations in (1), we can use the fact that both of the right sides are equal to h to conclude that \[c\sin(\alpha) = a\sin(\gamma)\]
Now, dividing both sides of the last equation by $ac$, we see that

\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\gamma)}{c}\]

We now use a similar argument using the triangle on the right in Figure $\PageIndex{5}$. We see that \[\sin(\alpha) = \dfrac{k}{b}\]\[\sin(\beta) = \dfrac{k}{a}\]

From this, we obtain \[k = b\sin(\alpha)\]\[k = a\sin(\beta)\]and so \[b\sin(\alpha) = a\sin(\beta)\]\[\dfrac{\sin(\alpha)}{a} = \dfrac{\sin(\beta)}{b}\]

We can now use equations (2) and (3) to complete the proof of the Law of Sines,

which is \[\dfrac{\sin(\alpha)}{a} = = \dfrac{\sin(\beta)}{b} = \dfrac{\sin(\gamma)}{c}.\]

Appendix – Proof of the Law of Cosines

As with the Law of Sines, we will use results about right triangles to prove the Law of Cosines. We will also use the distance formula. We will start with a general triangle with $a$, $b$, and $c$ representing the lengths of the sides opposite the angles $\alpha$, $\beta$, and $\gamma$, respectively. We will place the angle $\gamma$ in standard position in the coordinate system as shown in Figure $\PageIndex{6}$.

In this diagram, the angle $\gamma$ is shown as an obtuse angle but the proof would be the same if $\gamma$ was an acute angle. We have labeled the vertex of angle $\alpha$ as $A$ with coordinates $(x, y)$ and we have drawn a line from $A$ perpendicular to the $x$-axis. So from the definitions of the trigonometric functions in Section 3.1, we see that

\[\cos(\gamma) = \dfrac{x}{b}\]\[x = b\cos(\gamma)\]

\[\sin(\gamma) = \dfrac{y}{b}\]\[y = b\sin(\gamma)\]

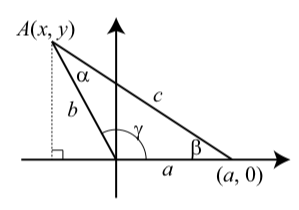
$3.17.png$
Figure $\PageIndex{6}$: Diagram for the Law of Cosines

We now use the distance formula with the points $A$ and the vertex of angle $\beta$, which has coordinates $(a, 0)$. This gives

\[c = \sqrt{(x - a)^{2} + (y - 0)^{2}}\]
\[c^{2} = (x - a)^{2} + y^{2}\]
\[c^{2} = x^{2} - 2ax + a^{2}+ y^{2}\]

We now substitute the values for $x$ and $y$ in equation (4) and obtain

\[c^{2} = b^{2}\cos^{2}(\gamma) - 2ab\cos(\gamma) + a^{2} + b^{2}sin^{2}(\gamma)\]
\[c^{2} = a^{2} + b^{2}\cos^{2}(\gamma) + b^{2}sin^{2}(\gamma) - 2ab\cos(\gamma)\]
\[c^{2} = a^{2} + b^{2}(\cos^{2}(\gamma) + sin^{2}(\gamma)) - 2ab\cos(\gamma)\]

We can now use the last equation and the fact that $cos^{2}(\gamma) + \sin^{2}(\gamma) = 1$ to conclude that

\[c^{2} = a^{2} + b^{2} -2ab\cos(\gamma)\]

This proves one of the equations in the Law of Cosines. The other two equations can be proved in the same manner by placing each of the other two angles in standard position.

Summary

In this section, we studied the following important concepts and ideas:

The Law of Sines and the Law of Cosines can be used to determine the lengths of sides of a triangle and the measure of the angles of a triangle.

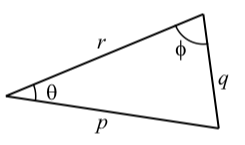
$summary.png$

The Law of Sines states that if q is the length of the side opposite the angle $\theta$ and $p$ is the length of the side opposite the angle $\theta$, then \[\dfrac{\sin(\theta)}{q} = \dfrac{\sin(\phi)}{p}\]

The Law of Cosines states that if $p$, $q$, and $r$ are the lengths of the sides of a triangle and $\theta$ is the angles opposite the side $q$, then

\[q^{2} = p^{2} + r^{2} - 2pr\cos(\theta).\]

Each of the equations in the Law of Sines and the Law of Cosines involves four variables. So if we know the values of three of the variables, then we can use the appropriate equation to solve for the fourth variable.