3.5: Vectors from a Geometric Point of View

Last updated
Save as PDF

Page ID: 7115

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Focus Questions

The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.

What is a vector?
How do we use the geometric form of vectors to find the sum of two vectors?
How do we use the geometric form of vectors to find a scalar multiple of a vector?
How do we use the geometric form of vectors to find the difference of two vectors?
What is the angle between two vectors?
Why is force a vector and how do we use vectors and triangles to determine forces acting on an object?

We have all had the experience of dropping something and watching it fall to the ground. What is happening, of course, is that the force of gravity is causing the object to fall to the ground. In fact, we experience the force of gravity everyday simply by being on Earth. Each person’s weight is a measure of the force of gravity since pounds are a unit of force. So when a person weighs 150 pounds, it means that gravity is exerting a force of 150 pounds straight down on that person. Notice that we described this with a quantity and a direction (straight down). Such a quantity (with magnitude and direction) is called a vector.

Now suppose that person who weighs 150 pounds is standing on a hill. In mathematics, we simplify the situation and say that the person is standing on an inclined plane as shown in Figure 3.20. (By making the hill a straight line, we simplify the mathematics involved.) The diagram in Figure $\PageIndex{1}$, an object is on the inclined plane at the point $P$. The inclined plane makes an angle of $\theta$ with the horizontal. The vector $\textbf{w}$ shows the weight of the object (force of gravity, straight down). The diagram also shows two other vectors. The vector $\textbf{b}$ is perpendicular

$3.20.png$

Figure $\PageIndex{1}$: Inclined Plane

to the plane represents the force that the object exerts on the plane. The vector $\textbf{a}$ is perpendicular to $\textbf{b}$ and parallel to the inclined plane. This vector represents the force of gravity along the plane. In this and the next section, we will learn more about these vectors and how to determine the magnitudes of these vectors. We will also see that with our definition of the addition of two vectors that $\textbf{w} = \textbf{a} + \textbf{b}$.

Definitions

There are some quantities that require only a number to describe them. We call this number the magnitude of the quantity. One such example is temperature since we describe this with only a number such as 68 degrees Fahrenheit. Other such quantities are length, area, and mass. These types of quantities are often called scalar quantities. However, there are other quantities that require both a magnitude and a direction. One such example is force, and another is velocity. We would describe a velocity with something like 45 miles per hour northwest. Velocity and force are examples of a vector quantity. Other examples of vectors are acceleration and displacement.

Some vectors are closely associated with scalars. In mathematics and science, we make a distinction between speed and velocity. Speed is a scalar and we would say something like our speed is 65 miles per hour. However, if we used a velocity, we would say something like 65 miles per hour east. This is different than a velocity of $65$ miles per hour north even though in both cases, the speed is 65 miles per hour.

Definitions: Vectors and Scalars

A vector is a quantity that has both magnitude and direction.
A scalar is a quantity that has magnitude only.

Geometric Representation of Vectors

Vectors can be represented geometrically by arrows (directed line segments). The arrowhead indicates the direction of the vector, and the length of the arrow describes the magnitude of the vector.

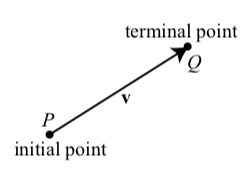
$GRV.png$

A vector with initial point $P$ (the tail of the arrow) and terminal point $Q$ (the tip of the arrowhead) can be represented by

\[\overrightarrow{PQ}, \textbf{v}, or \overrightarrow{v}.\]

We often write $v = \overrightarrow{PQ}$. In this text, we will use boldface font to designate a vector. When writing with pencil and paper, we always use an arrow above the letter (such as $\overrightarrow{v}$) to designate a vector. The magnitude (or norm or length) of the vector $\textbf{v}$ is designated by $\textbf{|v|}$. It is important to remember that $|\textbf{v}|$ is a number that represents the magnitude or length of the vector $\textbf{v}$.

According to our definition, a vector possesses the attributes of length (magnitude) and direction, but position is not mentioned. So we will consider two vectors to be equal if they have the same magnitude and direction. For example, if two different cars are both traveling at $45$ miles per hour northwest (but in different locations), they have equal velocity vectors. We make a more formal definition.

Definition: Equal Vectors

Two vectors are equal if and only if they have the same magnitude and the same direction. When the vectors $\textbf{v}$ and $\textbf{w}$ are equal, we write $\textbf{v} = \textbf{v}$.

Exercise $\PageIndex{1}$

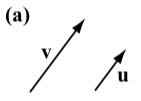
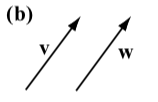
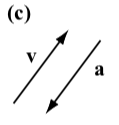
The following diagrams show the vector $\textbf{v}$ next to four other vectors. Which (if any) of these four vectors are equal to the vector $\textbf{v}$?

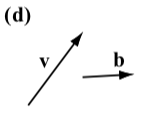
$pc3.24 a.png$ $pc3.24 b.png$ $pc3.24 c.png$ $pc3.24 d.png$

Answer: The vector $\textbf{w}$ is the only vector that is equal to the vector $\textbf{v}$. Vector $\textbf{u}$ has the same direction as $\textbf{v}$ but a different magnitude. Vector $\textbf{a}$ has the same magnitude as $\textbf{v}$ but a different direction (note that the direction of a is the opposite direction of $\textbf{v}$). Vector $\textbf{b}$ has a different direction and a different magnitude than $\textbf{v}$.

Operations on Vectors

Scalar Multiple of a Vector

Doubling a scalar quantity is simply a matter of multiplying its magnitude by $2$. For example, if a container has $20$ ounces of water and the amount of water is doubled, it will then have $40$ ounces of water. What do we mean by doubling a vector? The basic idea is to keep the same direction and multiply the magnitude by $2$. So if an object has a velocity of $5$ feet per second southeast and a second object has a velocity of twice that, the second object will have a velocity of $10$ feet per second in the southeast direction. In this case, we say that we multiplied the vector by the scalar $2$. We now make a definition that also takes into account that a scalar can be negative.

Definition

For any vector $\textbf{v}$ and any scalar $c$, the vector $c\textbf{v}$ (called a scalar multiple of the vector $\textbf{v}$ is a vector whose magnitude is $|c|$ times the magnitude of the vector $\textbf{v}$.

If $c > 0$, then the direction of $c\textbf{v}$ is the same as the direction of $\textbf{v}$.
If $c < 0$, then the direction of $c\textbf{v}$ is the opposite of the direction of $\textbf{v}$.
If $c = 0$, then $c\textbf{v} = 0 \textbf{v} = 0$.

The vector $\textbf{0}$ is called the zero vector and the zero vector has no magnitude and no direction. We sometimes write $\overrightarrow{0}$ for the zero vector.

In this definition, $|c|$ is the absolute value of the scalar $c$. Care must be taken not to confuse this with the notation $\textbf{|v|}$, which is the magnitude of the vector $\textbf{v}$. This is one reason it is important to have a notation that clearly indicates when we are working with a vector or a scalar.

Addition of Vectors

We illustrate how to add vectors with two displacement vectors. As with velocity and speed, there is a distinction between displacement and distance. Distance is a scalar. So we might say that we have traveled 2 miles. Displacement, on the other hand, is a vector consisting of a distance and a direction. So the vectors 2 miles north and 2 miles east are different displacement vectors.

Now if we travel 3 miles north and then travel 2 miles east, we end at a point that defines a new displacement vector. See the diagram to the right. In this diagram, $\textbf{u}$ is “3 miles north” and $\textbf{v}$ is “2 miles east.” The vector sum $\textbf{u} + \textbf{v}$ goes from the initial point of $\textbf{u}$ to the terminal point of $\textbf{v}$.

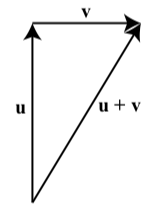
$Addition of v.png$

Definition: sum of two vectors

The sum of two vectors is defined as follows: We position the vectors so that the initial point of $\textbf{w}$ coincides with the terminal point of $\textbf{v}$. The vector $\textbf{v} + \textbf{w}$ is the vector whose initial point coincides with the initial point of $\textbf{v}$ and whose terminal point coincides with the terminal point of $\textbf{w}$.

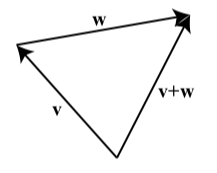
$def.png$

The vector $\textbf{v} + \textbf{w}$ is called the sum or resultant of the vectors $\textbf{v}$ and $\textbf{w}$.

In the definition, notice that the vectors $\textbf{v}$, $\textbf{w}$, and $\textbf{v} + \textbf{w}$ are placed so that the result is a triangle. The lengths of the sides of that triangle are the magnitudes of these sides $|\textbf{v}|$, $|\textbf{w}|$, and $|\textbf{v} + \textbf{w}|$. If we place the two vectors $\textbf{v}$ and $\textbf{w}$ so that their initial points coincide, we can use a parallelogram to add the two vectors. This is shown in Figure $\PageIndex{2}$.

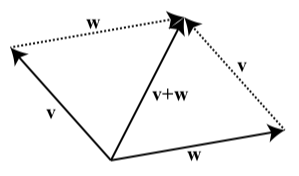
$3.21.png$

Figure $\PageIndex{2}$: Sum of Two Vectors Using a Parallelogram

Notice that the vector $\textbf{v}$ forms a pair of opposite sides of the parallelogram as does the vector $\textbf{w}$.

Exercise $\PageIndex{2}$

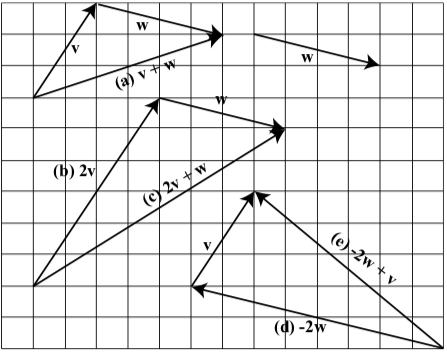
The following diagram shows two vectors, $\textbf{v}$ and $\textbf{w}$. Draw the following vectors:

$\textbf{v} + \textbf{w}$
$2\textbf{v}$
$2\textbf{v} + \textbf{w}$
$-2\textbf{w}$
$-2\textbf{w + v}$

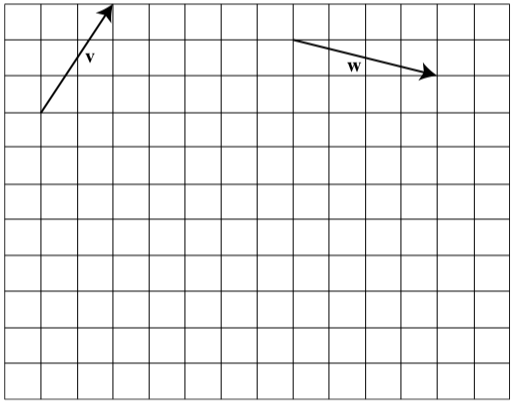
$pc 3.25.png$

Answer: $3.25.png$

Subtraction of Vectors

Before explaining how to subtract vectors, we will first explain what is meant by the “negative of a vector.” This works similarly to the negative of a real number. For example, we know that when we add $-3$ to $3$, the result is $0$. That is, $3 + (-3) = 0$

We want something similar for vectors. For a vector $\textbf{w}$, the idea is to use the scalar multiple $(-1)\textbf{w}$. The vector $(-1)\textbf{w}$ has the same magnitude as $\textbf{w}$ but has the opposite direction of $\textbf{w}$. We define $-\textbf{w}$ to be $(-1)\textbf{w}$. Figure shows that when we add $-\textbf{w}$ to $\textbf{w}$, the terminal point of the sum is the same as the initial point of the sum and so the result is the zero vector. That is, $\textbf{w} + (-\textbf{w}) = \textbf{0}$.

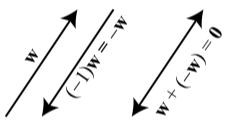
$3.22.png$

Figure $\PageIndex{3}$: The Sum of a Vector and Its Negative

We are now in a position to define subtraction of vectors. The idea is much the same as subtraction of real numbers in that for any two real numbers $a$ and $b$, $a - b = a + (-b)$.

Definition: Difference between vectors

For any two vectors $\textbf{v}$ and $\textbf{w}$, the difference between $\textbf{v}$ and $\textbf{w}$ is denoted by $\textbf{v} - \textbf{w}$ and is defined as follows:

\[\textbf{v} - \textbf{w} = \textbf{v} + (-\textbf{w}).\]

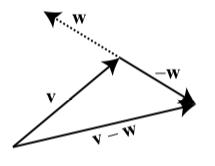
$def2.png$

We also say that we are subtracting the vector $\textbf{w}$ from the vector $\textbf{v}$.

Exercise $\PageIndex{3}$

The following diagram shows two vectors, $\textbf{v}$ and $\textbf{w}$. Draw the following vectors:

$-\textbf{w}$
$\textbf{v - w}$
$-\textbf{v}$
$\textbf{w - v}$

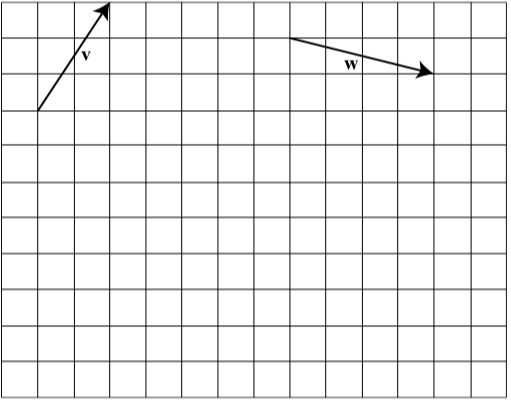
$pc 3.26.png$

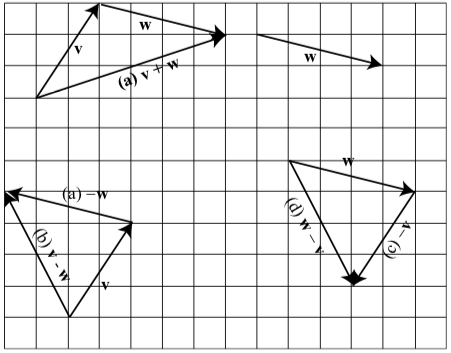
Answer: $3.26.png$

The Angle Between Two Vectors

We have seen that we can use triangles to help us add or subtract two vectors. The lengths of the sides of the triangle are the magnitudes of certain vectors. Since we are dealing with triangles, we will also use angles determined by the vectors.

Definition

The angle $\theta$ between vectors is the angle formed by these two vectors (with $0^\circ \leq \theta \leq 180^\circ$) when they have the same initial point.

So in the diagram on the left in Figure $\PageIndex{4}$, the angle $\theta$ is the angle between the vectors $\textbf{v}$ and $\textbf{w}$. However, when we want to determine the sum of two angles, we often form the parallelogram determined by the two vectors as shown in the diagram on the right in Figure $\PageIndex{3}$. (See page 422 in Appendix C for a summary of properties of a parallelogram.) We then will use the angle $180^\circ - \theta$ and the Law of Cosines since we the two sides of the triangle are the lengths of $\textbf{v}$ and $\textbf{w}$ and the included angle is $180^\circ - \theta$. We will explore this in the next progress check.

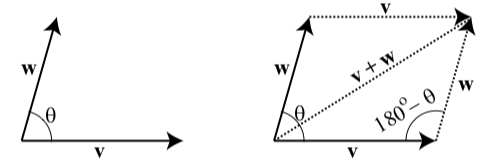
$3.23.png$

Figure $\PageIndex{3}$: Angle Between Two Vectors

Exercise $\PageIndex{4}$

Suppose that the vectors $\textbf{a}$ and $\textbf{b}$ have magnitudes of 80 and 60, respectively, and that the angle $\theta$ between the two vectors is 53 degrees. In Figure 3.24, we have drawn the parallelogram determined by these two vectors and have labeled the vertices for reference.

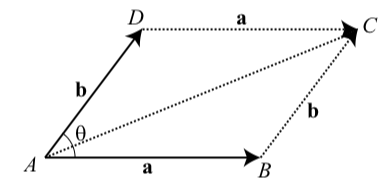
$3.24.png$
Figure 3.24: Diagram for Progress Check 3.27

Remember that a vector is determined by its magnitude and direction. We will determine $|\textbf{a + b}|$ and the measure of the angle between $\textbf{a}$ and $\textbf{a + b}$

Determine the measure of $\angle ABC$.

In $\triangle ABC$, the length of side $AB$ is $|\textbf{a}| = 80$ and the length of side $BC$ is $|\textbf{b}| = 60$. Use this triangle and the Law of Cosines to determine the length of the third side, which is $|\textbf{a + b}|$.

Determine the measure of the angle between $\textbf{a}$ and $\textbf{a + b}$. This is $\angle CAB$ in $\triangle ABC$.

Answer

1. $\angle{ABC} = 180^\circ - \theta = 127^\circ$.

2. Using the Law of Cosines, we see that

\[|\textbf{a} + \textbf{a}|^{2} = |\textbf{a}|^{2} + |\textbf{b}|^{2} - 2|\textbf{a}|\cdot |\textbf{b}|\cos(\angle{ABC}) = 80^{2} + 60^{2} -2\cdot 60 \cdot 80 \cos(127^\circ) = 10000 - 9600\cos(127^\circ) \approx 15777.42422\] so we see that $|\textbf{a} + \textbf{b} \approx 125.61|.$

3. The angle between the vectors a and a C b is †CAB. In 4ABC , we know that †ABC D 127ı, and so †CAB must be an acute angle. We will use the Law of Sines to determine this angle.

\[\dfrac{\sin(\angle{CAB})}{|\textbf{b}|} = \dfrac{\sin(\angle{CAB})}{|\textbf{a} + \textbf{b}|}\]
\[\sin(\angle{CAB} = \dfrac{60\sin(127^\circ)}{|\textbf{a} + \textbf{b}|}\]
\[\sin(\angle{CAB} \approx 0.38148341\]
So the angle between the vectors $\textbf{a}$ and $\textbf{a} + \textbf{b}$ is approximately $22.43^\circ$.

Force

An important vector quantity is that of force. In physics, a force on an object is defined as any interaction that, when left unopposed, will change the motion of the object. So a force will cause an object to change its velocity, that is the object will accelerate. More informally, a force is a push or a pull on an object.

One force that affects our lives is the force of gravity. The magnitude of the force of gravity on a person is that person’s weight. The direction of the force of gravity is straight down. So if a person who weighs 150 pounds is standing still on the ground, then the ground is also exerting a force of 150 pounds on the person in the upward direction. The net force on the stationary person is zero. This is an example of what is known as static equilibrium. When an object is in static equilibrium, the sum of the forces acting on the object is equal to the zero vector.

Example $\PageIndex{1}$: Object Suspended from a Ceiling

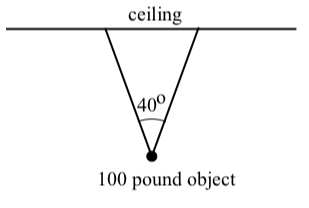
$example 3.28.png$

Suppose a 100 pound object is suspended from the ceiling by two wires that form a $40^\circ$ angle as shown in the diagram to the right. Because the object is stationary, the two wires must exert a force on the object so that the sum of these two forces is equal to 100 pounds straight up. (The force of gravity is 100 pounds straight down.)

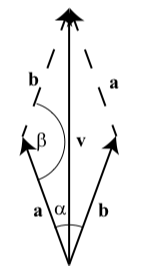
$example 3.28 2.png$

We will assume that the two wires exert an forces of equal magnitudes and that the angle between these forces and the vertical in $20^\circ$. So our first step is to draw a picture of these forces, which is shown on the right. The vector $\textbf{v}$ is a vector of magnitude 100 pounds. The vectors $\textbf{a}$ and $\textbf{b}$ are the vectors for the forces exerted by the two wires. (We have $|\textbf{a}| = |\textbf{b}|$.) We also know that $\alpha = 20^\circ$ and so by the properties of parallelograms, $\beta = 140^\circ$.

Exercise $\PageIndex{5}$

Use triangle trigonometry to determine the magnitude of the vector $\textbf{a}$ in Example 3.28. Note that we already know the direction of this vector.

Answer

Using the Law of Sines, we see that

\[\dfrac{|\textbf{a}|}{\sin(20^\circ)} = \dfrac{100}{\sin(140^\circ)}\]
\[|\textbf{a}| = \dfrac{100\sin(20^\circ)}{\sin(140^\circ)}\]
\[|\textbf{a}| \approx 53.21\]
The magnitude of the vector a (and the vector b) is approximately $53.21$ pounds.

Inclined Planes

At the beginning of this section, we discussed the forces involved when an object is place on an inclined plane. Figure 3.25 is the diagram we used, but we now have added labels for some of the angles. Recall that the vector $\textbf{w}$ shows the weight of the object (force of gravity, straight down), the vector $\textbf{b}$ is perpendicular to the plane and represents the force that the object exerts on the plane, and the vector $\textbf{a}$ is perpendicular to $\textbf{b}$ and parallel to the inclined plane. This vector represents the force of gravity along the plane. Notice that we have also added a second copy of the vector a that begins at the tip of the vector $\textbf{b}$.

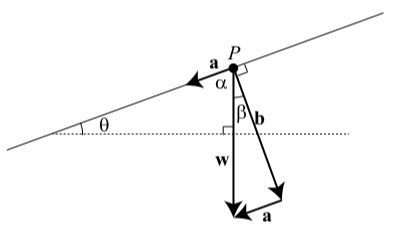
$3.25.png$

Figure 3.25: Inclined Plane

Using the angles shown, we see that $\alpha + \beta = 90^\circ$ since they combine to form a right angle, and $\alpha + \theta = 90^\circ$ since they are the two acute angles in a right triangle. From this, we conclude that $\beta = \theta$. This gives us the final version of the diagram of the forces on an inclined plane shown in Figure 3.26. Notice that the vectors $\textbf{a}$,

$3.26.png$

Figure 3.26: Inclined Plane

$\textbf{b}$, and $\textbf{w}$ form a right triangle, and so we can use right triangle trigonometry for problems dealing with the forces on an inclined plane.

Exercise $\PageIndex{6}$

An object that weighs $250$ pounds is placed on an inclined plane that makes an angle of $12^\circ$ degrees with the horizontal. Using a diagram like the one in Figure 3.26, determine the magnitude of the force against the plane caused by the object and the magnitude of the force down the plane on the object due to gravity.

Note: The magnitude of the force down the plane will be the force in the direction up the plane that is required to keep the object stationary.

Answer

Using the notation in Figure 3.26, we obtain the following:

\[\dfrac{|\textbf{b}|}{|\textbf{w}|} = \cos(12^\circ)\]
\[\dfrac{|\textbf{a}|}{|\textbf{w}|} = \sin(12^\circ)\]
\[|\textbf{b}| = |\textbf{w}|\cos(12^\circ)\]
\[|\textbf{a}| = |\textbf{w}|\sin(12^\circ)\]
\[|\textbf{b}| \approx 244.54\]
\[|\textbf{a}| \approx 51.98\] $page390image792885200$

The object exerts a force of about $244.54$ pounds perpendicular to the plane and the force of gravity down the plane on the object is about $51.98$ pounds. So in order to keep the object stationary, a force of about $51.98$ pounds up the plane must be applied to the object.

Summary

In this section, we studied the following important concepts and ideas:

Vectors and Scalars
- A vector is a quantity that has both magnitude and direction.
- A scalar is a quantity that has magnitude only.
- Two vectors are equal if and only if they have the same magnitude and the same direction.
Scalar Multiple of a Vector

If $c > 0$, then the direction of $c\textbf{v}$ is the same as the direction of $\textbf{v}$.
If $c < 0$, then the direction of $c\textbf{v}$ is the opposite of the direction of $\textbf{v}$.
If $c = 0$, then $c\textbf{v} = 0\textbf{v} = 0$.

The vector $\(\textbf{0}$\) is called the zero vector and the zero vector has no magnitude and no direction. We sometimes write $\overrightarrow{0}$ for the zero vector.

The Sum of Two Vectors

$def.png$

The vector $\textbf{v} + \textbf{w}$ is called the sum or resultant of the vectors $\textbf{v}$ and $\textbf{w}$.

The Angle Between Two Vectors

The angle $\theta$ between vectors is the angle formed by these two vectors (with $0^\circ \leq \theta \leq 180^\circ$) when they have the same initial point.