4.5: Sum-Product Identities

Focus Questions

The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.

• What are the Product-to-Sum Identities for the sine and cosine?
• What are the Sum-to-Product Identities for the sine and cosine?
• Why are these identities useful?

In general, trigonometric equations are very difficult to solve exactly. We have been using identities to solve trigonometric equations, but there are still many more for which we cannot find exact solutions. Consider, for example, the equation

\[\sin(3x) + \sin(x) = 0\]

The graph of \(y = \sin(3x) + \sin(x)\) is shown in Figure \(\PageIndex{1}\). We can see that there are many solutions, but the identities we have so far do not help us with this equation. What would make this equation easier to solve is if we could rewrite the sum on the left as a product – then we could use the fact that a product is zero if and only if one of its factors is 0. We will later introduce the Sum-to-Product Identities that will help us solve this equation.

Beginning Activity

Let \(A = 30^\circ\) and \(B = 45^\circ\). Calculate

\[\cos(A)\cos(B)\space and \space (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

What do you notice?

Product-to-Sum Identities

The Cosine Sum and Difference Identities

\[\cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]

\[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]

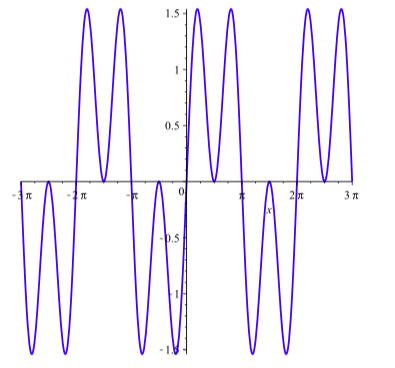
Figure \(\PageIndex{1}\): Graph of \(y = \sin(3x) + \sin(x)\).

will allow us to develop identities that will express product of cosines or sines in terms of sums of cosines and sines. To see how these identities arise, we add the left and right sides of (4) and (5) to obtain

\[\cos(A - B) + \cos(A + B) = 2\cos(A)\cos(B)\]

So

\[\cos(A)\cos(B) = (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

Similarly, subtracting the left and right sides of (5) from (4) gives us

\[\cos(A - B) - \cos(A + B) = 2\sin(A)\cos(B)\]

So

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A + B)]\]

We can similarly obtain a formula for \(\cos(A)\cos(B)\). In this case we use the sine sum and difference formulas

\[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\]

\[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]

Adding the left and right hand sides of (6) and (7) yields

\[\sin(A - B) + \sin(A + B) = 2\sin(A)\cos(B)\]

So

\[\sin(A)\cos(B) = (\dfrac{1}{2})[\sin(A + B) + \sin(A - B)]\]

Product-to-Sum Identities

For any numbers \(A\) and \(B\) we have

\[\cos(A)\cos(B) = (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A + B)]\]

\[\sin(A)\cos(B) = (\dfrac{1}{2})[\sin(A + B) + \sin(A - B)]\]

Exercise \(\PageIndex{1}\)

Find the exact value of \(\sin(52.5^\circ)\sin(7.5^\circ)\).

Answer

To determine the exact value of \(\sin(52.5^\circ)\sin(7.5^\circ)\), we will use the Product-to- Sum identity

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A + B)]\]

So we see that
\[\sin(52.5^\circ)\sin(7.5^\circ) = (\dfrac{1}{2})[\cos(45^\circ) - \cos(60^\circ)] = (\dfrac{1}{2})[\dfrac{\sqrt{2}}{2} - \dfrac{1}{2}] = \dfrac{\sqrt{2} - 1}{4}\]

Sum-to-Product Identities

As our final identities, we derive the reverse of the Product-to-Sum identities. These identities are called the Sum-to-Product identities. For example, to verify the identity

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

we first note that \(A = \dfrac{A + B }{2}\) and \(B = \dfrac{A + B}{2} - \dfrac{A - B}{2}\). So

\[\cos(A) = \cos(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) - \sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]
and

\[\cos(B) = \cos(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) + \sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Adding the left and right sides of (8) and (9) results in

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

Also, if we subtract the left and right hands sides of (9) from (8) we obtain

\[\cos(A) - \cos(B) = -2\sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Similarly,

\[\sin(A) = \sin(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) + \cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]
and

\[\sin(B) = \sin(\dfrac{A + B}{2} + \dfrac{A - B}{2}) = \sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2}) - \cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Adding the left and right sides of (10) and (11) results in

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

Again, if we subtract the left and right hands sides of (11) from (10) we obtain

\[\sin(A) - \sin(B) = 2\cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Sum-to-Product Identities

For any numbers \(A\) and \(B\) we have

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\cos(A) - \cos(B) = -2\sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\sin(A) - \sin(B) = 2\cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

Exercise \(\PageIndex{2}\)

Find the exact value of \(\cos(112.5^\circ) + \cos(67.5^\circ)\).

Answer

To determine the exact value of \(\cos(112.5^\circ) + \cos(67.5^\circ)\), we will use the Sum-to-Product Identity

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

So we see that

\[\cos(112.5^\circ) + \cos(67.5^\circ) = 2\cos(\dfrac{180^\circ}{2})\cos(\dfrac{45^\circ}{2}) = \cos(90^\circ)\cos(22.5^\circ) = 0\cdot\cos(22.5^\circ) = 0\]

We can use these Sum-to-Product and Product-to-Sum Identities to solve even more types of trigonometric equations.

Example \(\PageIndex{1}\): (Solving Equations Using the Sum-to-Product Identity)

Let us return to the problem stated at the beginning of this section to solve the equation

\[\sin(3x) + \sin(x) = 0\]

Using the Sum-to-Product

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

we can rewrite the equation as follows:

\[\sin(3x) + \sin(x) = 0\]

\[2\sin(\dfrac{4x}{2})\cos(\dfrac{x}{2}) = 0\]

\[2\sin(2x)\cos(\dfrac{x}{2}) = 0\]

The advantage of this form is that we now have a product of functions equal to \(0\), and the only way a product can equal \(0\) is if one of the factors is \(0\). This reduces our original problem to two equations we can solve:

\[\sin(2x) = 0\] or \[\cos(\dfrac{x}{2}) = 0\]

We know that \(\sin(2x) = 0\) when \(2x = k\pi\) or \(x = k\dfrac{\pi}{2}\), where \(k\) is any integer, and \(\cos(\dfrac{x}{2}) = 0\) when \(\dfrac{x}{2} = \dfrac{\pi}{2} + k\pi\) or \(x = \pi + k2\pi\), where \(k\) is any integer. These solutions can be seen where the graph of \(y = \sin(3x) + \sin(x)\) intersects the \(x\)-axis as illustrated in Figure \(\PageIndex{2}\).

Summary of Trigonometric Identities

Trigonometric identities are useful in that they allow us to determine exact values for the trigonometric functions at more points than before and also provide tools for deriving new identities and for solving trigonometric equations. Here we provide a summary of our trigonometric identities.

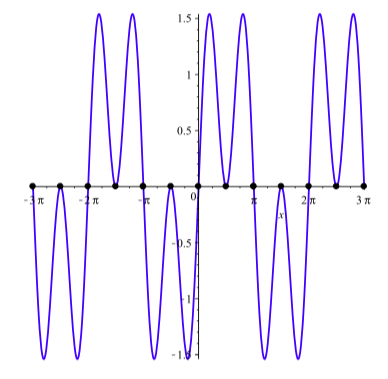
Figure \(\PageIndex{2}\): Graph of \(y = \sin(3x) + \sin(x)\).

Cofunction Identities

\[\cos(\dfrac{\pi}{2} - A) = \sin(A)\]
\[\sin(\dfrac{\pi}{2} - A) = \cos(A)\]
\[\tan(\dfrac{\pi}{2} - A) = \cot(A)\]

Half Angle Identities

\[\cos^{2}(\dfrac{A}{2}) = \dfrac{1 + \cos(A)}{2}\]
\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]
\[\sin^{2}(\dfrac{A}{2}) = \dfrac{1 - \cos(A)}{2}\]
\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]
\[\tan(\dfrac{A}{2}) = \sqrt{\dfrac{\sin(A)}{1 + \cos(A)}}\]
\[\tan(\dfrac{A}{2}) = \sqrt{\dfrac{1 - \cos(A)}{\sin(A)}}\]

The signs of \(\cos(\dfrac{A}{2}\) and \(\sin(\dfrac{A}{2}\) depend on the quadrant in which \(\dfrac{A}{2}\) lies.

Double Angle Identities

\[\sin(2A) = 2\cos(A)\sin(A)\]
\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]
\[\cos(2A) = 1 - 2\sin^{2}(A)\]
\[\cos(2A) = 2\cos^{2}(A) - 1\]
\[\tan(2A) = \dfrac{2\tan(A)}{1 - \tan^{2}(A)}\]

Cosine Difference and Sum Identities

\[\cos(A) - \cos(B) = \cos(A)\cos(B) + \sin(A)\sin(B)\]

\[\cos(A) + \cos(B) = \cos(A)\cos(B) - \sin(A)\sin(B)\]

Sine Difference and Sum Identities

\[\sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B)\]

\[\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)\]

Tangent Difference and Sum Identities

\[\tan(A - B) = \dfrac{\tan(A) - \tan(B)}{1 + \tan(A)\tan(B)}\]
\[\tan(A + B) = \dfrac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)}\]

Product-to-Sum Identities

\[\cos(A)\cos(B) = (\dfrac{1}{2})[\cos(A + B) + \cos(A - B)]\]

\[\sin(A)\sin(B) = (\dfrac{1}{2})[\cos(A - B) - \cos(A - B)]\]

\[\sin(A)\cos(B) = (\dfrac{1}{2})[\sin(A + B) + \sin(A - B)]\]

Sum-to-Product Identities

\[\cos(A) + \cos(B) = 2\cos(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\cos(A) - \cos(B) = -2\sin(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]

\[\sin(A) + \sin(B) = 2\sin(\dfrac{A + B}{2})\cos(\dfrac{A - B}{2})\]

\[\sin(A) - \sin(B) = 2\cos(\dfrac{A + B}{2})\sin(\dfrac{A - B}{2})\]