5.1: The Complex Number System
- Page ID
- 7124
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- What is a complex number?
- What does it mean for two complex numbers to be equal?
- How do we add two complex numbers together?
- How do we multiply two complex numbers together?
- What is the conjugate of a complex number?
- What is the modulus of a complex number?
- How are the conjugate and modulus of a complex number related?
- How do we divide one complex number by another?
The quadratic formula \(x = \dfrac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\) allows us to find solutions to the quadratic equation \(ax^2+ bx + c = 0\). For example, the solutions to the equation \(x^{2} + x + 1 = 0\) are
\[x = \dfrac{-1 \pm \sqrt{1 - 4}}{2} = \dfrac{-1 \pm \sqrt{-3}}{2}. \nonumber\]
A problem arises immediately with this solution since there is no real number \(t\) with the property that \(t^{2} = -3\) or \(t = \sqrt{-3}\). To make sense of solutions like this we introduce complex numbers. Although complex numbers arise naturally when solving quadratic equations, their introduction into mathematics came about from the problem of solving cubic equations.
If we use the quadratic formula to solve an equation such as \(x^{2} + x + 1 = 0\),
we obtain the solutions \(x = \dfrac{-1 + \sqrt{-3}}{2}\) and \(x = \dfrac{-1 - \sqrt{-3}}{2}\). These numbers are complex numbers and we have a special form for writing these numbers. We write them in a way that that isolates the square root of \(-1\). To illustrate, the number
\[\dfrac{-1 + \sqrt{-3}}{2} \nonumber\]
can be written as follows:
\[\dfrac{-1 + \sqrt{-3}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{-3}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{3}\sqrt{-1}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}\sqrt{-1} \nonumber\]
Since there is no real number \(t\) satisfying \(t^{2} = -1\), the number \(\sqrt{-1}\) is not a real number. We call \(\sqrt{-1}\) an imaginary number and give it a special label \(i\). Thus, \(i = \sqrt{-1}\) or \(i^{2} = -1\). With this in mind we can write
\[\dfrac{-1 + \sqrt{-3}}{2} = -\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i \nonumber\]
and every complex number has this special form.
Definition: Complex Numbers
A complex number is an object of the form
\[a + bi\]
where \(a\) and \(b\) are real numbers and \(i^{2} = -1\).
The form \(a + bi\), where a and b are real numbers is called the standard form for a complex number. When we have a complex number of the form \(z = a + bi\), the number \(a\) is called the real part of the complex number \(z\) and the number \(b\) is called the imaginary part of \(z\). Since i is not a real number, two complex numbers \(a + bi\) and \(c + di\) are equal if and only if \(a = c\) and \(b = d\).
There is an arithmetic of complex numbers that is determined by an addition and multiplication of complex numbers. Adding and subtracting complex numbers is natural:
\[(a + bi) + (c + di) = (a + c) + (b + d)i\]
\[(a + bi) - (c + di) = (a - c) + (b - d)i\]
That is, to add (or subtract) two complex numbers we add (subtract)their real parts and add (subtract) their imaginary parts. Multiplication is also done in a natural way – to multiply two complex numbers, we simply expand the product as usual and exploit the fact that \(i^{2} = -1\). So the product of two complex number is
\[\begin{align*} (a + bi) + (c + di) &= ac + (ad)i + (bc)i + (bd)i^{2} \\[4pt] &= (ac - bd) + (ad + bc)i \end{align*}\]
Complex Number Properties
It can be shown that the complex numbers satisfy many useful and familiar properties, which are similar to properties of the real numbers. If \(u\), \(w\), and \(z\), are complex numbers, then
- \(w + z = z + w\)
- \(u + (w + z) = (u + w) + z\)
- The complex number \(0 = 0 + 0i\) is an additive identity, that is \(z + 0 = z\).
- If \(z = a + bi\), then the additive inverse of \(z\) is \(-z = (-a) + (-b)i\). That is, \(z + (-z) = 0\).
- \(wz = zw\)
- \(u(wz) = (uw)z\)
- \(u(w + z) = uw + uz\)
- If \(wz = 0\), then \(w = 0\) or \(z = 0\).
We will use these properties as needed. For example, to write the complex product \((1 + i)i\) in the form \(a + bi\) with \(a\) and \(b\) real numbers, we distribute multiplication over addition and use the fact that \(i^{2} = -1\) to see that
\[(1 + i)i = i + i^{2} = i + (-1) = (-1) + i.\]
For another example, if \(w = 2 + i\) and \(z = 3 - 2i\), we can use these properties to write \(wz\) in the standard \(a + bi\) form as follows:
\[wz = (2 + i)z = 2z + iz = 2(3 - 2i) + i(3 - 2i) = (6 - 4i) + (3i - 2i^{2}) = 6 - 4i + 3i - 2(-1) = 8 - i\]
Exercise \(\PageIndex{1A}\)
Write each of the sums or products as a complex number in standard form.
- \((2 + 3i) + (7 - 4i)\)
- \((4 - 2i)(3 + i)\)
- \((2 + i)i - (3 + 4i)\)
- Answer
-
(a) \((2 + 3i) + (7 - 4i) = 9 - i\)
(b) \((4 - 2i)(3 + i) = (4 - 2i)3 + (4 - 2i)i = 14 - 2i\)
(c) \((2 + i)i - (3 + 4i) = (2i - 1) - 3 - 4i = -4 - 2i\)
Exercise \(\PageIndex{1B}\)
Use the quadratic formula to write the two solutions to the quadratic equation \(x^{2} - x +2 = 0\) as complex numbers of the form \(r + si\) and \(u + vi\) for some real numbers \(r\), \(s\), \(u\), and \(v\).
(Hint: Remember: \(i = \sqrt{-1}\). So we can rewrite something like \(\sqrt{-4}\) as \(\sqrt{-4} = \sqrt{4}\sqrt{-1} = 2i\).)
- Answer
-
We use the quadratic formula to solve the equation and obtain \[x = \dfrac{1 \pm \sqrt{-7}}{2}.\]
We can then write \(\sqrt{-7} = i\sqrt{7}\). So the two solutions of the quadratic equation are:
\[\begin{align*} x &= \dfrac{1 \pm i\sqrt{7}}{2} \\[4pt] &= \dfrac{1}{2} \pm \dfrac{\sqrt{7}}{2}i \\[4pt] \end{align*}\]
Division of Complex Numbers
We can add, subtract, and multiply complex numbers, so it is natural to ask if we can divide complex numbers. We illustrate with an example.
Example \(\PageIndex{2}\): Dividing by a Complex Number
Write the quotient \(\dfrac{2 + i}{3 + i}\) as a complex number in the form \(a + bi\).
Solution
This problem is rationalizing a denominator since \(i = \sqrt{-1}\). So in this case we need to “remove” the imaginary part from the denominator. Recall that the product of a complex number with its conjugate is a real number, so if we multiply the numerator and denominator of \(\dfrac{2 + i}{3 + i}\) by the complex conjugate of the denominator, we can rewrite the denominator as a real number. The steps are as follows. Multiplying the numerator and denominator by the conjugate \(3 - i\) or \(3 + i\) gives us
\[\dfrac{2 + i}{3 + i} = \left(\dfrac{2 + i}{3 + i}\right)\left(\dfrac{3 - i}{3 - i}\right) = \dfrac{(2 + i)(3 - i)}{(3 + i)(3 - i)} = \dfrac{(6 - i^{2}) + (-2 + 3)i}{9 - i^{2}} = \dfrac{7 + i}{10} \nonumber\]
Now we can write the final result in standard form as
\[\dfrac{7 + i}{10} = \dfrac{7}{10} + \dfrac{1}{10}i. \nonumber\]
Example \(\PageIndex{2}\) illustrates the general process for dividing one complex number by another. In general, we can write the quotient \(\dfrac{a + bi}{c + di}\) in the form \(r + si\) by multiplying numerator and denominator of our fraction by the conjugate \(c - di\) of \(c + di\) to see that
\[\dfrac{a + bi}{c + di} = \left(\dfrac{a + bi}{c + di}\right)\left(\dfrac{c - di}{c - di}\right) = \dfrac{(ac + bd) + (bc - ad)i}{c^{2} + d^{2}} = \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}}i\]
Therefore, we have the formula for the quotient of two complex numbers.
Definition: Quotient of Complex Numbers
The quotient \(\dfrac{a + bi}{c + di}\) of the complex numbers \(a + bi\) and \(c + di\) is the complex number
\[\dfrac{a + bi}{c + di} = \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}}i\]
provided \(c + di \neq 0\).
Exercise \(\PageIndex{3}\)
Let \(z = 3 + 4i\) and \(w = 5 - i\).
- Write \(\dfrac{w}{z} = \dfrac{5 - i}{3 + 4i}\) as a complex number in the form \(r + si\) where \(r\) and \(s\) are some real numbers. Check the result by multiplying the quotient by \(3 + 4i\). Is this product equal to \(5 - i\)?
- Find the solution to the equation \((3 + 4i)x = 5 - i\) as a complex number in the form \(x = u + vi\) where \(u\) and \(v\) are some real numbers.
- Answer
-
- Using our formula with \(a = 5, b = -1, c = 3\) and \(d = 4\) gives us \[\dfrac{5 - i}{3 + 4i} = \dfrac{15 - 4}{15} + \dfrac{-3 -20}{25}i = \dfrac{11}{25} - \dfrac{23}{25}i\] As a check, we see that \[\left(\dfrac{11}{25} - \dfrac{23}{25}i\right)\left(3 + 4i\right) = \left(\dfrac{33}{25} - \dfrac{69}{25}i\right) + \dfrac{44}{25}i - \dfrac{92}{25}i^{2} = \left(\dfrac{33}{25} + \dfrac{92}{25}\right) + \left(-\dfrac{69}{25}i + \dfrac{44}{25}i\right) = 5 - i\]
- We can solve for \(x\) by dividing both sides of the equation by \(3 + 4i\) to see that \[x = \dfrac{5 - i}{3 + 4i} = \dfrac{11}{25} - \dfrac{23}{25}i\]
Geometric Representations of Complex Numbers
Each ordered pair \((a , b)\) of real numbers determines:
- A point in the coordinate plane with coordinates \((a , b)\).
- A complex number \(a + bi\)
- A vector \(a\textbf{i} + b\textbf{j} = ( a, b )\)
This means that we can geometrically represent the complex number \(a + bi\) with a vector in standard position with terminal point \((a , b)\). Therefore, we can draw pictures of complex numbers in the plane. When we do this, the horizontal axis is called the real axis, and the vertical axis is called the imaginary axis. In addition, the coordinate plane is then referred to as the complex plane. That is, if \(z = a + b i\), we can think of \(z\) as a directed line segment from the origin to the point (a, b), where the terminal point of the segment is \(a\) units from the imaginary axis and \(b\) units from the real axis. For example, the complex numbers \(3 + 4i\) and \(-8 + 3i\) are shown in Figure 5.1.
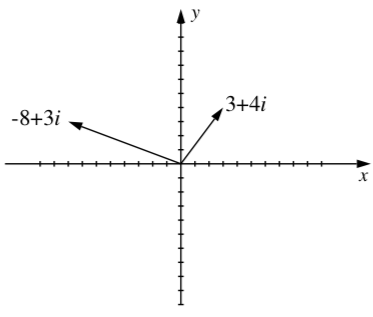
Figure \(\PageIndex{1}\): Two complex numbers.
In addition, the sum of two complex numbers can be represented geometrically using the vector forms of the complex numbers. Draw the parallelogram defined by \(w = a + bi\) and \(z = c + di\). The sum of \(w\) and \(z\) is the complex number represented by the vector from the origin to the vertex on the parallelogram opposite the origin as illustrated with the vectors \(w = 3 + 4i\) and \(z = -8 + 3i\) in Figure \(\PageIndex{2}\).
Exercise \(\PageIndex{4}\)
Let \(w = 2 + 3i\) and \(z = -1 + 5i\).
- Write the complex sum \(w + z\) in standard form.
- Draw a picture to illustrate the sum using vectors to represent \(w\) and \(z\).
- Answer
-
1. The sum is \(w + z = (2 - 1) + (3 + 5)i = 1 + 8i\).
2. A representation of the complex sum using vectors is shown in the figure below.
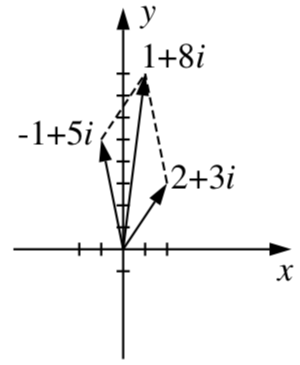
We now extend our use of the representation of a complex number as a vector in standard position to include the notion of the length of a vector. Recall from Section 3.6 that the length of a vector \(\textbf{v} = a\textbf{i} + b\textbf{j}\) is \(|\textbf{v}| = \sqrt{a^{2} + b^{2}}\).
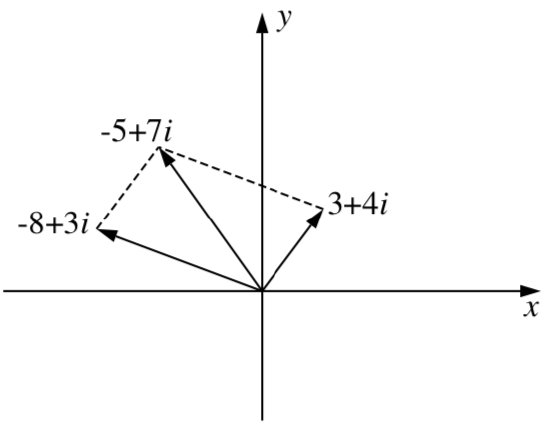
Figure \(\PageIndex{2}\): The Sum of Two Complex Numbers.
When we use this idea with complex numbers, we call it the norm or modulus of the complex number.
Definition: Norm
The norm (or modulus) of the complex number \(z = a + bi\) is the distance from the origin to the point \((a, b)\) and is denoted by \(|z|\). We see
that \[|z| = |a + bi| = \sqrt{a^{2} + b^{2}}.\]
There is another concept related to complex number that is based on the following bit of algebra.
\[(a + bi)(a -bi) = a^{2} - (bi)^{2} = a^{2} - b^{2}i^{2} = a^{2} + b^{2}\]
The complex number \(a - bi\) is called the complex conjugate of \(a + bi\). If we let \(z = a + bi\), we denote the complex conjugate of \(z\) as \(\bar{z}\). So \[\bar{z} = \overline{a + bi} = a - bi.\]
We also notice that
\[z\bar{z} = (a + bi)(a - bi) = a^{2} + b^{2},\]
and so the product of a complex number with its conjugate is a real number. In fact,
\[z\bar{z} = a^{2} + b^{2} = |z|^{2},\], and so \[|z| = \sqrt{z\bar{z}}\]
Exercise \(\PageIndex{5}\)
Let \(w = 2 + 3i\) and \(z = -1 + 5i\)
- Find \(\bar{w}\) and \(\bar{z}\).
- Compute \(|w|\) and \(|z|\).
- Compute \(w\bar{w}\) and \(z\bar{z}\).
- What is \(\bar{z}\) if \(z\) is a real number?
- Answer
-
1. Using the definition of the conjugate of a complex number we find that \(\bar{w} = 2 - 3i\) and \(\bar{z} = -1 - 5i\).
2. Using the definition of the norm of a complex number we find that \(|w| = \sqrt{2^{2} + 3^{2}} = \sqrt{13}\) and \(|z| = \sqrt{(-1)^{2} + 5^{2}} = \sqrt{26}\).
3. Using the definition of the product of complex numbers we find that\[w\bar{w} = (2 + 3i)(2 - 3i) = 4 + 9 = 13\]
\[z\bar{z} = (-1 + 5i)(-1 - 5i) = 1 + 25 = 26\]
4. Let \(z = a + 0i\) for some \(a \in \mathbb{R}\). Then \(\bar{z} = a - 0i\). Thus, \(\bar{z} = z\) when \(z \in \mathbb{R}\).
Summary
In this section, we studied the following important concepts and ideas:
- A complex number is an object of the form \(a + bi\), where \(a\) and \(b\) are real numbers and \(i^{2} = -1\). When we have a complex number of the form \(z = a + bi\), the number \(a\) is called the real part of the complex number \(z\) and the number \(b\) is called the imaginary part of \(z\).
- We can add, subtract, multiply, and divide complex numbers as follows:
\[(a + bi) + (c + di) = (a + c) + (b + d)i \nonumber \]
\[(a + bi) - (c + di) = (a - c) + (b - d)i\nonumber\]
\[(a + bi)(c + di) = (ac - bd) + (ad + bc)i\nonumber\]
\[\dfrac{a + bi}{c + di} = \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}}i\nonumber\] provided \(c + di \neq 0\)
- A complex number \(a + bi\) can be represented geometrically with a vector in standard position with terminal point \((a, b)\). When we do this, the horizontal axis is called the real axis, and the vertical axis is called the imaginary axis. In addition, the coordinate plane is then referred to as the complex plane. That is, if \(z = a + bi\) we can think of \(z\) as a directed line segment from the origin to the point \((a, b)\), where the terminal point of the segment is a units from the imaginary axis and \(b\) units from the real axis.
- The norm (or modulus) of the complex number \(z = a + bi\) is the distance from the origin to the point \((a, b)\) and is denoted by \(|z|\). We see that \[|z| = |a + bi| = \sqrt{a^{2} + b^{2}} \nonumber\]
- The complex number \(a - bi\) is called the complex conjugate of \(a + bi\). Note that \[(a + bi)(a - bi) = a^{2} + b^{2} = |a + bi|^{2} \nonumber\]


