5.4: The Polar Coordinate System
- Page ID
- 7127
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- How are the polar coordinates of a point in the plane determined?
- How do we convert from polar coordinates to rectangular coordinates?
- How do we convert from rectangular to polar coordinates?
- How doe we correctly graph polar equations both by hand and with a calculator?
Beginning Activity
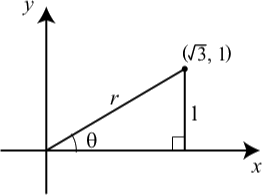
In the diagram, the point with coordinates \((\sqrt{3}, 1)\) has been plotted. Determine the value of \(r\) and the angle \(\theta\) in radians and degrees.
In our study of trigonometry so far, whenever we graphed an equation or located a point in the plane, we have used rectangular (or Cartesian) coordinates. The use of this type of coordinate system revolutionized mathematics since it provided the first systematic link between geometry and algebra. Even though the rectangular coordinate system is very important, there are other methods of locating points in the plane. We will study one such system in this section.
Rectangular coordinates use two numbers (in the form of an ordered pair) to determine the location of a point in the plane. These numbers give the position of a point that corresponds to the ordered pair \((\sqrt{3}, 1)\), we start at the origin and travel \(\sqrt{3}\) units to the right and then travel \(1\) unit up. The idea of the polar coordinate system is to give a distance to travel and an angle in which direction to travel. We reach the same point as the one given by the rectangular coordinates \((\sqrt{3}, 1)\) by saying we will travel 2 units at an angle of \(30^\circ\) from the \(x\)-axis. These values correspond to the values of \(r\) and \(\theta\) in the diagram for the beginning activity. Using the Pythagorean Theorem, we can obtain \(r = 2\) and using the fact that \(\sin(\theta) = \dfrac{1}{2}\), we see that \(\theta = \dfrac{\pi}{6}\) radians or \(30^\circ\).
The Polar Coordinate System
For the rectangular coordinate system, we use two numbers, in the form of an ordered pair, to locate a point in the plane. We do the same thing for polar coordinates, but now the first number represents a distance from a point and the second number represents an angle. In the polar coordinate system, we start with a point \(O\), called the pole and from this point, we draw a horizontal ray (directed half-line) called the polar axis. We can then assign polar coordinates \(r, \theta\) to a point \(P\) in the plane as follows (see Figure 5.5):
- The number \(r\), called the radial distance, is the directed distance from the pole to the point \(P\).
- The number \(\theta\), called the polar angle, is the measure of the angle from the polar axis to the line segment \(OP\). (Either radians or degrees can be used for the measure of the angle.)
Conventions for Polar Coordinates
The polar angle \(\theta\) is considered positive if measured in a counterclockwise direction from the polar axis.
The polar angle \(\theta\) is considered negative if measured in a clockwise direction from the polar axis.
If the radial distance \(r\) is positive, then the point \(P\) is \(r\) units from \(O\) along the terminal side of \(\theta\).
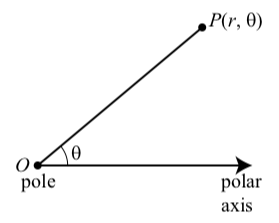
Figure \(\PageIndex{1}\): Polar Coordinates
If the radial distance \(r\) is negative, then the point \(P\) is \(|r\) units from \(O\) along the ray in the opposite direction as the terminal side of \(\theta\).
If the radial distance \(r\) is zero, then the point \(P\) is the point \(O\).
To illustrate some of these conventions, consider the point \(P(3, \dfrac{4\pi}{3})\) shown on the left in Figure \(\PageIndex{2}\). (Notice that the circle of radius \(3\) with center at the pole has been drawn.)
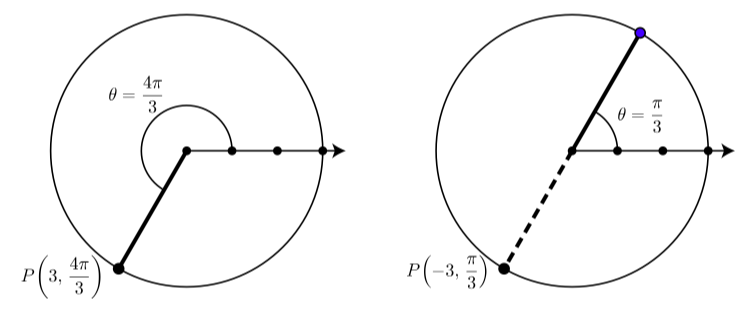
Figure \(\PageIndex{2}\): A Point with Two Different Sets of Polar Coordinates
The diagram on the right in Figure \(\PageIndex{2}\) illustrates that this point \(P\) also has polar coordinates \(P(-3, \dfrac{\pi}{3})\). This is because when we use the polar angle \(\theta = \dfrac{\pi}{3}\) and the radial distance \(r = -3\), then the point \(P\) is \(3\) units from the pole along the ray in the opposite direction as the terminal side of \(\theta\).
Exercise \(\PageIndex{1}\)
Since a point with polar coordinates \((r, \theta)\) must lie on a circle of radius r with center at the pole, it is reasonable to locate points on a grid of concentric circles and rays whose initial point is at the pole as shown in Figure \(\PageIndex{3}\). On this polar graph paper, each angle increment is \(\dfrac{\pi}{12}\) radians. For example, the point \((4, \dfrac{\pi}{6})\) is plotted in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): Polar Graph Paper
Plot the following points with the specified polar coordinates.
\[(1, \dfrac{\pi}{4}), (5, \dfrac{\pi}{4}), (2, \dfrac{\pi}{3}), (3, \dfrac{5\pi}{4}), (4, -\dfrac{\pi}{4}), (4, \dfrac{7\pi}{4}), (6, \dfrac{5\pi}{6}), (5, \dfrac{9\pi}{4}), (-5, \dfrac{5\pi}{4})\]
- Answer
-

In Exercise \(\PageIndex{1}\), we noticed that the polar coordinates \((5, \dfrac{\pi}{4}), (5, \dfrac{9\pi}{4})\), and \((-5, \dfrac{5\pi}{4})\)all determined the same point in the plane. This illustrates a major difference between rectangular coordinates and polar coordinates. Whereas each point has a unique representation in rectangular coordinates, a given point can have many different representations in polar coordinates. This is primarily due to the fact that the polar coordinate system uses concentric circles for its grid, and we can start at a point on a circle and travel around the circle and end at the point from which we started. Since one wrap around a circle corresponds to an angle of \(2\pi\) radians or \(360^\circ\), we have the following:
Polar Coordinates of a Point
A point \(P\), other than the pole, determined by the polar coordinates \((r, \theta)\) is also determined by the following polar coordinates:
In radians:
\[(r, \theta + k(2\pi))\] \[(-r, \theta + (2k + 1)\pi)\]
In degrees:
\[(r, \theta + k(360^\circ))\] \[(-r, \theta + (2k + 1)180^\circ)\]
where \(k\) can be any integer.
If the point \(P\) is the pole, the its polar coordinates are \((0, \theta)\) for any polar angle \(\theta\).
Exercise \(\PageIndex{2}\)
Find four different representations in polar coordinates for the point with polar coordinates \((3, 110^\circ)\). Use a positive value for the radial distance \(r\) for two of the representations and a negative value for the radial distance \(r\) for the other two representations.
- Answer
-
The left column shows some sets of polar coordinates with a positive value for \(r\) and the right column shows some sets of polar coordinates with a negative value for \(r\).
\[(3, 470^\circ)\]
\[(-3, 290^\circ)\]
\[(3, 830^\circ)\]
\[(-3, 650^\circ)\]
\[(3, -250^\circ)\]
\[(-3, -70^\circ)\]
\[(3, -510^\circ)\]
\[(-3, -430^\circ)\]
\[(3, 1190^\circ)\]
\[(-3, 1010^\circ)\]
Conversions Between Polar and Rectangular Coordinates
We now have two ways to locate points in the plane. One is the usual rectangular (Cartesian) coordinate system and the other is the polar coordinate system. The rectangular coordinate system uses two distances to locate a point, whereas the polar coordinate system uses a distance and an angle to locate a point. Although these two systems can be studied independently of each other, we can set them up so that there is a relationship between the two types of coordinates. We do this as follows:
- We place the pole of the polar coordinate system at the origin of the rectangular coordinate system.
- We have the polar axis of the polar coordinate system coincide with the positive \(x\)-axis of the rectangular coordinate system as shown in Figure \(\PageIndex{4}\)
Using right triangle trigonometry and the Pythagorean Theorem, we obtain the following relationships between the rectangular coordinates \((x, y)\) and the polar coordinates \((r, \theta)\):
\[\cos(\theta) = \dfrac{x}{r}\] \[x = r\cos(\theta)\]
\[\sin(\theta) = \dfrac{y}{r}\] \[y = r\sin(\theta)\]
\[\tan(\theta) = \dfrac{y}{x}\] if \(x \neq 0\) \[x^{2} + y^{2} = r^{2}\]
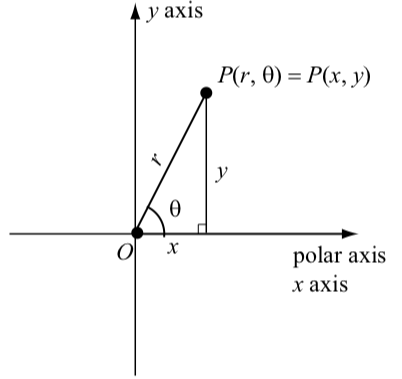
Figure \(\PageIndex{4}\): Polar and Rectangular Coordinates coordinates
Coordinate Conversion
To determine the rectangular coordinates \((x, y)\) of a point whose polar coordinates \((r, \theta)\) are known, use the equations
\[x = r\cos(\theta)\] \[y = r\sin(\theta)\]
To determine the polar coordinates \((r, \theta)\) of a point whose rectangular coordinates \((x, y)\) are known, use the equation \(r^{2} = x^{2} + y^{2}\) to determine \(r\) and determine an angle \(\theta\) so that
\[\tan(\theta) = \dfrac{y}{x}\] if \(x \neq 0\)
\[\cos(\theta) = \dfrac{x}{r}\]
\[\sin(\theta) = \dfrac{y}{r}\]
When determining the polar coordinates of a point, we usually choose the positive value for \(r\). We can use an inverse trigonometric function to help determine \(\theta\) but we must be careful to place \(\theta\) in the proper quadrant by using the signs of \(x\) and \(y\). Note that if \(x = 0\), we can use \(\theta = \dfrac{\pi}{2}\) or \(\theta = \dfrac{3\pi}{2}\)
Exercise \(\PageIndex{3}\)
Determine rectangular coordinates for each of the following points in polar coordinates:
\[(3, \dfrac{\pi}{3})\] \[(5, \dfrac{11\pi}{6})\] \[(-5, \dfrac{3\pi}{4})\]
When we convert from rectangular coordinates to polar coordinates, we must be careful and use the signs of \(x\) and \(y\) to determine the proper quadrant for the angle \(\theta\). In many situations, it might be easier to first determine the reference angle for the angle \(\theta\) and then use the signs of \(x\) and \(y\) to determine \(\theta\).
- Answer
-
For each point, we use the equations \(x = r\cos(\theta)\) and \(y = r\sin(\theta)\). In each of these cases, we can determine the exact values for \(x\) and \(y\).
Polar Coordinates Rectangular Coordinates 1. \((3, \dfrac{\pi}{3})\) \((\dfrac{3}{2}, \dfrac{3\sqrt{3}}{2})\) 2. \((5, \dfrac{11\pi}{6})\) \((\dfrac{5\sqrt{3}}{2}, -\dfrac{5}{2})\) 3. \((-5, \dfrac{3\pi}{4})\) \((\dfrac{5\sqrt{2}}{2}, -\dfrac{5\sqrt{2}}{2})\)
Example \(\PageIndex{1}\): (Converting from Rectangular to Polar Coordinates)
To determine polar coordinates for the the point \((-2, 2)\) in rectangular coordinates, we first draw a picture and note that
\[r^{2} = (-2)^{2} + 2^{2} = 8 \nonumber\]
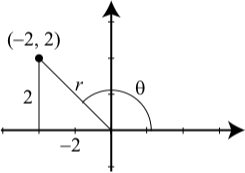
Since it is usually easier to work with a positive value for \(r\), we will use \(r = \sqrt{8}\).
We also see that \(\tan(\theta) = \dfrac{3}{-3} = -1\). We can use many different values for \(\theta\) but to keep it easy, we use \(\theta\) as shown in the diagram. For the reference angle \(\hat{\theta}\), we have \(\tan(\hat{\theta}) = 1\) and so \(\hat{\theta} = \dfrac{\pi}{4}\). Since \(-2 < 0\) and \(2 > 0\), \(\theta\) is in the second quadrant, and we have \[\theta = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\]
So the point \((-2, 2)\) in rectangular coordinates has polar coordinates \((\sqrt{8}, \dfrac{3\pi}{4})\).
Exercise \(\PageIndex{4}\)
Determine polar coordinates for each of the following points in rectangular coordinates:
\[(6, 6\sqrt{3})\] \[(0, -4)\] \[(-4, 5)\]
In each case, use a positive radial distance \(r\) and a polar angle \(\theta\) with \(0 \leq \theta \leq 2\pi\).
An inverse trigonometric function will need to be used for (3).
- Answer
-
1. For the point \((6, 6\sqrt{3}), r^{2} = 6^{2} + (6\sqrt{3})^{2} = 144\) and so \(r = 12\). Since the point is in the first quadrant, we can use \(\tan(\theta) = \sqrt{3}\) or \(\cos(\theta) = \dfrac{1}{2}\) to conclude that \(\theta = \dfrac{\pi}{3}\). So the polar coordinates are \((12, \dfrac{\pi}{3})\).
2. For the point \((0, -4)\), \(r^{2} = 0^{2} + (-4)^{2} = 16\) and so \(r = 4\). Since the point is on the \(y\)-axis, we can use \(\cos(\theta) = 0\) and \(\sin(\theta) - 1\) to conclude that \(\theta = \dfrac{3\pi}{2}\). So the polar coordinates are \((4, \dfrac{3\pi}{2})\).
3. For the point \((-4, 5\sqrt{3}), r^{2} = (-4)^{2} + 5^{2} = 41\) and so \(r = \sqrt{41}\). Since the point is in the second quadrant, we can use \(\tan(\theta) = -1.25\) to conclude that the reference angle is \(\hat{\theta} = \tan^{-1}(-1.25)\). We cannot determine an exact value for \(\theta\) and so we can say that the polar coordinates are \((\sqrt{41}, \pi - \tan^{-1}(1.25))\). We can also approximate the angle and see that the approximate polar coordinates are \((\sqrt{41}, 2.24554)\). Note: There are other ways to write the angle \(\theta\). It is true that \(\theta = \pi - \cos^{-1}(\dfrac{4}{\sqrt{21}}) = \cos^{-1}(\dfrac{-4}{\sqrt{21}})\).
The Graph of a Polar Equation
The graph an equation on the rectangular coordinate system consists of all points \((x, y)\) that satisfy the equation. The equation can often be written in the form of a function such as \(y = f(x)\) In this case, a point \((a, b)\) is on the graph of this function if and only if \(b = f(a)\) In a similar manner,
Definition
An equation whose variables are polar coordinates (usually \(r\) and \(\theta\)) is called a polar equation. The graph of a polar equation is the set of all points whose polar coordinates \((r, \theta)\) satisfy the given equation.
An example of a polar equation is \(r = 4\sin(\theta)\). For this equation, notice that
- If \(\theta = 0\), then \(r = 4\sin(0) = 0\) and so the point \((0, 0)\) (in polar coordinates) is on the graph of this equation.
- If \(\theta = \dfrac{\pi}{6}\), then \(r = 4\sin(\dfrac{\pi}{6}) = 4\cdot \dfrac{1}{2} = 2\) and so \((2, \dfrac{\pi}{6})\) is on the graph of this equation. (Remember: for polar coordinates, the value of \(r\) is the first coordinate.)
The most basic method for drawing the graph of a polar equation is to plot the points that satisfy the polar equation on polar graph paper as shown in Figure \(\PageIndex{4}\) and then connect the points with a smooth curve.
Exercise \(\PageIndex{5}\)
The following table shows the values of \(r\) and \(\theta\) for points that are on the graph of the polar equation \(r = 4\sin(\theta)\).
| \(r = 4\sin(\theta)\) | \(\theta\) |
|---|---|
| 0 | 0 |
| 2 | \(\dfrac{\pi}{6}\) |
| \(2\sqrt{2}\) | \(\dfrac{\pi}{4}\) |
| \(2\sqrt{3}\) | \(\dfrac{\pi}{3}\) |
| 4 | \(\dfrac{\pi}{2}\) |
| \(2\sqrt{3}\) | \(\dfrac{2\pi}{3}\) |
| \(2\sqrt{2}\) | \(\dfrac{3\pi}{4}\) |
| 2 | \(\dfrac{5\pi}{6}\) |
| 0 | \(\pi\) |
Plot these points on polar graph paper and draw a smooth curve through the points for the graph of the equation \(r = 4\sin(\theta)\).

- Answer
-

Depending on how carefully we plot the points and how well we draw the curve, the graph in Exercise \(\PageIndex{5}\) could be a circle. We can, of course, plot more points. In fact, in Exercise \(\PageIndex{5}\), we only used values for \(\theta\) with \(0 \leq \theta \leq \pi\). The following table shows the values of \(r\) and \(\theta\) for points that are on the graph of the polar equation \(r = 4\sin(\theta)\) with \(\pi \leq \theta \leq 2\pi\).
| \(r = 4\sin(\theta)\) | \(\theta\) |
|---|---|
| 0 | \(\pi\) |
| -2 | \(\dfrac{7\pi}{6}\) |
| \(-2\sqrt{2}\) | \(\dfrac{5\pi}{4}\) |
| \(-2\sqrt{3}\) | \(\dfrac{4\pi}{3}\) |
| -4 | \(\dfrac{3\pi}{2}\) |
| \(-2\sqrt{3}\) | \(\dfrac{5\pi}{3}\) |
| \(-2\sqrt{2}\) | \(\dfrac{7\pi}{4}\) |
| -2 | \(\dfrac{11\pi}{6}\) |
| 0 | \(\pi\) |
Because of the negative values for \(r\), if we plot these points, we will get the same points we did in Exercise \(\PageIndex{4}\). So a good question to ask is, “Do these points really lie on a circle?” We can answer this question by converting the equation \(r = 4\sin(\theta)\) into an equivalent equation with rectangular coordinates.
Transforming an Equation from Polar Form to Rectangular Form
The formulas that we used to convert a point in polar coordinates to rectangular coordinates can also be used to convert an equation in polar form to rectangular form. These equations are given in the box on page 326. So let us look at the equation \(r = 4\sin(\theta)\) from Exercise \(\PageIndex{5}\).
Exercise \(\PageIndex{6}\)
We start with the equation \(r = 4\sin(\theta)\). We want to transform this into an equation involving \(x\) and \(y\). Since \(r^{2} = x^{2} + y^{2}\), it might be easier to work with \(r^{2}\) rather than \(r\).
- Multiply both sides of the equation \(r = 4\sin(\theta)\) by \(r\).
- Now use the equations \(r^{2} = x^{2} + y^{2}\) to obtain an equivalent equation in \(x\) and \(y\).
- Answer
-
1. \(r^{2} = 4r\sin(\theta)\)
2. \(x^{2} + y^{2} = 4y\)
The graph of the equation the graph of \(r = 4\sin(\theta)\) in polar coordinates will be the same as the graph of \(x^{2} + y^{2} = 4y\) in rectangular coordinates. We can now use some algebra from previous mathematics courses to show that this is the graph of a circle. The idea is to collect all terms on the left side of the equation and use completing the square for the terms involving \(y\).
As a reminder, if we have the expression \(t^{2} + at = 0\), we complete the square by adding \((\dfrac{a}{2})^{2}\) to both sides of the equation. We will then have a perfect square on the left side of the equation.
\[t^{2} + at + (\dfrac{a}{2})^{2} = (\dfrac{a}{2})^{2}\]
\[t^{2} + at + \dfrac{a^{2}}{4} = \dfrac{a^{2}}{4}\]
\[(t + \dfrac{a}{2})^ {2} = \dfrac{a^{2}}{4}\]
So for the equation \(x^{2} + y^{2} = 4y\), we have
\[x^{2} + y^{2} - 4y = 0\]
\[x^{2} + y^{2} 4y + 4 = 4\]
\[x^{2} + (y - 2)^{2} = 2^{2}\]
This is the equation (in rectangular coordinates) of a circle with radius \(2\) and center at the point \((0, 2)\). We see that this is consistent with the graph we obtained in Exercise \(\PageIndex{5}\).
Exercise \(\PageIndex{7}\)
Transform the equation \(r = 6\cos(\theta)\) into an equation in rectangular coordinates and then explain why the graph of \(r = 6\cos(\theta)\) is a circle. What is the radius of this circle and what is its center?
- Answer
-
\[r^{2} = 6r\sin(\theta), x^{2} + y^{2} = 6x\]
\[x^{2} - 6x + 9 + y^{2} = 9, (x - 3)^{2} + y^{2} = 3^{2}\]
So the graph of \(r = 3\cos(\theta)\) is a circle with radius \(3\) and center at \((3, 0)\).
The Polar Grid
We introduced polar graph paper in Figure 5.7. Notice that this consists of concentric circles centered at the pole and lines that pass through the pole. These circles and lines have very simple equations in polar coordinates. For example:
- Consider the equation \(r = 3\). In order for a point to be on the graph of this equation, it must lie on a circle of radius 3 whose center is the pole. So the graph of this equation is a circle of radius 3 whose center is the pole. We can also show this by converting the equation \(r = 3\) to rectangular form as follows:
\[r = 3\]
\[r^{2} = 3^{2}\]
\[x^{2} + y^{2} = 9\]
In rectangular coordinates, this is the equation of a circle of radius 3 centered at the origin.
- Now consider the equation \(\theta= \dfrac{\pi}{4}\). In order for a point to be on the graph of this equation, the line through the pole and this point must make an angle of \(\dfrac{\pi}{4}\) radians with the polar axis. If we only allow positive values for \(r\), the graph will be a ray with initial point at the pole that makes an angle of \(\dfrac{\pi}{4}\) radians with the polar axis. However, if we allow \(r\) to be any real number, then we obtain the line through the pole that makes an angle of \(\dfrac{\pi}{4}\) radians with the polar axis. We can convert this equation to rectangular coordinates as follows:
\[\theta = \dfrac{\pi}{4}\]
\[\tan(\theta) = \tan(\dfrac{\pi}{4})\]
\[\dfrac{y}{x} = 1\]
\[y = x\]
This is an equation for a straight line through the origin with a slope of 1.
In general:
Definition
- If \(a\) is a positive real number, then the graph of \(r = a\) is a circle of radius \(a\) whose center is the pole.
- If \(b\) is a real number, then the graph of \(\theta = b\) is a line through the pole that makes an angle of \(b\) radians with the polar axis.
Concluding Remarks
We have studied just a few graphs of polar equations. There are many interesting graphs that can be generated using polar equations that are very difficult to accomplish in rectangular coordinates. Since the polar coordinate system is based on concentric circles, it should not be surprising that circles with center at the pole would have “simple” equations like \(r = a\).
In Exercise \(\PageIndex{5}\) and \(\PageIndex{7}\), we saw polar equations whose graphs were circles with centers not at the pole. These were special cases of the following:
Polar Equations Whose Graphs Are Circles
If \(a\) is a positive real number, then
The graph of \(r = 2a\sin(\theta)\) is a circle of radius \(a\) with center at the point \((0, a)\) in rectangular coordinates or \((a, \dfrac{\pi}{2})\) in polar coordinates.
The graph of \(r = 2a\sin(\theta)\) is a circle of radius \(a\) with center at the point \((a, 0)\) in rectangular coordinates or \((a, 0)\) in polar coordinates.
We will explore this and the graphs of other polar equations in the exercises.


