4.4: Double and Half Angle Identities

Focus Questions

The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.

• What are the Double Angle Identities for the sine, cosine, and tangent?
• What are the Half Angle Identities for the sine, cosine, and tangent?
• What are the Product-to-Sum Identities for the sine and cosine?
• What are the Sum-to-Product Identities for the sine and cosine?
• Why are these identities useful?

The sum and difference identities can be used to derive the double and half angle identities as well as other identities, and we will see how in this section. Again, these identities allow us to determine exact values for the trigonometric functions at more points and also provide tools for solving trigonometric equations (as we will see later).

Beginning Activity

1. Use \(B = A\) in the Cosine Sum Identity \[\cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B)\] to write \(\cos(2A)\) in terms of \(\cos(A)\) and \(\sin(A)\).
2. Is the equation \[\dfrac{\cos(2x)}{2} = \cos(x)\] an identity? Verify your answer.

The Double Angle Identities

Suppose a marksman is shooting a gun with muzzle velocity \(v_{0} = 1200\) feet per second at a target \(1000\) feet away. If we neglect all forces acting on the bullet except the force due to gravity, the horizontal distance the bullet will travel depends on the angle \(\theta\) at which the gun is fired. If we let \(r\) be this horizontal distance (called the range), then \[r = \dfrac{v_{0}^{2}}{g}\sin(2\theta),\]

where \(g\) is the gravitational force acting to pull the bullet downward. In this context, \(g = 32\) feet per second squared, giving us

\[r = 45000\sin(2\theta)\]

The marksman would want to know the minimum angle at which he should fire in order to hit the target \(1000\) feet away. In other words, the marksman wants to determine the angle \(\theta\) so that \(r = 1000\). This leads to solving the equation

\[45000\sin(2\theta) = 1000\]

Equations like the range equation in which multiples of angles arise frequently, and in this section we will determine formulas for \(\cos(2A)\) and \(\sin(2A)\) in terms of \(\cos(A)\) and \(\sin(A)\). These formulas are called double angle identities. In our Beginning Activity we found that

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]
can be derived directly from the Cosine Sum Identity. A similar identity for the

sine can be found using the Sine Sum Identity:

\[\sin(2A) = \sin(A + A) = \sin(A)\cos(A) + \cos(A)\sin(A) = 2\cos(A)\sin(A).\]

Exercise \(\PageIndex{1}\)

If \(\cos(\theta) = \dfrac{5}{13}\) and \(\dfrac{3\pi}{2} \leq \theta \leq 2\pi\), find \(\cos(2\theta)\) and \(\sin(2\theta)\).

Answer

We are assuming that \(\cos(\theta) = \dfrac{5}{13}\) and \(\dfrac{3\pi}{2} \leq \theta \leq 2\pi\). To determine \(\cos(2\theta)\) and \(\sin(2\theta)\), we will use the double angle indentities.
\[\cos(2\theta) = \cos^{2}(\theta) - \sin^{2}(\theta)\]

\[\sin(2\theta) = 2\cos(\theta)\sin(\theta)\]

To use these identities, we also need to know \(\sin(\theta)\). So we use the Pythagorean identity.

\[\cos^{2}(\theta) + \sin^{2}(\theta) = 1\]

\[\sin^{2}(\theta) = 1 - \cos^{2}(\theta) = 1 - (\dfrac{5}{13})^{2} = \dfrac{144}{169}\]

Since \(\dfrac{3\pi}{2} \leq \theta \leq 2\pi\), we see that \(\sin(\theta) < 0\) and so \(\sin(\theta) = -\dfrac{12}{13}\). Hence,

\[\cos(2\theta) = \cos^{2}(\theta) - \sin^{2}(\theta) = (\dfrac{5}{13})^{2} - (-\dfrac{12}{13})^{2} = -\dfrac{119}{169}\]

\[\sin(2\theta) = 2\cos(\theta)\sin(\theta) = 2(\dfrac{5}{13})(-\dfrac{12}{13}) = -\dfrac{120}{169}\]

There is also a double angle identity for the tangent. We leave the verification of that identity for the exercises. To summarize:

Double Angle Identities

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]

\[\sin(2A) = 2\cos(A)\sin(A)\]

\[\tan(2A) = \dfrac{2\tan(A)}{1 - \tan^{2}(A)}\]

The first two identities are valid for all numbers \(A\) and the third is valid as long as \(A \neq \dfrac{\pi}{4} + k(\dfrac{\pi}{2})\), where \(k\) is an integer.

Exercise \(\PageIndex{2}\)

Prove the alternate versions of the double angle identity for the cosine.

1. \(\cos(2A) = 1 - 2\sin^{2}(A)\)
2. \(\cos(2A) = 2\cos^{2}(A) - 1\)

Answer

We will prove alternate forms of the double angle identity for cosine.

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A) = (1 - \sin^{2}(A)) - \sin^{2}(A) = 1 - \sin^{2}(A) - \sin^{2}(A) = 1 - 2\sin^{2}(A)\]

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A) = \cos^{2}(A) - (1 - \cos^{2}(A)) = \cos^{2}(A) - 1 + \cos^{2}(A) = 2\cos^{2}(A) - 1\]

Solving Equations with Double Angles

Solving equations, like \(45000\sin(2\theta) = 1000\), that involve multiples of angles, requires the same kind of techniques as solving other equations, but the multiple angle can add another wrinkle.

Example \(\PageIndex{1}\): (Solving an Equation with a Multiple Angle)

Consider the equation \[2\cos(2\theta) - 1 = 0\]
This is an equation that is linear in \(\cos(2\theta)\), so we can apply the same ideas as we did earlier to this equation. We solve for \(\cos(2\theta)\) to see that

\[\cos(2\theta) = \dfrac{1}{2}.\]

We know the angles at which the cosine has the value \(\dfrac{1}{2}\), namely \(\dfrac{\pi}{3} + 2\pi k\) and \(-\dfrac{\pi}{3} + 2\pi k\) for integers \(k\). In our case, this make
\[2\theta = \dfrac{\pi}{3} + 2\pi k\] or \[2\theta = -\dfrac{\pi}{3} + 2\pi k\]
for integers \(k\).

Now we divide by \(2\) to find our solutions

\[\theta = \dfrac{\pi}{6} + \pi k\] or \[\theta = -\dfrac{\pi}{6} + \pi k\]

These solutions are illustrated in Figure \(\PageIndex{1}\).

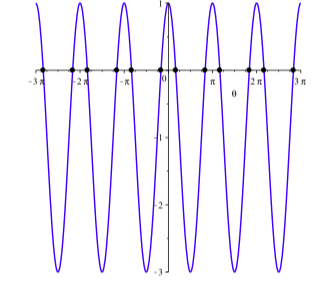
Figure \(\PageIndex{1}\): Graphs of \(y = 2\cos(2\theta) - 1\).

Exercise \(\PageIndex{3}\)

Approximate the smallest positive solution in degrees, to two decimal places, to the range equation

\[45000\sin(2\theta) = 1000\]

Answer

We will approximate the smallest positive solution in degrees, to two decimal places, to the range equation
\[45000\sin(2\theta) = 1000\]

Dividing both sides of the equation by \(45000\), we obtain \[\sin(2\theta) = \dfrac{1000}{45000} = \dfrac{1}{45}\]

So \[2\theta = \arcsin(\dfrac{1}{45})\]

\[\theta = \dfrac{1}{2}\arcsin(\dfrac{1}{45})\]

Using a calculator in degree mode, we obtain \(\theta \approx 0.64^\circ\).

We can also use the Double Angle Identities to solve equations with multiple angles.

Example \(\PageIndex{2}\): (Solving an Equation with a Double Angle Identity)

Consider the equation

\[\sin(2\theta) = \sin(\theta)\]

The fact that the two trigonometric functions have different periods makes this equation a little more difficult. We can use the Double Angle Identity for the sine to rewrite the equation as

\[2\sin(\theta)\cos(\theta) = \sin(\theta)\]

At this point we may be tempted to cancel the factor of \(\sin(\theta)\) from both sides, but we should resist that temptation because \(\sin(\theta)\) can be 0 and we can’t divide by 0. Instead, let’s put everything one one side and factor:

\[2\sin(\theta)\cos(\theta) = \sin(\theta)\]

\[2\sin(\theta)\cos(\theta) - \sin(\theta) = 0\]

\[\sin(\theta)(2\cos(\theta) - 1) = 0\]

Now we have a product that is equal to 0, so at least one of the factors must be 0. This yields the two equations

\[\sin(\theta) = 0\] or \[\cos(\theta) - 1 = 0\]

We solve each equation in turn. We know that \(\sin(\theta) = 0\) when \(\theta = \pi k\) for integers \(k\). Also, \(\cos(\theta) - 1 = 0\) implies \(\cos(\theta) = 1\), and this happens when \(\theta = 2\pi k\) for integers \(k\).

Notice that these solutions are a subset of the collection \(\pi k\) of solutions of \(\sin(\theta) = 0\). Thus, the solutions to \(\sin(2\theta) = \sin(\theta)\) are \(\theta = \pi k\) for integers \(k\), as illustrated in Figure 4.10.

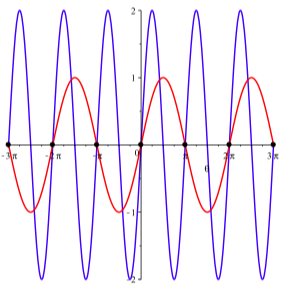
Figure \(\PageIndex{2}\): Graphs of \(y = \sin(2\theta)\) and \(y = \sin(\theta)\)

Exercise \(\PageIndex{4}\)

The goal is to solve the equation \(\cos(2\theta) = \sin(\theta)\).

1. Use a double angle identity to help rewrite the equation in the form \[2\sin^{2}(\theta) + \sin(\theta) - 1 = 0\]
2. Solve the quadratic type equation in (1) by factoring the left side of the equation.

Answer

1. We use the double angle identity \(\cos(2\theta) = 1 - 2\sin^{2}(\theta)\) to obtain

\[1 - 2\sin^{2}(\theta) = \sin(\theta)\]

\[1 - 2\sin^{2}(\theta) - \sin(\theta) = 0\]

\[2\sin^{2}(\theta) + \sin(\theta) - 1 = 0\]

2. Factoring gives \(2(\sin(\theta) - 1)(\sin(\theta) + 1) = 0\). Setting each factor equal to \(0\) and solving for \(\sin(\theta)\), we obtain

\[\sin(\theta) = \dfrac{1}{2}\] or \[\sin(\theta) = -1\]

So we have

\[\theta = \dfrac{\pi}{6} + k(2\pi)\] or \[\theta = \dfrac{5\pi}{6} + k(2\pi)\] or \[\theta = -\pi + k(2\pi)\]

where \(k\) is an integer.

Half Angle Identities

Now we investigate the half angle identities, identities for \(\cos(\dfrac{A}{2})\) and \(\sin(\dfrac{A}{2})\).

Here we use the double angle identities from Exercise \(\PageIndex{4}\):

\[\cos(A) = \cos(2(\dfrac{A}{2}))\]

\[\cos(A) = 2\cos^{2}(\dfrac{A}{2}) - 1\]
\[\cos(A) + 1 = 2\cos^{2}(\dfrac{A}{2})\]
\[\cos^{2}(\dfrac{A}{2}) = \dfrac{\cos(A) + 1}{2}\]
\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]

The sign of \(\cos(\dfrac{A}{2})\) depends on the quadrant in which \(\dfrac{A}{2}\) lies.

Example \(\PageIndex{3}\): (Using the Cosine Half Angle Identity)

We can use the Cosine Half Angle Identity to determine the exact value of \(\cos(\dfrac{7\pi}{12})\).

If we let \(A = \dfrac{7\pi}{6}\), then we have \(\dfrac{7\pi}{12} = \dfrac{A}{2}\). The Cosine Half Angle Identity shows us that

\[\cos(\dfrac{7\pi}{12}) = \cos(\dfrac{\dfrac{7\pi}{6}}{2}) = \pm\sqrt{\dfrac{1 + \cos(\dfrac{7\pi}{6})}{2}} = \pm\sqrt{\dfrac{1 - \dfrac{\sqrt{3}}{2}}{2}} = \pm\sqrt{\dfrac{2 - \sqrt{3}}{4}}\]

Since the terminal side of the angle \(\dfrac{7\pi}{12}\) lies in the second quadrant, we know that \(\cos(\dfrac{7\pi}{12})\) is negative. Therefore,

\[\cos(\dfrac{7\pi}{12}) = -\sqrt{\dfrac{2 - \sqrt{3}}{4}}.\]

We can find a similar half angle formula for the sine using the same approach:

\[\cos(A) = \cos(2(\dfrac{A}{2}))\]

\[\cos(A) = 1 - 2\sin^{2}(\dfrac{A}{2})\]
\[\cos(A) - 1 = 2\sin^{2}(\dfrac{A}{2})\]
\[\sin^{2}(\dfrac{A}{2}) = \dfrac{1 - \cos(A)}{2}\]
\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]

Again, the sign of \(\sin(\dfrac{A}{2})\) depends on the quadrant in which \(A\) lies.

Half Angle Identities

To summarize,

For any number \(A\) we have

\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]

\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]

where the sign depends on the quadrant in which \(\dfrac{A}{2}\) lies.

Exercise \(\PageIndex{5}\)

Use a Half Angle Identity to find the exact value of \(\cos(\dfrac{\pi}{8})\).

Answer

To determine the exact value of \(\cos(\dfrac{\pi}{8})\), we use the Half Angle Identity for cosine with \(A = \dfrac{\pi}{4}\).

\[\cos(\dfrac{\pi}{8}) = \pm\sqrt{\dfrac{1 + \cos(\dfrac{\pi}{4})}{2}} = \pm\sqrt{\dfrac{1 + \dfrac{\sqrt{2}}{2}}{2}}\]

Since \(\dfrac{\pi}{8}\) is in the first quadrant, we will use the positive square root. We can also rewrite the expression under the square root sign to obtain

\[\cos(\dfrac{\pi}{8}) =\sqrt{\dfrac{1 + \dfrac{\sqrt{2}}{2}}{2}} = \sqrt{\dfrac{\dfrac{2 + \sqrt{2}}{2}}{2}} = \sqrt{\dfrac{2 + \sqrt{2}}{4}} = \dfrac{\sqrt{2 + \sqrt{2}}}{2}\]

This result can be checked using a calculator.

Summary

In this section, we studied the following important concepts and ideas:

Double Angle Identities

\[\cos(2A) = \cos^{2}(A) - \sin^{2}(A)\]
\[\cos(2A) = 2\cos^{2}(A) - 1\]
\[\cos(2A) = 1 - 2\sin^{2}(A)\]
\[\sin(2A) = 2\cos(A)\sin(A)\]
\[\tan(2A) = \dfrac{2\tan(A)}{1 - \tan^{2}(A)}\]

Half Angle Identities

\[\cos(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 + \cos(A)}{2}}\]

\[\sin(\dfrac{A}{2}) = \pm\sqrt{\dfrac{1 - \cos(A)}{2}}\]

where the sign depends on the quadrant in which \(\dfrac{A}{2}\) lies.