5.2: The Trigonometric Form of a Complex Number
- Page ID
- 7125
Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- What is the polar (trigonometric) form of a complex number?
- How do we multiply two complex numbers in polar form?
- How do we divide one complex number in polar form by a nonzero complex number in polar form?
Beginning Activity
If \(z = a + bi\) is a complex number, then we can plot \(z\) in the plane as shown in Figure \(\PageIndex{1}\). In this situation, we will let \(r\) be the magnitude of \(z\) (that is, the distance from \(z\) to the origin) and \(\theta\) the angle \(z\) makes with the positive real axis as shown in Figure \(\PageIndex{1}\).
Use right triangle trigonometry to write \(a\) and \(b\) in terms of \(r\) and \(\theta\).
Explain why we can write \(z\) as
\[z = r(\cos(\theta) + i\sin(\theta)). \]
When we write \(z\) in the form given in Equation \(\PageIndex{1}\):, we say that \(z\) is written in trigonometric form (or polar form).
The angle \(\theta\) is called the argument of the argument of the complex number \(z\) and the real number \(r\) is the modulus or norm of \(z\). To find the polar representation of a complex number \(z = a + bi\), we first notice that
\[r = |z| = \sqrt{a^{2} + b^{2}}\]
\[a = r\cos(\theta)\]
\[b = r\sin(\theta)\]
Multiplication of complex numbers is more complicated than addition of complex numbers. To better understand the product of complex numbers, we first investigate the trigonometric (or polar) form of a complex number. This trigonometric form connects algebra to trigonometry and will be useful for quickly and easily finding powers and roots of complex numbers.
Note
The word polar here comes from the fact that this process can be viewed as occurring with polar coordinates.
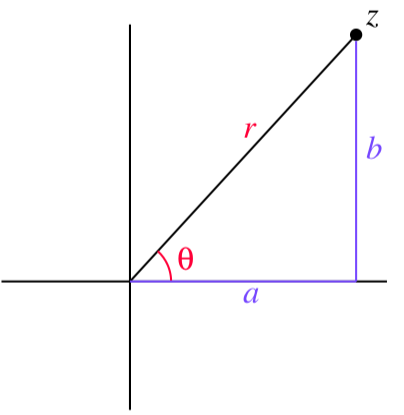
Figure \(\PageIndex{1}\): Trigonometric form of a complex number.
To find \(\theta\), we have to consider cases.
- If \(z = 0 = 0 + 0i\),then \(r = 0\) and \(\theta\) can have any real value.
- If \(z \neq 0\) and \(a \neq 0\), then \(\tan(\theta) = \dfrac{b}{a}\).
- If \(z \neq 0\) and \(a = 0\) (so \(b \neq 0\)), then
\[^* \space \theta = \dfrac{\pi}{2} \space if \space b > 0\]
\[^* \space \theta = -\dfrac{\pi}{2} \space if \space b < 0\]
Exercise \(\PageIndex{1}\)
- Determine the polar form of the complex numbers \(w = 4 + 4\sqrt{3}i\) and \(z = 1 - i\).
- Determine real numbers \(a\) and \(b\) so that \(a + bi = 3(\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6}))\)
- Answer
-
1. Note that \(|w| = \sqrt{4^{2} + (4\sqrt{3})^{2}} = 4\sqrt{4} = 8\) and the argument of \(w\) is \(\arctan(\dfrac{4\sqrt{3}}{4}) = \arctan\sqrt{3} = \dfrac{\pi}{3}\). So
\[w = 8(\cos(\dfrac{\pi}{3}) + \sin(\dfrac{\pi}{3}))\]
Also, \(|z| = \sqrt{1^{2} + 1^{2}} = \sqrt{2}\) and the argument of \(z\) is \(\arctan(\dfrac{-1}{1}) = -\dfrac{\pi}{4}\).
So \[z = \sqrt{2}(\cos(-\dfrac{\pi}{4}) + \sin(-\dfrac{\pi}{4})) = \sqrt{2}(\cos(\dfrac{\pi}{4}) - \sin(\dfrac{\pi}{4})\]
2. Recall that \(\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2}\) and \(\sin(\dfrac{\pi}{6}) = \dfrac{1}{2}\). So \[3(\cos(\dfrac{\pi}{6} + i\sin(\dfrac{\pi}{6})) = 3(\dfrac{\sqrt{3}}{2} + \dfrac{1}{2}i) = \dfrac{3\sqrt{3}}{2} + \dfrac{3}{2}i\]
So \(a = \dfrac{3\sqrt{3}}{2}\) and \(b = \dfrac{3}{2}\).
There is an alternate representation that you will often see for the polar form of a complex number using a complex exponential. We won’t go into the details, but only consider this as notation. When we write \(e^{i\theta}\) (where \(i\) is the complex number with \(i^{2} = -1\)) we mean
\[e^{i\theta} = \cos(\theta) + i\sin(\theta)\]
So the polar form \(r(\cos(\theta) + i\sin(\theta))\) can also be written as \(re^{i\theta}\):
\[re^{i\theta} = r(\cos(\theta) + i\sin(\theta))\]
Products of Complex Numbers in Polar Form
There is an important product formula for complex numbers that the polar form provides. We illustrate with an example.
Example \(\PageIndex{1}\): Products of Complex Numbers in Polar Form
Let \(w = -\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\) and \(z = \sqrt{3} + i\). Using our definition of the product of complex numbers we see that
\[wz = (\sqrt{3} + i)(-\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i) = -\sqrt{3} + i.\]
Now we write \(w\) and \(z\) in polar form. Note that \(|w| = \sqrt{(-\dfrac{1}{2})^{2} + (\dfrac{\sqrt{3}}{2})^{2}} = 1\) and the argument of \(w\) satisfies \(\tan(\theta) = -\sqrt{3}\). Since \(w\) is in the second quadrant, we see that \(\theta = \dfrac{2\pi}{3}\), so the polar form of \(w\) is \[w = \cos(\dfrac{2\pi}{3}) + i\sin(\dfrac{2\pi}{3})\]
Also, \(|z| = \sqrt{(\sqrt{3})^{2} + 1^{2}} = 2\) and the argument of \(z\) satisfies \(\tan(\theta) = \dfrac{1}{\sqrt{3}}\).
Since \(z\) is in the first quadrant, we know that \(\theta = \dfrac{\pi}{6}\) and the polar form of \(z\) is \[z = 2[\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6})]\]
We can also find the polar form of the complex product \(wz\). Here we have \(|wz| = 2\), and the argument of \(zw\) satisfies \(\tan(\theta) = -\dfrac{1}{\sqrt{3}}\). Since \(wz\) is in quadrant II, we see that \(\theta = \dfrac{5\pi}{6}\) and the polar form of \(wz\) is \[wz = 2[\cos(\dfrac{5\pi}{6}) + i\sin(\dfrac{5\pi}{6})].\]
When we compare the polar forms of \(w, z\), and \(wz\) we might notice that \(|wz| = |w||z|\) and that the argument of \(zw\) is \(\dfrac{2\pi}{3} + \dfrac{\pi}{6}\) or the sum of the arguments of \(w\) and \(z\). This turns out to be true in general.
The result of Example \(\PageIndex{1}\) is no coincidence, as we will show. In general, we have the following important result about the product of two complex numbers.
Multiplication of Complex Numbers in Polar Form
Let \(w = r(\cos(\alpha) + i\sin(\alpha))\) and \(z = s(\cos(\beta) + i\sin(\beta))\) be complex numbers in polar form. Then the polar form of the complex product \(wz\) is given by
\[wz = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\]
This states that to multiply two complex numbers in polar form, we multiply their norms and add their arguments.
To understand why this result it true in general, let \(w = r(\cos(\alpha) + i\sin(\alpha))\) and \(z = s(\cos(\beta) + i\sin(\beta))\) be complex numbers in polar form. We will use cosine and sine of sums of angles identities to find \(wz\):
\[w = [r(\cos(\alpha) + i\sin(\alpha))][s(\cos(\beta) + i\sin(\beta))] = rs([\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)]) + i[\cos(\alpha)\sin(\beta) + \cos(\beta)\sin(\alpha)]\]
We now use the cosine and sum identities and see that
\(\cos(\alpha + \beta) = \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)\) and \(\sin(\alpha + \beta) = \cos(\alpha)\sin(\beta) + \cos(\beta)\sin(\alpha)\).
Using equation (1) and these identities, we see that
\[w = rs([\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)]) + i[\cos(\alpha)\sin(\beta) + \cos(\beta)\sin(\alpha)] = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\]
An illustration of this is given in Figure \(\PageIndex{2}\). The formula for multiplying complex numbers in polar form tells us that to multiply two complex numbers, we add their arguments and multiply their norms.
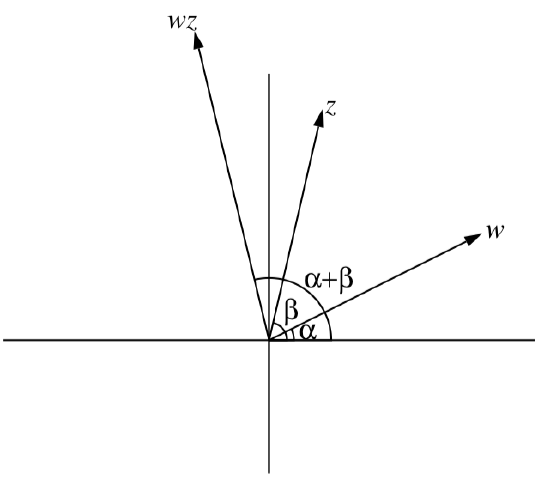
Figure \(\PageIndex{2}\): A Geometric Interpretation of Multiplication of Complex Numbers.
Exercise \(\PageIndex{2}\)
Let \(w = 3[\cos(\dfrac{5\pi}{3}) + i\sin(\dfrac{5\pi}{3})]\) and \(z = 2[\cos(-\dfrac{\pi}{4}) + i\sin(-\dfrac{\pi}{4})]\).
- What is \(|wz|\)?
- What is the argument of \(wz\)?
- In which quadrant is \(wz\)? Explain.
- Determine the polar form of wz.
- Draw a picture of \(w\), \(z\), and \(wz\) that illustrates the action of the complex product.
- Answer
-
1. Since \(|w| = 3\) and \(|z| = 2\), we see that
\[|wz| = |w||z| = (3)(2) = 6\]
2. The argument of \(w\) is \(\dfrac{5\pi}{3}\) and the argument of \(z\) is \(-\dfrac{\pi}{4}\), we see that the argument of \(wz\) is \[\dfrac{5\pi}{3} - \dfrac{\pi}{4} = \dfrac{20\pi - 3\pi}{12} = \dfrac{17\pi}{12}\]
3. The terminal side of an angle of \(\dfrac{17\pi}{12} = \pi + \dfrac{5\pi}{12}\) radians is in the third quadrant.
4. We know the magnitude and argument of \(wz\), so the polar form of \(wz\) is
\[wz = 6[\cos(\dfrac{17\pi}{12}) + \sin(\dfrac{17\pi}{12})]\]
5. Following is a picture of \(w, z\), and \(wz\) that illustrates the action of the complex product.
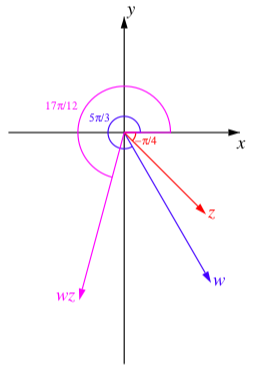
Quotients of Complex Numbers in Polar Form
We have seen that we multiply complex numbers in polar form by multiplying their norms and adding their arguments. There is a similar method to divide one complex number in polar form by another complex number in polar form.
Division of Complex Numbers in Polar Form
Let \(w = r(\cos(\alpha) + i\sin(\alpha))\) and \(z = s(\cos(\beta) + i\sin(\beta))\) be complex numbers in polar form with \(z \neq 0\). Then the polar form of the complex quotient \(\dfrac{w}{z}\) is given by \[\dfrac{w}{z} = \dfrac{r}{s}(\cos(\alpha - \beta) + i\sin(\alpha - \beta)).\]
So to divide complex numbers in polar form, we divide the norm of the complex number in the numerator by the norm of the complex number in the denominator and subtract the argument of the complex number in the denominator from the argument of the complex number in the numerator.
The proof of this is similar to the proof for multiplying complex numbers and is included as a supplement to this section.
Exercise \(\PageIndex{3}\)
Let \(w = 3[\cos(\dfrac{5\pi}{3}) + i\sin(\dfrac{5\pi}{3})]\) and \(z = 2[\cos(-\dfrac{\pi}{4}) + i\sin(-\dfrac{\pi}{4})]\).
- What is \(|\dfrac{w}{z}|\)?
- What is the argument of \(|\dfrac{w}{z}|\)?
- In which quadrant is \(|\dfrac{w}{z}|\)? Explain.
- Determine the polar form of \(|\dfrac{w}{z}|\).
- Draw a picture of \(w\), \(z\), and \(|\dfrac{w}{z}|\) that illustrates the action of the complex product.
- Answer
-
1. Since \(|w| = 3\) and \(|z| = 2\), we see that
\[|\dfrac{w}{z}| = \dfrac{|w|}{|z|} = \dfrac{3}{2}\]
2. The argument of \(w\) is \(\dfrac{5\pi}{3}\) and the argument of \(z\) is \(-\dfrac{\pi}{4}\), we see that the argument of \(\dfrac{w}{z}\) is
\[\dfrac{5\pi}{3} - (-\dfrac{\pi}{4}) = \dfrac{20\pi + 3\pi}{12} = \dfrac{23\pi}{12}\]
3. The terminal side of an angle of \(\dfrac{23\pi}{12} = 2\pi - \dfrac{\pi}{12}\) radians is in the fourth quadrant.
4. We know the magnitude and argument of \(wz\), so the polar form of \(wz\) is \[\dfrac{w}{z} = \dfrac{3}{2}[\cos(\dfrac{23\pi}{12}) + \sin(\dfrac{23\pi}{12})]\]
5. Following is a picture of \(w, z\), and \(wz\) that illustrates the action of the complex product.
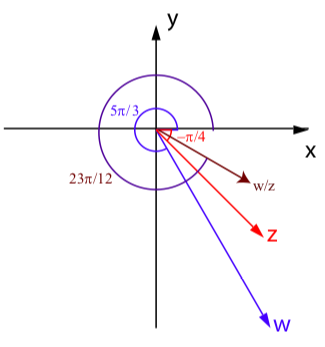
Proof of the Rule for Dividing Complex Numbers in Polar Form
Let \(w = r(\cos(\alpha) + i\sin(\alpha))\) and \(z = s(\cos(\beta) + i\sin(\beta))\) be complex numbers in polar form with \(z \neq 0\). So
\[\dfrac{w}{z} = \dfrac{r(\cos(\alpha) + i\sin(\alpha))}{s(\cos(\beta) + i\sin(\beta)} = \dfrac{r}{s}\left [\dfrac{\cos(\alpha) + i\sin(\alpha)}{\cos(\beta) + i\sin(\beta)} \right ]\]
We will work with the fraction \(\dfrac{\cos(\alpha) + i\sin(\alpha)}{\cos(\beta) + i\sin(\beta)}\) and follow the usual practice of multiplying the numerator and denominator by \(\cos(\beta) - i\sin(\beta)\). So
\[\dfrac{w}{z} = \dfrac{r}{s}\left [\dfrac{(\cos(\alpha) + i\sin(\alpha))}{(\cos(\beta) + i\sin(\beta)} \right ] = \dfrac{r}{s}\left [\dfrac{(\cos(\alpha) + i\sin(\alpha))}{(\cos(\beta) + i\sin(\beta)} \cdot \dfrac{(\cos(\beta) - i\sin(\beta))}{(\cos(\beta) - i\sin(\beta)} \right ] = \dfrac{r}{s}\left [\dfrac{(\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)) + i(\sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta)}{\cos^{2}(\beta) + \sin^{2}(\beta)} \right ]\]
We now use the following identities with the last equation:
- \(\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta) = \cos(\alpha - \beta)\)
- \(\sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta) = \sin(\alpha - \beta)\)
- \(\cos^{2}(\beta) + \sin^{2}(\beta) = 1\)
Using these identities with the last equation for \(\dfrac{w}{z}\), we see that
\[\dfrac{w}{z} = \dfrac{r}{s}[\dfrac{\cos(\alpha - \beta) + i\sin(\alpha- \beta)}{1}].\]
Summary
In this section, we studied the following important concepts and ideas:
If \(z = a + bi\) is a complex number, then we can plot \(z\) in the plane. If \(r\) is the magnitude of \(z\) (that is, the distance from \(z\) to the origin) and \(\theta\) the angle \(z\) makes with the positive real axis, then the trigonometric form (or polar form) of \(z\) is \(z = r(\cos(\theta) + i\sin(\theta))\), where
\[r = \sqrt{a^{2} + b^{2}}, \cos(\theta) = \dfrac{a}{r}\]
and \[\sin(\theta) = \dfrac{b}{r}\]
The angle \(\theta\) is called the argument of the complex number \(z\) and the real number \(r\) is the modulus or norm of \(z\).
If \(w = r(\cos(\alpha) + i\sin(\alpha))\) and \(z = s(\cos(\beta) + i\sin(\beta))\) are complex numbers in polar form, then the polar form of the complex product \(wz\) is given by
\[wz = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\] and \(z \neq 0\), the polar form of the complex quotient \(\dfrac{w}{z}\) is
\[\dfrac{w}{z} = \dfrac{r}{s}(\cos(\alpha - \beta) + i\sin(\alpha - \beta)),\]
This states that to multiply two complex numbers in polar form, we multiply their norms and add their arguments, and to divide two complex numbers, we divide their norms and subtract their arguments.


