2.3: The Law of Tangents
- Page ID
- 3256
We have shown how to solve a triangle in all four cases discussed at the beginning of this chapter. An alternative to the Law of Cosines for Case 3 (two sides and the included angle) is the Law of Tangents:
If a triangle has sides of lengths \(a \), \(b \), and \(c \) opposite the angles \(A \), \(B \), and \(C \), respectively, then
\[ \begin{align}
\label{2.17}\frac{a-b}{a+b} ~&=~
\frac{\tan\;\frac{1}{2}(A-B)}{\tan\;\frac{1}{2}(A+B)} ~,\\ \label{2.18}
\frac{b-c}{b+c} ~&=~
\frac{\tan\;\frac{1}{2}(B-C)}{\tan\;\frac{1}{2}(B+C)} ~,\\ \label{2.19}
\frac{c-a}{c+a} ~&=~
\frac{\tan\;\frac{1}{2}(C-A)}{\tan\;\frac{1}{2}(C+A)} ~. \\
\end{align} \]
Note that since \(\tan\;(-\theta) = -\tan\;\theta \) for any angle \(\theta \), we can switch the order of the letters in each of the above formulas. For example, we can rewrite Equation \ref{2.17} as
\[\label{2.20}
\frac{b-a}{b+a}~=~\frac{\tan\;\frac{1}{2}(B-A)}{\tan\;\frac{1}{2}(B+A)}~,
\]
and similarly for the other formulas. If \(a > b \), then it is usually more convenient to use Equation \ref{2.17}, while Equation \ref{2.20} is more convenient when \(b > a \).
Solve the triangle \(\triangle\,ABC \) given \(a =5 \), \(b = 3 \), and \(C = 96^\circ \).
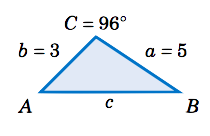
Solution
\(A + B + C = 180^\circ \), so \(A + B = 180^\circ - C = 180^\circ - 96^\circ = 84^\circ \). Thus, by the Law of Tangents,
\[\nonumber \begin{align*}
\frac{a-b}{a+b} ~=~ \frac{\tan\;\frac{1}{2}(A-B)}{\tan\;\frac{1}{2}(A+B)} \quad&\Rightarrow\quad
\frac{5-3}{5+3} ~=~ \frac{\tan\;\frac{1}{2}(A-B)}{\tan\;\frac{1}{2}(84^\circ)}\\ \nonumber
&\Rightarrow\quad \tan\;\tfrac{1}{2}(A-B) ~=~ \tfrac{2}{8}\tan\;42^\circ ~=~ 0.2251\\ \nonumber
&\Rightarrow\quad \tfrac{1}{2}(A-B) ~=~ 12.7^\circ \quad\Rightarrow\quad A-B ~=~ 25.4^\circ ~. \\
\end{align*}\]
We now have two equations involving \(A \) and \(B \), which we can solve by adding the equations:
\[\nonumber \begin{alignat*}{3}
A &- B &&=\; 25.4^\circ\\ \nonumber
A &+ B &&=\; 84^\circ\phantom{4^\circ}\\[-2mm] \nonumber
--&--&&----\\[-2mm] \nonumber
2A &\phantom{+} &&=\; 109.4^\circ \quad\Rightarrow\quad \boxed{A = 54.7^\circ}
\quad\Rightarrow\quad B ~=~ 84^\circ - 54.7^\circ \quad\Rightarrow\quad
\boxed{B = 29.3^\circ} \\
\end{alignat*} \nonumber \]
We can find the remaining side \(c \) by using the Law of Sines:
\[ c ~=~ \frac{a\;\sin\;C}{\sin\;A} ~=~ \frac{5\;\sin\;96^\circ}{\sin\;54.7^\circ}
\quad\Rightarrow\quad \boxed{c = 6.09} \nonumber \]
Note that in any triangle \(\triangle\,ABC \), if \(a = b \) then \(A = B \) (why?), and so both sides of Equation \ref{2.17} would be \(0 \) (since \(\tan\;0^\circ = 0\)). This means that the Law of Tangents is of no help in Case 3 when the two known sides are equal. For this reason, and perhaps also because of the somewhat unusual way in which it is used, the Law of Tangents seems to have fallen out of favor in trigonometry books lately. It does not seem to have any advantages over the Law of Cosines, which works even when the sides are equal, requires slightly fewer steps, and is perhaps more straightforward.
Related to the Law of Tangents are Mollweide's equations:
For any triangle \(\triangle\,ABC \),
\[\begin{align}
\frac{a-b}{c} ~&=~
\frac{\sin\;\frac{1}{2}(A-B)}{\cos\;\frac{1}{2}C} ~,~\text{and}\label{2.21}\\[4pt]
\frac{a+b}{c} ~&=~
\frac{\cos\;\frac{1}{2}(A-B)}{\sin\;\frac{1}{2}C} ~.\label{2.22}
\end{align} \]
Note that all six parts of a triangle appear in both of Mollweide's equations. For this reason, either equation can be used to check a solution of a triangle. If both sides of the equation agree (more or less), then we know that the solution is correct.
Use one of Mollweide's equations to check the solution of the triangle from Example 2.10.
Solution
Recall that the full solution was \(a=5 \), \(b=3 \), \(c=6.09 \), \(A=54.7^\circ \), \(B=29.3^\circ \), and \(C=96^\circ \). We will check this with Equation \ref{2.21}:
\[\begin{align*}
\frac{a-b}{c} ~&=~ \frac{\sin\;\frac{1}{2}(A-B)}{\cos\;\frac{1}{2}C}\\ \nonumber
\frac{5-3}{6.09} ~&=~
\frac{\sin\;\frac{1}{2}(54.7^\circ - 29.3^\circ)}{\cos\;\frac{1}{2}(96^\circ)}\\ \nonumber
\frac{2}{6.09} ~&=~ \frac{\sin\;12.7^\circ}{\cos\;48^\circ}\\ \nonumber
0.3284 ~&=~ 0.3285 \quad \checkmark
\end{align*} \]
The small difference (\(\approx 0.0001\)) is due to rounding errors from the original solution, so we can conclude that both sides of the equation agree, and hence the solution is correct.
Can a triangle have the parts \(a=6 \), \(b=7 \), \(c=9 \), \(A=55^\circ \), \(B=60^\circ \), and \(C=65^\circ\;\)?
Solution
Before using Mollweide's equations, simpler checks are that the angles add up to \(180^\circ \) and that the smallest and largest sides are opposite the smallest and largest angles, respectively. In this case all those conditions hold. So check with Mollweide's Equation \ref{2.22}:
\[\nonumber \begin{align*}
\frac{a+b}{c} ~&=~ \frac{\cos\;\frac{1}{2}(A-B)}{\sin\;\frac{1}{2}C}\\ \nonumber
\frac{6+7}{9} ~&=~
\frac{\cos\;\frac{1}{2}(55^\circ - 60^\circ)}{\sin\;\frac{1}{2}(65^\circ)}\\ \nonumber
\frac{13}{9} ~&=~ \frac{\cos\;(-2.5^\circ)}{\sin\;32.5^\circ}\\ \nonumber
1.44 ~&=~ 1.86 \quad\times
\end{align*} \nonumber \]
Here the difference is far too large, so we conclude that there is no triangle with these parts.
We will prove the Law of Tangents and Mollweide's equations in Chapter 3, where we will be able to supply brief analytic proofs.


