3.2: Sum and Difference Formulas
- Page ID
- 3286
We will now derive identities for the trigonometric functions of the sum and difference of two angles. For the sum of any two angles \(A \) and \(B \), we have the addition formulas:
\[\sin\;(A+B) ~=~ \sin\;A ~ \cos\;B ~+~ \cos\;A ~ \sin\;B\label{eqn:sumsin} \]
\[ \cos\;(A+B) ~=~ \cos\;A ~ \cos\;B ~-~ \sin\;A ~ \sin\;B\label{eqn:sumcos} \]
To prove these, first assume that \(A \) and \(B \) are acute angles. Then \(A+B \) is either acute or obtuse, as in Figure 3.2.1. Note in both cases that \(\angle\,QPR = A \), since
\[ \begin{align*}
\angle\,QPR ~&=~ \angle\,QPO - \angle\,OPM ~=~ (90^\circ - B) -
(90^\circ - (A+B)) ~=~ A ~~\text{in Figure 3.2.1(a), and}\\[4pt]
\angle\,QPR ~&=~ \angle\,QPO + \angle\,OPM ~=~ (90^\circ - B) +
(90^\circ - (180^\circ - (A+B))) ~=~ A ~~\text{in Figure 3.2.1(b).}
\end{align*} \nonumber \]
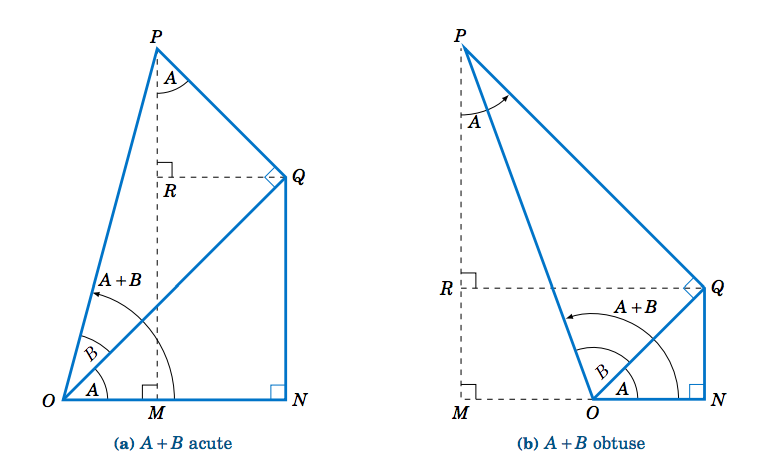
Thus,
\[ \begin{align*}
\sin\;(A+B) ~&=~ \frac{MP}{OP} ~=~ \frac{MR+RP}{OP} ~=~ \frac{NQ+RP}{OP} ~=~
\frac{NQ}{OP} ~+~ \frac{RP}{OP} \\[4pt]
&=~ \frac{NQ}{OQ}\,\cdot\,\frac{OQ}{OP} ~+~ \frac{RP}{PQ}\,\cdot\,\frac{PQ}{OP}\nonumber\\[4pt]
&=~ \sin\;A ~ \cos\;B ~+~ \cos\;A ~ \sin\;B ~,\label{eqn:sinsumproof}
\end{align*} \nonumber \]
and
\[ \begin{align*}
\cos\;(A+B) ~&=~ \frac{OM}{OP} ~=~ \frac{ON-MN}{OP} ~=~ \frac{ON-RQ}{OP} ~=~
\frac{ON}{OP} ~-~ \frac{RQ}{OP} \\[4pt]
&=~ \frac{ON}{OQ}\,\cdot\,\frac{OQ}{OP} ~-~ \frac{RQ}{PQ}\,\cdot\,\frac{PQ}{OP} \\[4pt]
&=~ \cos\;A ~ \cos\;B ~-~ \sin\;A ~ \sin\;B ~.\label{eqn:cossumproof}
\end{align*} \nonumber \]
So we have proved the identities for acute angles \(A \) and \(B \). It is simple to verify that they hold in the special case of \(A=B=0^\circ \). For general angles, we will need to use the relations we derived in Section 1.5 which involve adding or subtracting \(90^\circ\):
\[ \begin{alignat*}{4}
\sin\;(\theta + 90^\circ) ~ &= ~ \phantom{-}\cos\;\theta &\qquad\quad
\sin\;(\theta - 90^\circ) ~ &= ~ -\cos\;\theta\\[4pt]
\cos\;(\theta + 90^\circ) ~ &= ~ -\sin\;\theta &\qquad\quad
\cos\;(\theta - 90^\circ) ~ &= ~ \phantom{-}\sin\;\theta
\end{alignat*} \nonumber \]
These will be useful because any angle can be written as the sum of an acute angle (or \(0^\circ\)) and integer multiples of \(\pm 90^\circ\). For example, \(155^\circ = 65^\circ + 90^\circ \), \(222^\circ = 42^\circ + 2(90^\circ) \), \(-77^\circ = 13^\circ - 90^\circ \), etc. So if we can prove that the identities hold when adding or subtracting \(90^\circ \) to or from either \(A\) or \(B \), respectively, where \(A \) and \(B \) are acute or \(0^\circ \), then the identities will also hold when repeatedly adding or subtracting \(90^\circ \), and hence will hold for all angles. Replacing \(A \) by \(A+90^\circ \) and using the relations for adding \(90^\circ \) gives
\[ \begin{align*}
\sin\;((A+90^\circ) + B) ~&=~ \sin\;((A+B) + 90^\circ) ~=~ \cos\;(A+B)~,\\[4pt]
&=~ \cos\;A ~ \cos\;B ~-~ \sin\;A ~ \sin\;B ~~\text{(by Equation \ref{eqn:cossumproof})}\\[4pt]
&=~ \sin\;(A + 90^\circ)~\cos\;B ~+~ \cos\;(A + 90^\circ)~\sin\;B ~,\end{align*} \nonumber \]
so the identity holds for \(A+90^\circ \) and \(B \) (and, similarly, for \(A \) and \(B+90^\circ\)). Likewise,
\[ \nonumber \begin{align*} \sin\;((A-90^\circ) + B) ~&=~ \sin\;((A+B) - 90^\circ) ~=~ -\cos\;(A+B)~,\\[4pt]
&=~ -(\cos\;A ~ \cos\;B ~-~ \sin\;A ~ \sin\;B) \\[4pt]
&=~ (-\cos\;A) ~ \cos\;B ~+~ \sin\;A ~ \sin\;B\\[4pt]
&=~ \sin\;(A - 90^\circ)~\cos\;B ~+~ \cos\;(A - 90^\circ)~\sin\;B ~,
\end{align*} \nonumber \]
so the identity holds for \(A-90^\circ \) and \(B \) (and, similarly, for \(A \) and \(B+90^\circ\)). Thus, the addition Equation \ref{eqn:sumsin} for sine holds for all \(A \) and \(B \). A similar argument shows that the addition Equation \ref{eqn:sumcos} for cosine is true for all \(A \) and \(B \). QED
Replacing \(B \) by \(-B \) in the addition formulas and using the relations \(\sin\;(-\theta) = -\sin\;\theta \) and \(\cos\;(-\theta) = \cos\;\theta \) from Section 1.5 gives us the subtraction formulas:
\[ \sin\;(A-B) ~=~ \sin\;A ~ \cos\;B ~-~ \cos\;A ~ \sin\;B\label{eqn:diffsin} \]
\[ \cos\;(A-B) ~=~ \cos\;A ~ \cos\;B ~+~ \sin\;A ~ \sin\;B\label{eqn:diffcos} \]
Using the identity \(\tan\;\theta = \frac{\sin\;\theta}{\cos\;\theta} \), and the addition formulas for sine and cosine, we can derive the addition formula for tangent:
\[\require{cancel} \begin{align*}
\tan\;(A+B) ~&=~ \frac{\sin\;(A+B)}{\cos\;(A+B)}\\[4pt]
&=~ \frac{\sin\;A ~ \cos\;B ~+~ \cos\;A ~ \sin\;B}{\cos\;A ~ \cos\;B ~-~ \sin\;A ~ \sin\;B}\\[4pt]
&=~ \frac{\dfrac{\sin\;A ~ \cos\;B}{\cos\;A ~ \cos\;B} ~+~
\dfrac{\cos\;A ~ \sin\;B}{\cos\;A ~ \cos\;B}}{\dfrac{\cos\;A ~ \cos\;B}{\cos\;A ~ \cos\;B}
~-~ \dfrac{\sin\;A ~ \sin\;B}{\cos\;A ~ \cos\;B}}\quad\text{(divide top and bottom by
\(\cos\;A ~ \cos\;B\))}\\[4pt]
&=~ \frac{\dfrac{\sin\;A}{\cos\;A} \;\cdot\; \cancel{\dfrac{\cos\;B}{\cos\;B}} ~+~
\cancel{\dfrac{\cos\;A}{\cos\;A}} \;\cdot\; \dfrac{\sin\;B}{\cos\;B}}{1 ~-~
\dfrac{\sin\;A}{\cos\;A} \;\cdot\; \dfrac{\sin\;B}{\cos\;B}}\\[4pt]
&=~ \frac{\tan\;A ~+~ \tan\;B}{1 ~-~ \tan\;A ~ \tan\;B}
\end{align*} \nonumber \]
This, combined with replacing \(B \) by \(-B \) and using the relation \(\tan\;(-\theta) = -\tan\;\theta \), gives us the addition and subtraction formulas for tangent:
\[ \tan\;(A+B) ~=~ \frac{\tan\;A ~+~ \tan\;B}{1 ~-~ \tan\;A ~ \tan\;B}\label{eqn:sumtan} \]
\[\tan\;(A-B) ~=~ \frac{\tan\;A ~-~ \tan\;B}{1 ~+~ \tan\;A ~ \tan\;B}\label{eqn:difftan} \]
Given angles \(A \) and \(B \) such that \(\sin\;A = \frac{4}{5} \), \(\cos\;A = \frac{3}{5} \), \(\sin\;B = \frac{12}{13} \), and \(\cos\;B = \frac{5}{13} \), find the exact values of \(\sin\;(A+B) \), \(\cos\;(A+B) \), and \(\tan\;(A+B) \).
Solution
Using the addition formula for sine, we get:
\[ \begin{align*}
\sin\;(A+B) ~&=~ \sin\;A ~ \cos\;B ~+~ \cos\;A ~ \sin\;B\\[4pt]
&=~ \frac{4}{5} \;\cdot\; \frac{5}{13} ~+~ \frac{3}{5} \;\cdot\; \frac{12}{13}
\quad\Rightarrow\quad \boxed{\sin\;(A+B) ~=~ \frac{56}{65}} \end{align*} \nonumber \]
Using the addition formula for cosine, we get:
\[ \begin{align*}\cos\;(A+B) ~&=~ \cos\;A ~ \cos\;B ~-~ \sin\;A ~ \sin\;B\\[4pt]
&=~ \frac{3}{5} \;\cdot\; \frac{5}{13} ~-~ \frac{4}{5} \;\cdot\; \frac{12}{13}
\quad\Rightarrow\quad \boxed{\cos\;(A+B) ~=~ -\frac{33}{65}}\end{align*} \nonumber \]
Instead of using the addition formula for tangent, we can use the results above:
\[ \tan\;(A+B) ~=~ \frac{\sin\;(A+B)}{\cos\;(A+B)}
~=~ \frac{\frac{56}{65}}{-\frac{33}{65}}
\quad\Rightarrow\quad \boxed{\tan\;(A+B) ~=~ -\frac{56}{33}} \nonumber \]
Prove the following identity:
\[ \sin\;(A+B+C) ~=~ \sin\;A~\cos\;B~\cos\;C \;+\; \cos\;A~\sin\;B~\cos\;C \;+\;
\cos\;A~\cos\;B~\sin\;C \;-\; \sin\;A~\sin\;B~\sin\;C \nonumber \]
Solution
Treat \(A+B+C \) as \((A+B)+C \) and use the addition formulas three times:
\[ \begin{align*}
\sin\;(A+B+C) ~&=~ \sin\;((A+B)+C)\\[4pt]
&=~ \sin\;(A+B)~\cos\;C \;+\; \cos\;(A+B)~\sin\;C\\[4pt]
&=~ (\sin\;A ~ \cos\;B \;+\; \cos\;A ~ \sin\;B)~\cos\;C \;+\;
(\cos\;A ~ \cos\;B \;-\; \sin\;A ~ \sin\;B)~\sin\;C\\[4pt]
&=~ \sin\;A~\cos\;B~\cos\;C \;+\; \cos\;A~\sin\;B~\cos\;C \;+\;
\cos\;A~\cos\;B~\sin\;C \;-\; \sin\;A~\sin\;B~\sin\;C
\end{align*} \nonumber \]
For any triangle \(\triangle\,ABC \), show that \(\tan\;A + \tan\;B + \tan\;C =
\tan\;A~\tan\;B~\tan\;C \).
Solution
Note that this is not an identity which holds for all angles; since \(A \), \(B \), and \(C \) are the angles of a triangle, it holds when \(A \), \(B \), \(C\) \(> 0^\circ \) and \(A + B + C = 180^\circ \). So using \(C = 180^\circ - (A+B) \) and the relation \(\;\tan\;(180^\circ - \theta) = -\tan\;\theta\; \) from Section 1.5, we get:
\[ \begin{align*} \tan\;A \;+\; \tan\;B \;+\; \tan\;C ~&=~ \tan\;A \;+\; \tan\;B \;+\; \tan\;(180^\circ - (A+B))\\[4pt]
&=~ \tan\;A \;+\; \tan\;B \;-\; \tan\;(A+B)\\[4pt]
&=~ \tan\;A \;+\; \tan\;B \;-\; \frac{\tan\;A + \tan\;B}{1 - \tan\;A ~ \tan\;B} \\[4pt]
&=~ (\tan\;A \;+\; \tan\;B)~\left( 1 \;-\; \dfrac{1}{1 - \tan\;A ~ \tan\;B} \right) \\[4pt]
&=~ (\tan\;A \;+\; \tan\;B)~\left( \dfrac{1 - \tan\;A ~ \tan\;B}{1 - \tan\;A ~ \tan\;B} \;-\;
\dfrac{1}{1 - \tan\;A ~ \tan\;B} \right ) \\[4pt]
&=~ (\tan\;A \;+\; \tan\;B)\;\cdot\;\left ( \frac{-\tan\;A ~ \tan\;B}{1 - \tan\;A ~ \tan\;B}
\right ) \\[4pt]
&=~ \tan\;A ~ \tan\;B \;\cdot\; \left( -\frac{\tan\;A \;+\; \tan\;B}{1 - \tan\;A ~ \tan\;B} \right )\\[4pt]
&=~ \tan\;A ~ \tan\;B \;\cdot\; (-\tan\;(A+B))\\[4pt]
&=~ \tan\;A ~ \tan\;B \;\cdot\; (\tan\;(180^\circ - (A+B)))\\[4pt]
&=~ \tan\;A ~ \tan\;B ~ \tan\;C
\end{align*} \nonumber \]
Let \(A \), \(B \), \(C \), and \(D \) be positive angles such that \(A+B+C+D=180^\circ \). Show that
\[\sin\;A~\sin\;B ~+~ \sin\;C~\sin\;D ~=~ \sin\;(A+C)~\sin\;(B+C) ~. \nonumber \]
Solution
It may be tempting to expand the right side, since it appears more complicated. However, notice that the right side has no \(D \) term. So instead, we will expand the left side, since we can eliminate the \(D \) term on that side by using \(D=180^\circ - (A+B+C) \) and the relation
\[\sin\;(180^\circ -(A+B+C)) ~=~ \sin\;(A+B+C).\nonumber \]
So since \(\;\sin\;D = \sin\;(A+B+C) \), we get
\[ \begin{align*}
\sin\;A~\sin\;B ~+~ \sin\;C~\sin\;D ~&=~ \sin\;A~\sin\;B ~+~ \sin\;C~\sin\;(A+B+C) ~,~\text{so by Example 3.9 we get}\\[4pt]
&=~ \sin\;A~\sin\;B ~+~ \sin\;C~(\sin\;A~\cos\;B~\cos\;C \;+\; \cos\;A~\sin\;B~\cos\;C\\[4pt]
&\quad +\; \cos\;A~\cos\;B~\sin\;C \;-\; \sin\;A~\sin\;B~\sin\;C)\\[4pt]
&=~ \sin\;A~\sin\;B ~+~ \sin\;C~\sin\;A~\cos\;B~\cos\;C ~+~ \sin\;C~\cos\;A~\sin\;B~\cos\;C\\[4pt]
&\quad +~ \sin\;C~\cos\;A~\cos\;B~\sin\;C ~-~
\sin\;C~\sin\;A~\sin\;B~\sin\;C ~. \end{align*} \nonumber \]
It may not be immediately obvious where to go from here, but it is not completely guesswork. We need to end up with \(\sin\;(A+C)~\sin\;(B+C) \), and we know that \(\sin\;(B+C) = \sin\;B~\cos\;C + \cos\;B~\sin\;C \). There are two terms involving \(\;\cos\;B~\sin\;C \), so group them together to get
\[ \begin{align*} \sin\;A~\sin\;B ~+~ \sin\;C~\sin\;D ~
&=~ \sin\;A~\sin\;B ~-~ \sin\;C~\sin\;A~\sin\;B~\sin\;C ~+~ \sin\;C~\cos\;A~\sin\;B~\cos\;C\\[4pt]
&\quad+~ \cos\;B~\sin\;C~(\sin\;A~\cos\;C ~+~ \cos\;A~\sin\;C)\\[4pt]
&=~ \sin\;A~\sin\;B~(1 - \sin^2 \;C) ~+~ \sin\;C~\cos\;A~\sin\;B~\cos\;C\\[4pt]
&\quad +~ \cos\;B~\sin\;C~\sin\;(A+C)\\[4pt]
&=~ \sin\;A~\sin\;B~\cos^2 \;C ~+~ \sin\;C~\cos\;A~\sin\;B~\cos\;C\\[4pt]
&\quad +~ \cos\;B~\sin\;C~\sin\;(A+C)~. \end{align*} \nonumber \]
We now have two terms involving \(\;\sin\;B~\cos\;C \), which we can factor out:
\[\begin{align*} \sin\;A~\sin\;B ~+~ \sin\;C~\sin\;D ~&=~ \sin\;B~\cos\;C~(\sin\;A~\cos\;C + \cos\;A~\sin\;C~)\\[4pt]
&\quad +~ \cos\;B~\sin\;C~\sin\;(A+C)\\[4pt] &=~ \sin\;B~\cos\;C~\sin\;(A+C) ~+~ \cos\;B~\sin\;C~\sin\;(A+C)\\[4pt] &=~ \sin\;(A+C)~(\sin\;B~\cos\;C + \cos\;B~\sin\;C)\\[4pt] &=~ \sin\;(A+C)~\sin\;(B+C) \\[4pt]\end{align*} \nonumber \]
In the study of the propagation of electromagnetic waves, Snell's law gives the relation
\[n_1 ~\sin\;\theta_1 ~=~ n_2 ~\sin\;\theta_2\label{eqn:snell} ~, \]
where \(\theta_1 \) is the angle of incidence at which a wave strikes the planar boundary between two mediums, \(\theta_2 \) is the angle of transmission of the wave through the new medium, and \(n_1 \) and \(n_2\) are the indexes of refraction of the two mediums. The quantity
\[r_{1\;2\;s} ~=~ \frac{n_1 ~\cos\;\theta_1 ~-~ n_2 ~\cos\;\theta_2}{n_1 ~\cos\;\theta_1 ~+~
n_2 ~\cos\;\theta_2}\label{3.21} \]
is called the Fresnel coefficient for normal incidence reflection of the wave for s-polarization. Show that this can be written as:
\[ r_{1\;2\;s} ~=~ \frac{\sin\;(\theta_2 - \theta_1)}{\sin\;(\theta_2 + \theta_1)} \nonumber \]
Solution
Multiply the top and bottom of \(r_{1\;2\;s} \) by \(\;\sin\;\theta_1 ~ \sin\;\theta_2\; \) to get:
\[ \begin{align*}
r_{1\;2\;s} ~&=~ \frac{n_1 ~\cos\;\theta_1 ~-~ n_2 ~\cos\;\theta_2}{n_1 ~\cos\;\theta_1 ~+~
n_2 ~\cos\;\theta_2} \;\cdot\; \frac{\sin\;\theta_1 ~ \sin\;\theta_2}{\sin\;\theta_1 ~
\sin\;\theta_2}\\[4pt]
&=~ \frac{(n_1 ~\sin\;\theta_1)~\sin\;\theta_2 ~\cos\;\theta_1 ~-~
(n_2 ~\sin\;\theta_2)~\cos\;\theta_2 ~\sin\;\theta_1}{
(n_1 ~\sin\;\theta_1)~\sin\;\theta_2 ~\cos\;\theta_1 ~+~
(n_2 ~\sin\;\theta_2)~\cos\;\theta_2 ~\sin\;\theta_1}\\[4pt]
&=~ \frac{(n_1 ~\sin\;\theta_1)~\sin\;\theta_2 ~\cos\;\theta_1 ~-~
(n_1 ~\sin\;\theta_1)~\cos\;\theta_2 ~\sin\;\theta_1}{
(n_1 ~\sin\;\theta_1)~\sin\;\theta_2 ~\cos\;\theta_1 ~+~
(n_1 ~\sin\;\theta_1)~\cos\;\theta_2 ~\sin\;\theta_1}
\qquad\text{(by Snell's law)}\\[4pt]
&=~ \frac{\sin\;\theta_2 ~\cos\;\theta_1 ~-~
\cos\;\theta_2 ~\sin\;\theta_1}{
\sin\;\theta_2 ~\cos\;\theta_1 ~+~
\cos\;\theta_2 ~\sin\;\theta_1}\\[4pt]
&=~ \frac{\sin\;(\theta_2 - \theta_1)}{\sin\;(\theta_2 + \theta_1)}
\end{align*} \nonumber \]
The last two examples demonstrate an important aspect of how identities are used in practice: recognizing terms which are part of known identities, so that they can be factored out. This is a common technique.


